Table of Content
Important
Tham khảo
Levenshtein Distance
Khoảng cách chỉnh sửa văn bản Levenshtein
Bài toán: Viết chương trình tính khoảng cách chỉnh sửa tối thiểu Levenshtein. Khoảng cách Levenshtein thể hiện khoảng cách khác biệt giữa 2 chuỗi ký tự. Khoảng cách Levenshtein giữa chuỗi S và chuỗi T là số bước ít nhất biến chuỗi S thành chuỗi T thông qua 3 phép biến đổi là:
-
Xoá một ký tự
-
Thêm một ký tự
-
Thay thế ký tự này bằng ký tự khác Khoảng cách này được sử dụng trong việc tính toán sự giống và khác nhau giữa 2 chuỗi, như chương trình kiểm tra lỗi chính tả của winword spellchecker. Ví dụ: Khoảng cách Levenshtein giữa 2 chuỗi “kitten” và “sitting” là 3, vì phải dùng ít nhất 3 lần biến đổi. Trong đó:
-
kitten → sitten (thay “k” bằng “s”)
-
sitten → sittin (thay “e” bằng “i”)
-
sittin → sitting (thêm ký tự “g”) Để hiểu rõ về thuật toán, chúng ta lấy ví dụ, khoảng cách cần tính giữa hai từ source: “yu” và target: “you”. Chi phí thực hiện cho các phép biến đổi bao gồm: xoá một ký tự, thêm một ký tự và thay thế ký tự này thành ký tự khác đều là 1 (Nếu 2 ký tự giống nhau thì chi phí thực hiện là 0). Các bước thực hiện như sau:
-
Bước 1: Xây dựng ma trận lưu trữ có số hàng là M và số cột là N.
- Trong đó:
- M là số lượng các ký tự trong từ source + 1
- N là số lượng các ký tự trong từ target + 1
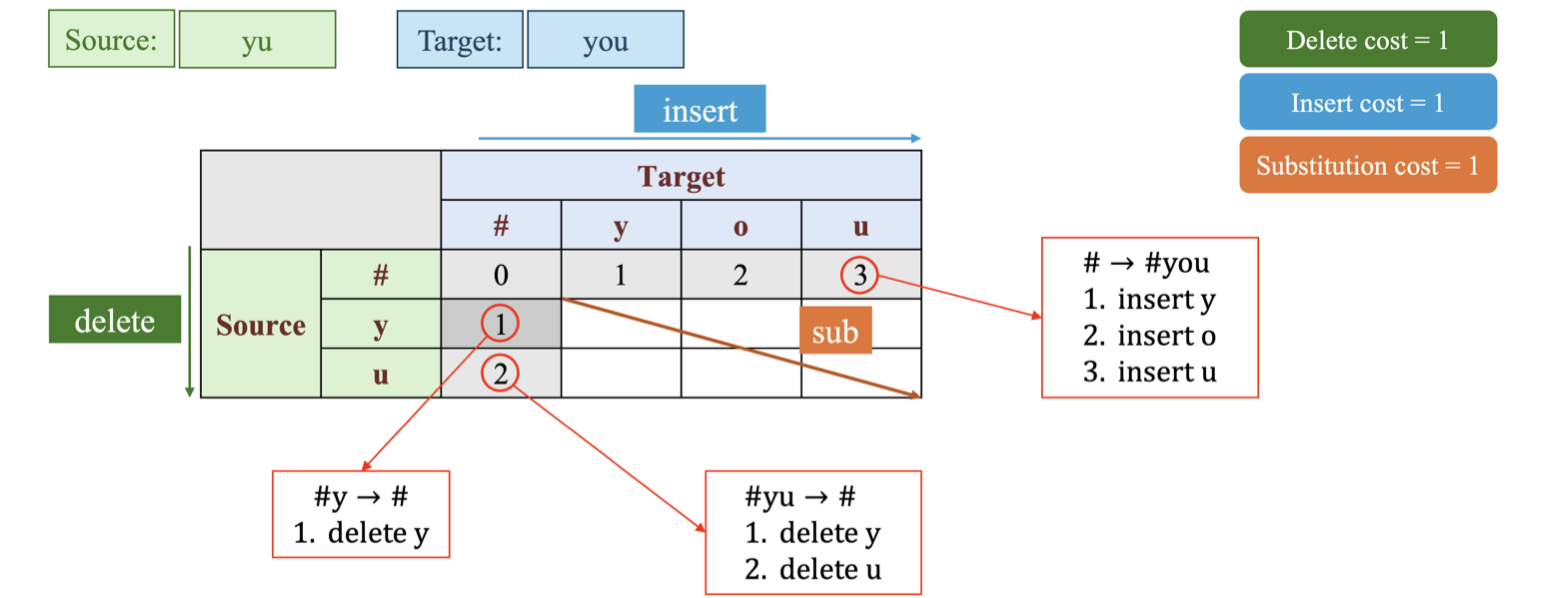
- Với ví dụ “yu” và “you”, ta có ma trận được biểu diễn như hình 1. Ký hiệu “#” đại diện cho chuỗi rỗng. Gọi là ma trận D.
- Trong đó:
-
Bước 2: Hoàn thiện hàng và cột đầu tiên.
- Với hàng đầu tiên, các giá trị đại diện cho chuỗi bắt đầu là chuỗi “#” và phép biến đổi là thêm (insert) từ chuỗi “#” thành “#”, “#y”,“#yo”, “#you” lần lượt là 0, 1, 2, 3 tương ứng với ô D[0, 0], D[0, 1], D[0, 2], D[0, 3].
- Với cột đầu tiên, các giá trị đại diện cho chuỗi “#”, “#y”, “#yu” và phép biến đổi là xoá (delete) để thu được chuỗi “#” lần lượt là: 0, 1, 2 tương ứng với ô D[0, 0], D[1, 0], D[2, 0].
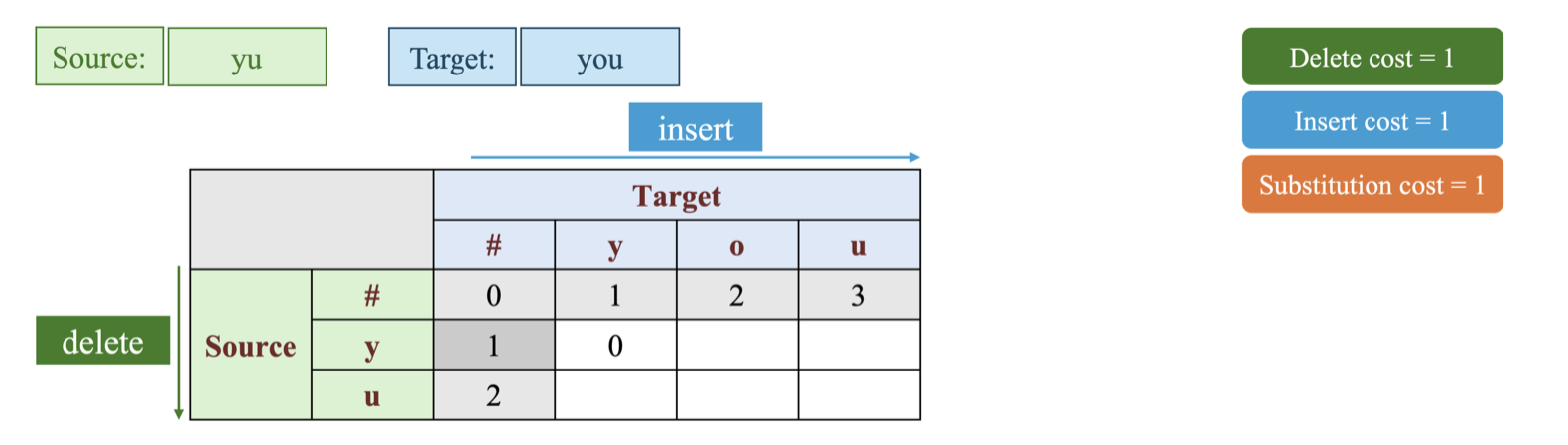
-
Bước 3. Tính toán các giá trị với các ô còn lại trong ma trận.
-
Bắt đầu từ D[1, 1] được tính dựa vào 3 ô phía trước là D[0, 1], D[1, 0], D[0, 0] như sau:
Chi phí:
del = 1,ins = 1,sub(x,y) = 0nếux=y(khớp), ngược lại1.Các giá trị biên từ hình:
D[0,1]=1,D[1,0]=1,D[0,0]=0.Vì
source[1]='y'vàtarget[1]='y'nênsub_cost('y','y')=0.→ Giữ nguyên
Vì vậy D[1, 1] = 0 ta được ma trận D như sau:
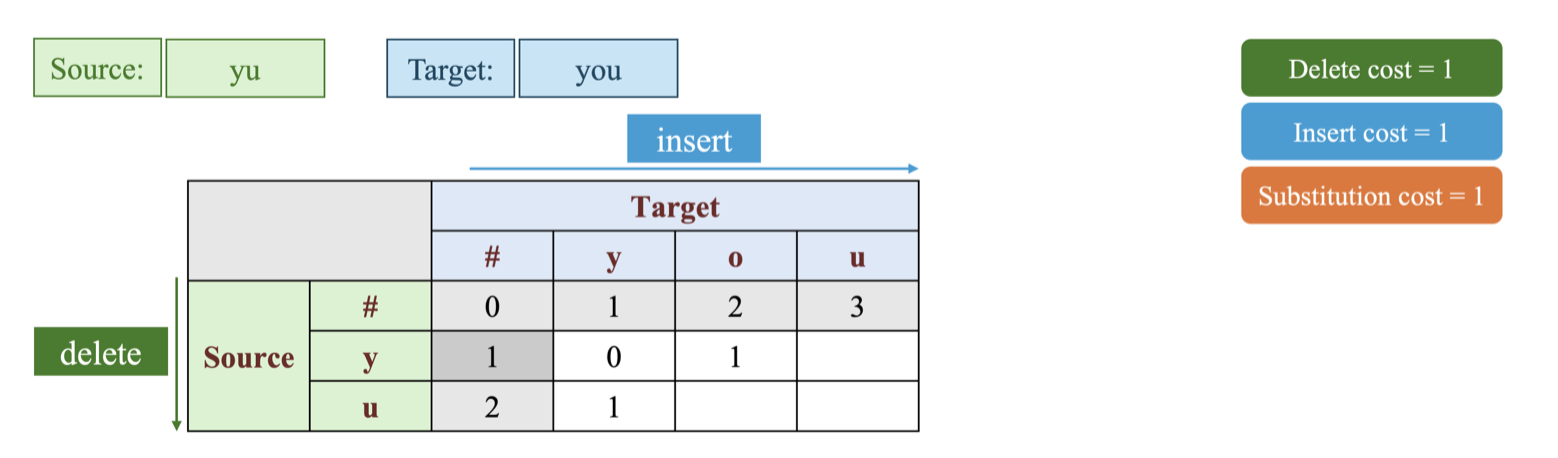
-
Tiếp theo tính D[2, 1], D[1, 2]:
→ Chèn
→ Xóa
Vì vậy D[2, 1] = 1, D[1, 2] = 1 ta được ma trận D như sau:
-
Cuối cùng, chúng ta tính D[1, 3], D[2, 2], D[2, 3]:
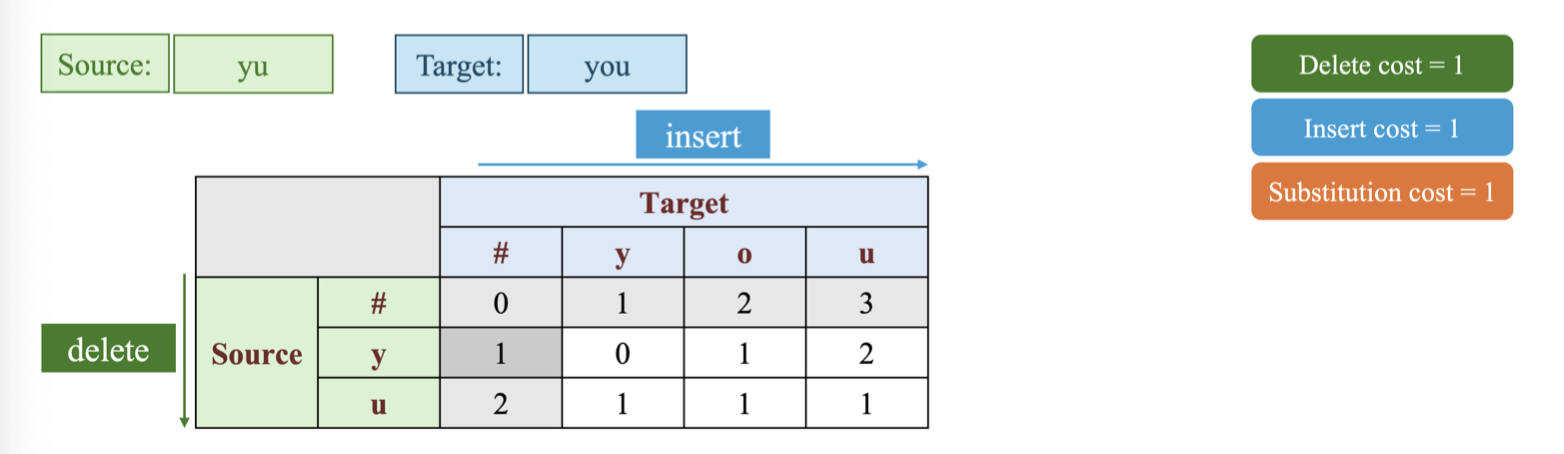
-
-
Bước 4: Sau khi hoàn thành ma trận, chúng ta đi tìm đường đi từ ô cuối cùng D[2, 3] có giá trị là 1. Vì vậy khoảng cách chỉnh sửa từ source: “yu” sang thành target: “you” là 1.
-
Cách để xác định đường đi là đánh dấu lại phép toán chúng ta lựa chọn để lấy giá trị min cho mỗi ô
- Đầu tiên ký tự “y” giữ nguyên sau đó thực hiện 1 phép thêm ký tự “o” vào sau ký tự “y” và cuối cùng ký tự “u” được giữ nguyên.
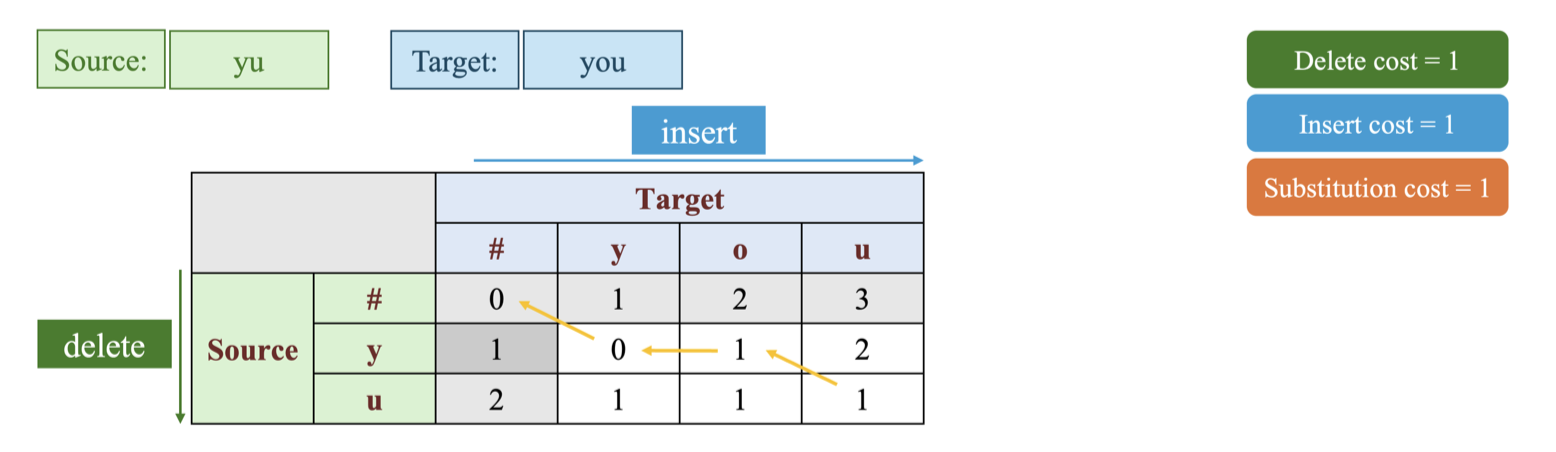
Bắt đầu từ ô cuối
Ví dụ:
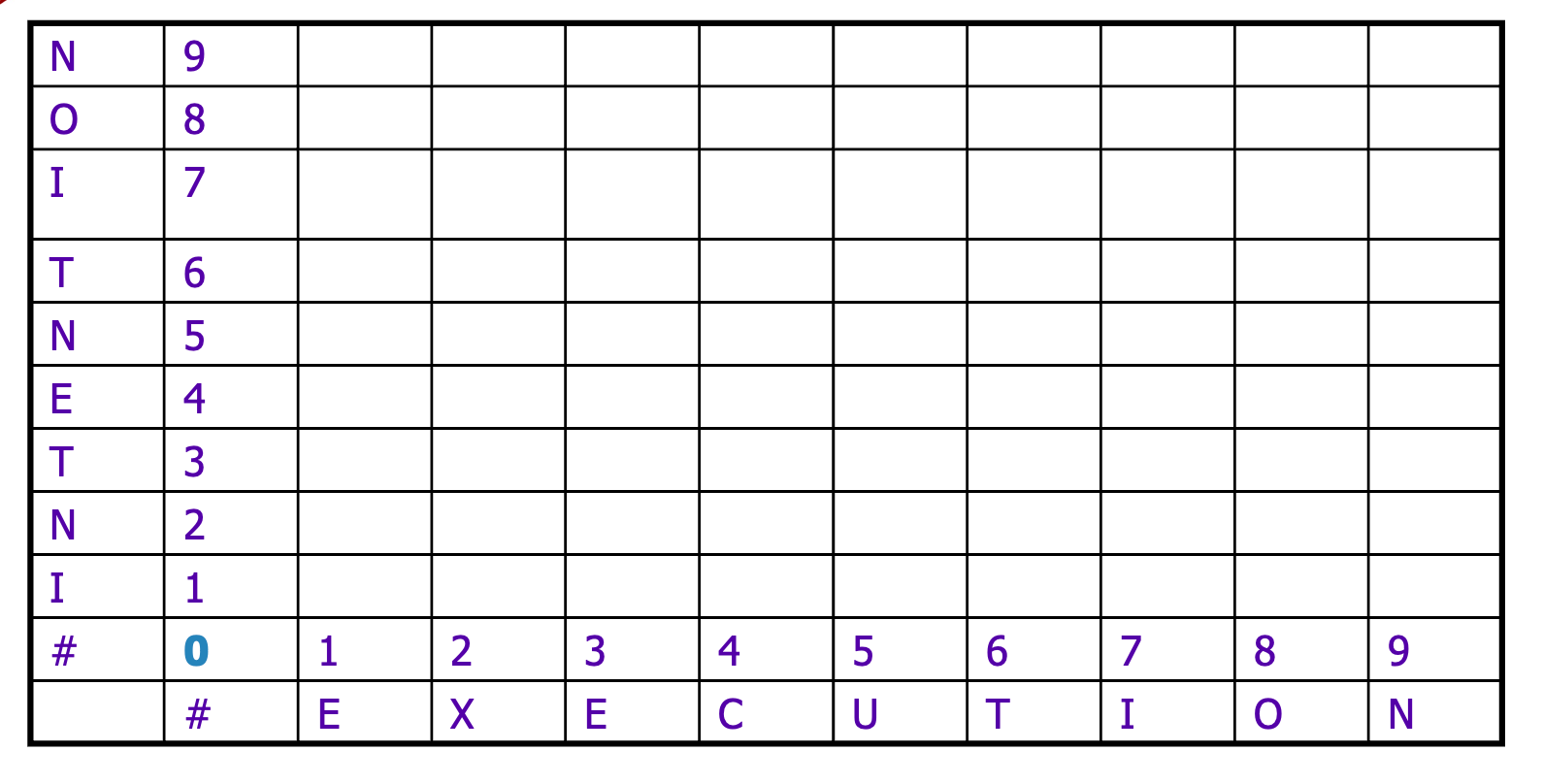 Để xác định con đường ngắn nhất, ta đánh dấu lại
Để xác định con đường ngắn nhất, ta đánh dấu lại