M01W3.6_OOP+Data Structure (Queue, Stack and Tree)

• 1. Stack Data Structure Using List
• 2. Queue
  • Queue Implementation
• 3. Tree Structure
  • What is a Tree
  • Tree Implementation
  • Tree Applications
  • Types of trees
• 4. Algorithms on Trees
  • Traversal of Binary Tree
    • Depth First Search
    • Breath First Search
  • Binary Tree
    • Balanced binary tree
    • Operations On Binary Tree
  • Binary Search Tree Review lại bài List: M01W2.4_Delving in to List

1. Stack Data Structure Using List

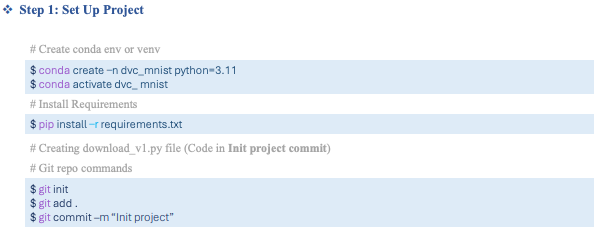Quy tắc của Stack LIFO: Last in first out (Người cuối cùng vào sẽ là người đầu tiên ra) Phần tử được thêm vào và đi ra chỉ từ một đường duy nhất Bài tập: Viết Class MyStack

• Code:

  class MyStack:
  		def __init__(self, capacity):
  				self.__capacity = capacity
  				self.__stack = []
  			
  		def push(self, value):
  				self.__stack.append(value)
  				
  		def print(self):
  		vvv

2. Queue

Queue Implementation

Using List: Using deque

from collections import deque

Using Queue

from queue import Quetue

Using List (OOP) Using dequeue (OOP)

3. Tree Structure

Motivation: Người ta thiết kế ra cấu trúc cây để giải quyết bài toán duyệt phần tử nhanh hơn. Mà bài toán duyệt phần tử được sử dụng rất nhiều → giúp cho các thao tác như tìm kiếm, chèn, xóa trở nên nhanh và hiệu quả hơn.

What is a Tree

A non-linear data structure where nodes are organized in a hierarchy 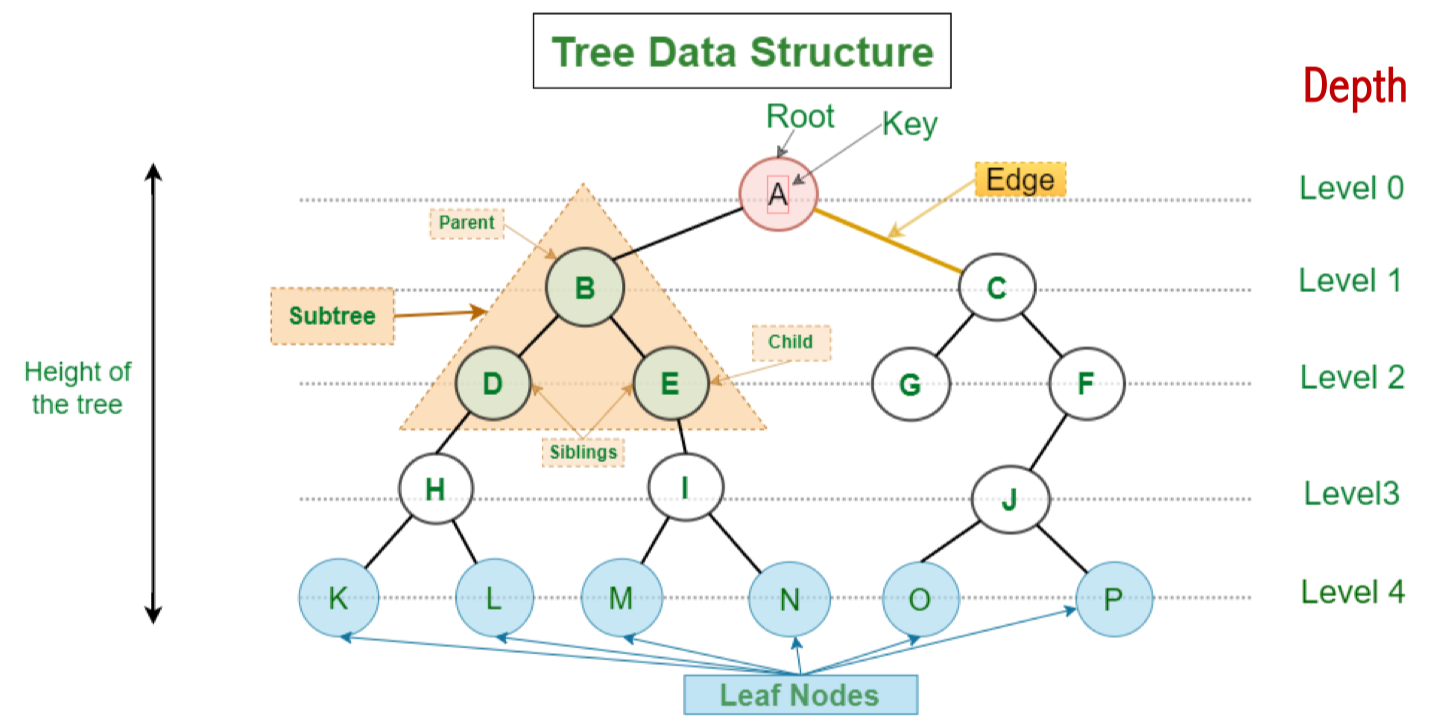Các Term:

Term	Giải thích đơn giản	Ví dụ trong cây
Parent Node (Nút cha)	Là nút đứng trên, có nhánh nối đến con	B là cha của D, E
Child Node (Nút con)	Là nút được nối ra từ cha	D, E là con của B
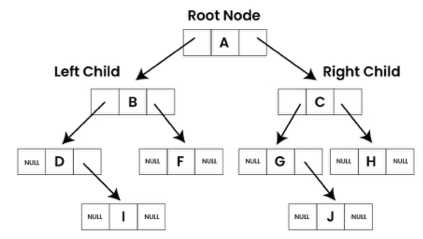
Root Node (Gốc)	Là nút cao nhất, không có cha	A là gốc cây
Leaf Node (Lá)	Là nút không có con nào	K, L, M, N, O, P, G
Ancestor (Tổ tiên)	Là tất cả các nút nằm phía trên một nút nào đó	A và B là tổ tiên của E
Sibling (Anh em)	Là các nút có cùng cha	D và E là anh em vì đều là con của B
Level / Depth (Mức/Độ sâu)	Là số bước đi từ gốc tới nút đó	A: level 0, B: level 1, E: level 2
Subtree (Cây con)	Là 1 phần cây bắt đầu từ 1 nút nào đó + các con cháu của nó	Cây con từ B gồm: B, D, E…
Height (Chiều cao)	Là số bước dài nhất từ một nút xuống tới lá	Nếu từ B đến lá xa nhất là 2 bước → height = 2

Tree Implementation

Tạo class kiểu dữ liệu TreeNode Lưu ý: Đây không phải cấu trúc Binary Tree nên ta sẽ thiết kế hơi khác.

class TreeNode:
		def __init__(self, data):
				self.data = data
				self.children = []
				self.parent = None

Các method trên Tree:

• Thêm node: Tận dụng lại Build-in function của List

class TreeNode:
		...
		def add_child(self, child):
				child.parent = self
				self.children.append(child)

• Lấy level của node

class TreeNode:
		...
		def get_level(self): \#to get level of each node
				level = 0
				p = self.parent
				while p:
						level += 1
						p = p.parent
				return level

• Vẽ tree:

class TreeNode:
		...
		def print_tree(self):
		space = ' ' * self.get_level() * 3
		prefix = space + '|__' if self-parent else ''
		print (prefix + self.data) \#add prefix
		if self.children:
				for child in self.children:
						child.print_tree()
		

• Create tree:

def create_tree():
		a_node = TreeNode ("A" )
		b_node = TreeNode ("B" )
		c_node = TreeNode ("(" )
		d_node = TreeNode ("D" )
		e_node = TreeNode ("E")
		f_node = TreeNode ("F")
		g_node = TreeNode("G" )
		
		a_node.add_child(b_node)
		a_node.add_child(c_node)
		
		b_node.add_child(d_node)
		b_node.add_child(e_node)
		
		c_node.add_child(f_node)
		c_node.add_child(g_node)
		return a_node

tree = create_tree()
tree.print_tree()
 
>>A
	|__B
		 |__D
		 |__E
	|__C
		 |__F
		 |__G

Tree Applications

Types of trees

4. Algorithms on Trees

Traversal of Binary Tree

Depth First Search

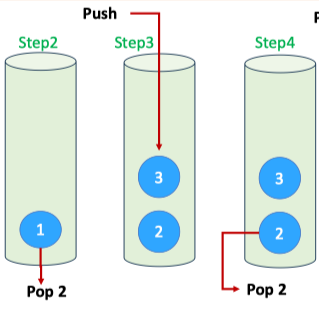
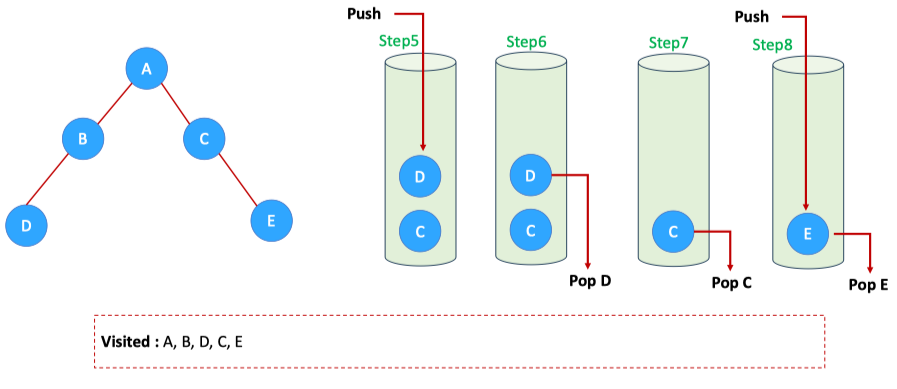Using Stack

def dfs(sefl):

Debug:

Breath First Search

Dùng cấu trúc dữ liệu queue

def bfs(self):
		

Chạy tay:

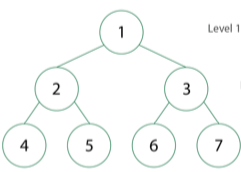
Binary Tree

• Một cây nhị phân là một cấu trúc mà mỗi nút chỉ có nhiều nhất hai nhánh con.
• Mỗi nhánh chia ra như một cái cây thật ngoài đời.
• Mỗi nhánh con có thể tiếp tục chia tiếp — giống như cây có nhiều nhánh con nhỏ.

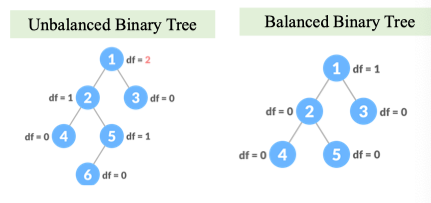
Chiều cao = độ dài của nhánh dài nhất. Độ cao của Tree 1 node = 0

Balanced binary tree

Chiều cao = độ dài của nhánh dài nhất. Độ cao của Tree 1 node = 0 Điều kiện Balance tree:

• Độ dài của các nhánh không lớn hơn 1
• Left subtree is balanced
• Right subtree is balanced Tại sao phải cân bằng cây? 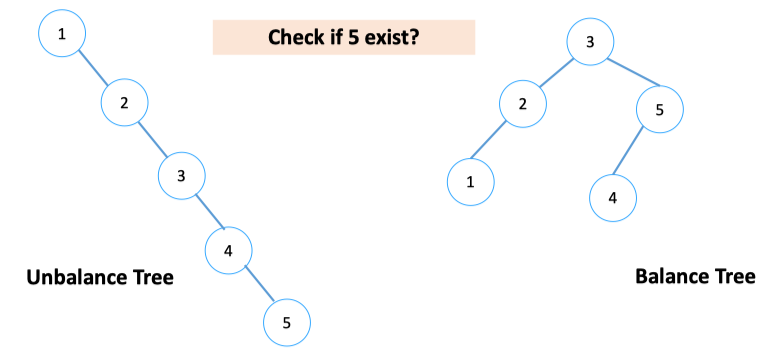→ Khi cây mất cân bằng, việc duyệt cây chả khác gì duyệt trên List ⇒ không tối ưu thời gian và thuật toán tìm kiếm.

Operations On Binary Tree

Insert a Node:

def insert_node(root, key):

Cách insert cho cây cân bằng:

→ Sẽ tốn thời gian lúc đầu nhưng về sau cây sẽ cân bằng và tiết kiệm thời gian search. Ý tưởng để đảm bảo cây cân bằng: chèn → kiểm tra cân bằng → ko cân bằng → xoay cho cân bằng. Xoay như nào?

Delete a Node: Trường hợp xóa root:

Tree visualization Dùng thư viện from graphviz import Graph để vẽ graph:

def draw_tree(root):
		

Limitations: Although suitable for storing hierarchical data, binary trees of this general form don’t guarantee a fast lookup. Let’s take as the example the search for number 9 in the above tree. 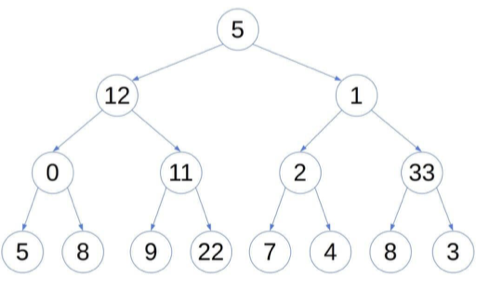Whichever node we visit, we don’t know if we should traverse the left or the right sub-tree next. That’s because the tree hierarchy doesn’t follow the relation

Binary Search Tree

• Nhánh trái phải lớn hơn nhánh phải Binary Search Tree Implementation:

class BST:
		

Search Algorithm in BST: