I. Mở đầu
II. Cấu trúc dữ liệu nền tảng: Stack và Queue
- 1. Stack – Ngăn xếp
- 2. Queue - Hàng đợi
III. Tree – Cây nhị phân và cấu trúc cây tổng quát
IV. Binary Tree – Cây nhị phân
V. Binary Search Tree (BST) – Cây tìm kiếm nhị phân
VI. Ứng dụng của cây
VII. Thực hành & Bài tập
- Bài tập thực hành
- Bài tập ứng dụng
VIII. Mở rộng – Các phép cân bằng BST
- 1. Vì sao cần cân bằng BST?
- 2. Cây tự cân bằng là gì?
  - Cây AVL (Adelson-Velsky and Landis)
  - Cây Đỏ Đen (Red-Black Tree)
  - Cây B-Trees (cho hệ thống lưu trữ)
  - Tóm tắt các phương pháp cân bằng:
  - Câu hỏi mở rộng: Bài viết này có tham khảo từ Slide bài giảng về Data Structure Tree của AIO và có prompt Chat GPT

I. Mở đầu

Trong thế giới lập trình, khi dữ liệu trở nên lớn hơn và phức tạp hơn, chúng ta không chỉ cần biết lưu trữ thông tin, mà còn cần tổ chức thông tin sao cho dễ truy xuất và xử lý nhanh. Đó chính là lý do vì sao cấu trúc dữ liệu (data structure) ra đời. Ở cấp độ cơ bản, bạn có thể đã quen với mảng (array) hay danh sách liên kết (linked list). Chúng đơn giản, dễ dùng — nhưng chỉ thích hợp cho những bài toán tuyến tính, nơi dữ liệu nằm theo một hàng ngang: trước → sau. Nhưng… nếu bạn cần mô phỏng cấu trúc thư mục trên máy tính, tổ chức phả hệ gia đình, hoặc duyệt các lựa chọn trong một trò chơi hay thuật toán AI? Ví dụ ứng dụng: Khi bạn chơi cờ vua, hay chơi một trò chơi giải đố, bạn thường phải nghĩ:

“Nếu mình đi nước này, thì đối phương sẽ làm gì? Sau đó mình sẽ đáp lại ra sao?” Vậy là bạn xét từng lựa chọn, và từng kết quả sau mỗi lựa chọn. Giả sử bạn có 3 nước đi ban đầu → mỗi nước đi lại tạo ra 2-3 tình huống khác → rồi mỗi tình huống lại chia ra nữa… 📌 Cấu trúc này giống hệt như một cái cây, nơi mỗi “nhánh” đại diện cho một khả năng. 👉 Khi đó, các cấu trúc tuyến tính là không đủ. Đây chính là lúc cây (tree) xuất hiện. Cây là một cấu trúc dữ liệu phi tuyến (non-linear), cho phép bạn biểu diễn mối quan hệ phân cấp giữa các phần tử. Mỗi phần tử (gọi là node) có thể dẫn đến nhiều phần tử khác — giống như một câu hỏi có nhiều đáp án, hoặc một thư mục chứa nhiều tệp con. Trong loạt bài blog này, chúng ta sẽ cùng nhau khám phá:

Cây là gì và vì sao nó quan trọng?
Các loại cây cơ bản như cây nhị phân, cây tìm kiếm nhị phân (BST)
Cách duyệt cây, thao tác với cây
Ứng dụng của cây trong thực tế như file explorer, HTML DOM, thuật toán AI… Và để hiểu cách cây hoạt động, trước tiên ta sẽ bắt đầu với Stack và Queue – hai cấu trúc dữ liệu cơ bản giúp bạn duyệt cây một cách hiệu quả.

II. Cấu trúc dữ liệu nền tảng: Stack và Queue

Trước khi tìm hiểu cách hoạt động của cây, bạn cần nắm vững hai công cụ cực kỳ quan trọng giúp duyệt cây: Stack (ngăn xếp) và Queue (hàng đợi).

1. Stack – Ngăn xếp

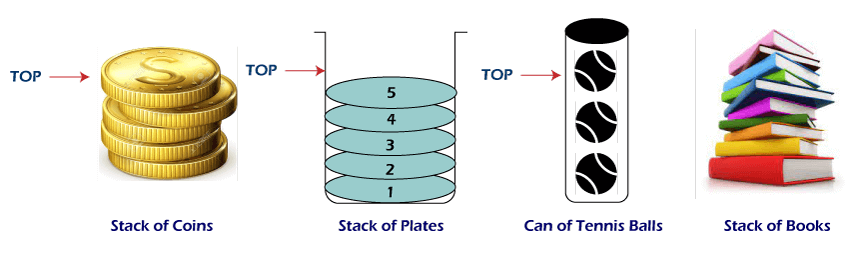
Stack là một cấu trúc dữ liệu tuân theo nguyên tắc LIFO – Last In, First Out: Vật được đặt lên trên cùng sẽ phải được tháo/lấy ra trước. 🧠 Hình dung đơn giản: Bạn xếp sách chồng lên nhau. Cuốn bạn đặt cuối cùng ở trên cùng — và khi lấy ra, bạn sẽ phải lấy cuốn trên cùng trước. image 1 48.png ⚙️ Các thao tác cơ bản:

push(x): đưa x vào đỉnh ngăn xếp
pop(): lấy phần tử trên cùng ra ngoài
peek(): xem phần tử trên cùng mà không lấy ra
is_empty(): kiểm tra stack rỗng không Cài đặt Stack trong Python:

2. Queue - Hàng đợi

Queue tuân theo nguyên tắc FIFO – First In, First Out: cái nào vào trước thì được lấy ra trước. 🧠 Hình dung đơn giản: Bạn xếp hàng chờ mua trà sữa. Ai đến trước được phục vụ trước. image 2 46.png ⚙️ Các thao tác cơ bản:

enqueue(x): thêm x vào cuối hàng
dequeue(): lấy phần tử đầu tiên ra
peek(): xem phần tử đầu mà không lấy ra
is_empty(): kiểm tra hàng có rỗng không Cài đặt Queue trong Python:

III. Tree – Cây nhị phân và cấu trúc cây tổng quát

1. Cây là gì:

Cây là một cấu trúc dữ liệu phi tuyến (non-linear), nơi các phần tử gọi là node được tổ chức theo kiểu phân cấp (hierarchical). Mỗi node có thể có nhiều node con, nhưng chỉ có một node gốc (root) và không có vòng lặp. 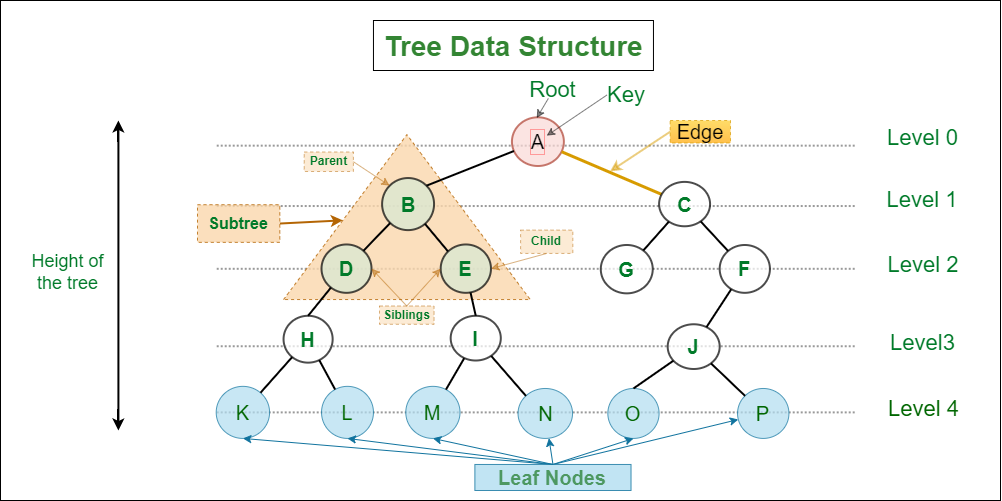image 3 43.png Một số thuật ngữ quan trọng:


Thuật ngữ	Giải thích
Root (Gốc)	Node đầu tiên, không có cha
Parent (Cha)	Node có nhánh dẫn đến node khác
Child (Con)	Node được nối từ node cha
Leaf (Lá)	Node không có con
Sibling (Anh/Em)	Các node có cùng cha
Ancestor (Tổ tiên)	Node nằm trên đường đi từ gốc đến node nào đó
Level	Số bậc từ gốc đến node (root là level 0)
Depth	Chiều sâu của một node so với root
Height	Chiều cao của node: số bước dài nhất đến lá
Subtree	Một node cùng tất cả con cháu của nó
Ví dụ:

Root: A
Child of A → B, C
Child of B → D, E
D ,E là Leaf (lá)
Ancestor của E (tổ tiên :v nghe chuối ghê) → A, B
B và C là Sibling (anh em)

2. Cài đặt Tree:

Cấu trúc node cơ bản: Tạo cấu trúc dữ liệu node cho Tree

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

Với cây nhị phân, mỗi node có tối đa 2 con: left và right. Dựng cây bằng tay: Hãy thử dựng một cây với cấu trúc sau:

     A
    / \
   B   C
  / \
 D   E

Code:

root = Node("A")
root.left = Node("B")
root.right = Node("C")
root.left.left = Node("D")
root.left.right = Node("E")

Theo hướng OOP: Tạo class BinaryTree, đóng gói logic thêm/xoá/tìm kiếm node, hoặc ghi nhớ root:

class BinaryTree:
    def __init__(self, root_value):
        self.root = Node(root_value)

Điều này giúp tách dữ liệu (node) khỏi hành vi (thao tác trên cây), tuân theo nguyên tắc lập trình hướng đối tượng.

3. Duyệt cây – Traversal

Duyệt cây nghĩa là đi qua từng node trong cây một cách có hệ thống → để in ra, xử lý hoặc tìm kiếm.

DFS - Depth First Search (Duyệt theo chiều sâu)

Sử dụng Stack (hoặc đệ quy). Ba kiểu phổ biến:

Preorder: gốc → trái → phải
Inorder: trái → gốc → phải
Postorder: trái → phải → gốc

BFS - Breadth First Search (Duyệt theo chiều rộng)

Sử dụng Queue để duyệt theo từng level của cây.

from collections import deque
def bfs(root):
    queue = deque([root])
    while queue:
        node = queue.popleft()
        print(node.value)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

So sánh hiệu năng và nhận xét

[Todo]

IV. Binary Tree – Cây nhị phân

1. Định nghĩa và phân loại

Cây nhị phân là gì?

Cây nhị phân (Binary Tree) là cây mà mỗi node chỉ có tối đa 2 con, thường được gọi là

left (bên trái)
right (bên phải)

Việc giới hạn này giúp cây dễ triển khai, thao tác và ứng dụng trong các thuật toán.

Các loại cây nhị phân


Loại cây	Đặc điểm
Full Binary Tree	Mỗi node hoặc có 0 hoặc 2 con
Perfect Binary Tree	Mọi node đều đầy đủ 2 con, và tất cả các lá ở cùng mức
Complete Binary Tree	Tất cả các mức đều đầy trừ mức cuối cùng, và các node được điền từ trái sang phải
Skewed Tree (Lệch trái/phải)	Mỗi node chỉ có 1 con: lệch hết về trái hoặc phải (giống linked list)
Balanced Binary Tree	Độ cao giữa trái và phải của bất kỳ node nào chênh lệch không quá 1
Unbalanced Tree	Một nhánh dài vượt trội khiến cây nghiêng hẳn về một phía, làm giảm hiệu năng tìm kiếm

Perfect Binary Tree:
        A
       / \
      B   C
     / \ / \
    D  E F  G
Skewed Left Tree:
    A
   /
  B
 /
C
Unbalanced Tree:
        A
       / \
      B   C
     / \ 
    D  E

2. Các thao tác cơ bản

Thêm node (Insert)

Để thêm một node mới vào cây nhị phân không theo thứ tự, ta thường dùng Level-Order Traversal (BFS) để tìm node đầu tiên còn thiếu con. Ý tưởng:

Bắt đầu từ gốc
Dùng Queue duyệt lần lượt từng node
Nếu node nào thiếu con trái → thêm vào trái
Nếu không → kiểm tra phải

Xoá node (Delete)

Ý tưởng:

Tìm node cần xoá
Thay nó bằng node sâu nhất (deepest rightmost)
Xoá node sâu nhất khỏi cây Lý do: Giữ nguyên cấu trúc và thứ tự duyệt level-order của cây.

3. Hạn chế của Binary Tree thông thường:

Không đảm bảo cấu trúc cân bằng → hiệu năng tìm kiếm có thể giảm từ O(log n) xuống O(n)
Không có quy tắc sắp xếp → không áp dụng tốt cho bài toán tìm kiếm như BST 👉 Chính vì thế, Binary Search Tree (BST) – phiên bản sắp xếp của Binary Tree – ra đời để khắc phục các hạn chế trên. Đó sẽ là nội dung ở phần tiếp theo.

V. Binary Search Tree (BST) – Cây tìm kiếm nhị phân

Sau khi học về cây nhị phân thường, bạn sẽ thấy có một điểm yếu: không có quy luật sắp xếp nào giữa các node. Vì vậy, muốn tìm kiếm một giá trị, bạn vẫn phải duyệt lần lượt toàn bộ cây – rất tốn thời gian. Giải pháp là: Cây tìm kiếm nhị phân (Binary Search Tree – BST).

1. Định nghĩa: BST là gì?

BST là một loại cây nhị phân có thêm quy tắc sắp xếp rất quan trọng:

Với mỗi node x:

Tất cả node trong cây con trái có giá trị nhỏ hơn x

Tất cả node trong cây con phải có giá trị lớn hơn hoặc bằng x 💡 Chính quy tắc này giúp tìm kiếm nhanh hơn rất nhiều. 📈 Ưu điểm:

Tìm kiếm nhanh: thời gian trung bình O(log n) nếu cây cân bằng
Thêm và xóa có thể giữ nguyên tính chất sắp xếp
Áp dụng trong nhiều thuật toán: sắp xếp, từ điển, auto-complete, v.v.

2. Cài đặt và thuật toán

Tìm kiếm node (Search)

def search(node, key):
    if not node:
        return False
    if node.value == key:
        return True
    elif key < node.value:
        return search(node.left, key)
    else:
        return search(node.right, key)

BST giống như chơi trò “chia đôi tìm kiếm” – bạn liên tục so sánh với node hiện tại và rẽ trái/phải tùy vào giá trị. B. Thêm node (Insert) Khi thêm một node mới:

So sánh với node hiện tại
Nếu nhỏ hơn → chèn vào cây con trái
Nếu lớn hơn hoặc bằng → chèn vào cây con phải

def insert(node, key):
    if not node:
        return Node(key)
    if key < node.value:
        node.left = insert(node.left, key)
    else:
        node.right = insert(node.right, key)
    return node

C. Xoá node (Delete) Có 3 trường hợp khi xoá:

Node là lá → xóa luôn
Node có 1 con → nối con đó với cha
Node có 2 con → thay bằng node nhỏ nhất bên phải (hoặc lớn nhất bên trái)

def delete(node, key):
    if not node:
        return None
    if key < node.value:
        node.left = delete(node.left, key)
    elif key > node.value:
        node.right = delete(node.right, key)
    else:
        # Node có 1 hoặc 0 con
        if not node.left:
            return node.right
        if not node.right:
            return node.left
        # Node có 2 con: tìm node kế tiếp nhỏ nhất
        min_larger = find_min(node.right)
        node.value = min_larger.value
        node.right = delete(node.right, min_larger.value)
    return node
def find_min(node):
    while node.left:
        node = node.left
    return node

3. So sánh với Binary Tree thường


Tiêu chí	Binary Tree thường	Binary Search Tree (BST)
Quy tắc trái/phải	Không có	Có: trái < node < phải
Tìm kiếm	Phải duyệt toàn bộ	Duyệt theo hướng rẽ nhánh
Thêm	Đơn giản, không cần so sánh	Phải đúng vị trí để giữ sắp xếp
Xoá	Dễ hơn nhưng không tối ưu	Phức tạp hơn nhưng hiệu quả
📌 Lưu ý:
BST hoạt động tốt nhất khi cân bằng. Nếu thêm theo thứ tự tăng dần (`1 → 2 → 3 → 4`), cây sẽ lệch hẳn sang phải, và bạn lại quay về hiệu suất `O(n)` như danh sách liên kết.
Vì vậy, người ta dùng thêm các phiên bản nâng cấp như:

AVL Tree
Red-Black Tree

VI. Ứng dụng của cây

Sau khi đã học cách cây hoạt động và cách thao tác với nó, câu hỏi quan trọng là:

“Cây được dùng để làm gì trong thực tế?” Câu trả lời là: Rất nhiều thứ quen thuộc bạn đang dùng mỗi ngày hoạt động dựa trên cấu trúc cây.

1. Hệ thống tệp (File Explorer)

Khi bạn mở File Explorer (Windows) hay Finder (macOS), bạn sẽ thấy:

Một thư mục gốc (ổ C:, ổ D:)
Trong đó có các thư mục con
Mỗi thư mục lại chứa thêm thư mục hoặc tệp 📌 Đây chính là một cây phân cấp:
Gốc: ổ đĩa
Node cha: thư mục
Node con: thư mục con hoặc tệp
Lá: là các tệp không chứa gì bên trong

2. HTML DOM

Khi bạn mở một trang web, trình duyệt phân tích file HTML thành một cây DOM (Document Object Model). Ví dụ:

<html>
  <body>
    <h1>Xin chào</h1>
    <p>Đây là đoạn văn</p>
  </body>
</html>

Cây DOM tương ứng:

     html
      |
    body
   /    \
 h1      p

📌 Mỗi thẻ HTML là một node. Cây DOM giúp:

Trình duyệt hiển thị cấu trúc web
Lập trình viên thao tác với từng phần tử bằng JavaScript (ví dụ: document.querySelector('p'))

3. Decision Tree (Machine Learning)

Trong Machine Learning, Decision Tree là mô hình học đơn giản và dễ hiểu:

Mỗi node là một câu hỏi (ví dụ: “Tuổi > 18?”)
Mỗi nhánh là câu trả lời (Có/Không)
Lá là kết luận (ví dụ: “Phê duyệt vay tiền”)

    Tuổi > 18?
      /      \
    Không    Có
   Từ chối  Thu nhập > 10tr?
              /      \
          Không     Duyệt
         Từ chối

📌 Đây là cách mà AI tự học việc ra quyết định dựa trên dữ liệu.

4. K-D Tree – Tìm kiếm không gian (AI/Graphics)

K-D Tree (K-Dimensional Tree) dùng để tìm kiếm điểm gần nhất trong không gian nhiều chiều. Ứng dụng:

Tìm địa điểm gần bạn nhất (Google Maps)
Nhận diện ảnh bằng so sánh đặc trưng khuôn mặt
Phân loại nhanh điểm dữ liệu trong không gian 📌 Nó chia không gian theo từng chiều (x, y, z…) thành cây nhị phân để tìm nhanh hơn nhiều lần so với duyệt toàn bộ.

5. Các hệ thống phân cấp dữ liệu

Rất nhiều hệ thống trong đời sống dùng cây để biểu diễn:

Sơ đồ tổ chức công ty (CEO → quản lý → nhân viên)
Cây phả hệ (Ông bà → cha mẹ → con cháu)
Menu dropdown (Danh mục → phụ mục → sản phẩm) 📌 Mọi thứ có “cha – con – cháu” đều có thể biểu diễn bằng cây.

VII. Thực hành & Bài tập

Dưới đây là một số bài thực hành được thiết kế theo cấp độ tăng dần, giúp bạn chuyển từ hiểu đến thành thạo.

Bài tập thực hành

1. Tạo cây nhị phân đơn giản bằng Python

Viết class Node và dựng cây sau:

➡️ Sau đó in ra value của từng node bằng các cách duyệt: preorder, inorder, postorder.

2. Cài đặt thuật toán duyệt cây

Viết hàm preorder(node) (DFS)
Viết hàm bfs(root) (BFS dùng deque) 💡 Gợi ý:
DFS có thể dùng đệ quy hoặc stack
BFS dùng hàng đợi (collections.deque)

3. Thêm node vào cây nhị phân thường

Viết hàm insert(root, value):

Duyệt theo level-order (BFS)
Tìm node đầu tiên chưa có con trái/phải để chèn vào

Bài tập ứng dụng

4. Xây dựng BST và tìm kiếm

Tạo một BST với dữ liệu: [8, 3, 10, 1, 6, 14, 4, 7, 13]

Viết hàm tìm kiếm search(root, key)
Kiểm tra: giá trị 6 có tồn tại không?

5. Xóa node trong BST

Viết hàm delete(root, key) để:

Xóa node lá
Xóa node có 1 con
Xóa node có 2 con (thay bằng node nhỏ nhất cây con phải) ✅ Kiểm tra bằng ví dụ: xóa lần lượt các node 1, 6, 3 trong BST ở bài 4.

6. Vẽ cây DOM HTML đơn giản bằng sơ đồ

Cho đoạn HTML:

<body>
  <div>
    <h1>Title</h1>
    <p>Paragraph</p>
  </div>
</body>

Hãy vẽ sơ đồ cây thể hiện DOM tương ứng.

7. Mô phỏng cây quyết định đơn giản

Bạn hãy mô phỏng cây quyết định sau: Viết hàm Python để hỏi người dùng `input()` và in ra kết quả phù hợp.

📌 Cách học hiệu quả:

Viết tay trước khi chạy code
Thử sai – sửa lỗi – debug
Vẽ cây bằng tay để hình dung rõ ràng
Nếu hiểu rõ, hãy thử viết lại bằng OOP (dùng class BinaryTree)

VIII. Mở rộng – Các phép cân bằng BST

1. Vì sao cần cân bằng BST?

Cây tìm kiếm nhị phân (BST) chỉ thật sự hiệu quả nếu nó cân bằng. Nếu bạn thêm các phần tử theo thứ tự tăng dần như [1, 2, 3, 4, 5], BST sẽ trở thành một cây lệch phải giống như danh sách liên kết:

➡️ Khi đó, các thao tác tìm kiếm, chèn, xoá đều có độ phức tạp O(n) thay vì O(log n). 💡 Giải pháp: Áp dụng các kỹ thuật cân bằng cây để giữ BST luôn gọn gàng và hiệu quả.

2. Cây tự cân bằng là gì?

Là cây BST tự động điều chỉnh lại cấu trúc sau mỗi thao tác thêm/xoá để giữ cho cây luôn gần như cân bằng. Dưới đây là các kỹ thuật phổ biến:

Cây AVL (Adelson-Velsky and Landis)

Đặc điểm:

Với mọi node, độ chênh lệch chiều cao giữa cây con trái và phải ≤ 1
Nếu chênh lệch xảy ra → thực hiện xoay (rotation) để cân bằng lại Các loại xoay:
Xoay đơn trái (Right Rotation): khi cây lệch trái
Xoay đơn phải (Left Rotation): khi cây lệch phải
Xoay kép trái-phải / phải-trái: khi cây lệch kiểu chữ Z 📌 AVL cực kỳ chặt chẽ trong việc giữ cân bằng → đảm bảo hiệu năng cao

Cây Đỏ Đen (Red-Black Tree)

= )) Đặc điểm:

Mỗi node có màu đỏ hoặc đen
Đảm bảo không có hai node đỏ liên tiếp
Đường đi từ gốc đến mỗi lá có số lượng node đen bằng nhau ➡️ Luật màu được dùng để xác định khi nào cần xoay hoặc đổi màu node 📌 Dù không luôn hoàn hảo cân bằng, cây đỏ đen đảm bảo chiều cao tối đa chỉ là 2*log(n) Ứng dụng:
Là cấu trúc của TreeMap, TreeSet trong Java
Dùng trong Linux kernel, các hệ thống database

Cây B-Trees (cho hệ thống lưu trữ)

Là cây tìm kiếm đa nhánh (không chỉ 2 nhánh như BST)
Thường dùng trong cơ sở dữ liệu, ổ đĩa, hệ thống file
Giảm chiều cao bằng cách tăng số phần tử mỗi node → phù hợp với lưu trữ trên đĩa

Tóm tắt các phương pháp cân bằng:


Loại cây	Cân bằng chặt	Chiều cao	Dễ cài đặt	Dùng trong
AVL	Rất chặt	log(n)	Khó hơn	Tìm kiếm yêu cầu tốc độ cao
Red-Black	Vừa phải	≤ 2log(n)	Dễ hơn AVL	Hệ thống thực tế, chuẩn thư viện
B-Tree	Linh hoạt	thấp hơn do nhiều nhánh	Phức tạp	Hệ thống lưu trữ, CSDL

Câu hỏi mở rộng:

Trong trường hợp nào bạn nên dùng AVL thay vì Red-Black Tree?
Nếu bạn đang xây dựng từ điển tìm kiếm, bạn sẽ chọn loại cây nào?
Liệu có thể cân bằng cây nhị phân thường thủ công sau khi xây xong?

An Hoai Thai's Notes

Trong bài này

Tree and Its Applications