I. Event
1.1 Experiment (Thí nghiệm)
- Định nghĩa: Là một hành động hoặc quá trình mà bạn thực hiện theo những điều kiện nhất định để quan sát kết quả.
- Ví dụ: Tung một đồng xu, gieo một viên xúc xắc, chọn ngẫu nhiên một lá bài.
1.2 Outcome (Kết quả)
- Định nghĩa: Là kết quả có thể xảy ra duy nhất của một lần thực hiện thí nghiệm.
- Ví dụ:
- Tung một đồng xu → kết quả có thể là “ngửa” hoặc “sấp” → mỗi cái là một outcome.
- Gieo một viên xúc xắc → kết quả có thể là 1, 2, 3, 4, 5, 6 → mỗi số là một outcome.
1.3 Sample space (Không gian mẫu)
- Định nghĩa: Là tập hợp tất cả các outcome có thể xảy ra của thí nghiệm.
- Ký hiệu: thường ký hiệu là S hoặc Ω.
- Ví dụ:
-
Tung một đồng xu:
→ Không gian mẫu: S = {ngửa, sấp}
-
Gieo một viên xúc xắc:
→ Không gian mẫu: S = {1, 2, 3, 4, 5, 6}
-
1.4 Event (Biến cố)
- Định nghĩa: Là một tập con của sample space, tức là một hoặc nhiều outcome cụ thể.
- Ví dụ:
-
Thí nghiệm gieo xúc xắc.
→ Event A = “ra số chẵn” = {2, 4, 6}
→ Event B = “ra số 5” = {5}
→ Event C = “ra số lớn hơn 6” = {} (event này là rỗng)
-
1.5 Certain Event (Biến cố chắc chắn)
- Định nghĩa: Là biến cố luôn xảy ra trong mỗi lần thực hiện thí nghiệm.
- Ký hiệu: Ω (toàn bộ không gian mẫu).
- Ví dụ:
- Gieo xúc xắc 1 lần → Biến cố “ra một số từ 1 đến 6” luôn đúng → đây là biến cố chắc chắn.
- Chọn 1 lá bài từ bộ bài 52 lá → Biến cố “chọn được một lá bài” luôn xảy ra.
1.6 Impossible Event (Biến cố không thể xảy ra)
- Định nghĩa: Là biến cố không bao giờ xảy ra, tức là không có outcome nào trong không gian mẫu thỏa mãn.
- Ký hiệu: ∅ (tập rỗng).
- Ví dụ:
- Gieo xúc xắc → Biến cố “ra số 7” là không thể xảy ra → là ∅.
- Tung một đồng xu → Biến cố “ra cả ngửa và sấp cùng lúc” là bất khả thi.
1.7 Random Event (Biến cố ngẫu nhiên)
- Định nghĩa: Là biến cố có thể xảy ra hoặc không xảy ra trong mỗi lần thực hiện thí nghiệm.
- Ví dụ:
- Gieo xúc xắc → Biến cố A = “ra số chẵn” = {2, 4, 6} → có thể xảy ra hoặc không.
- Chọn 1 người ngẫu nhiên → Biến cố B = “người đó cao trên 1m80” → có thể đúng hoặc sai.
1.8 Random Experiment (Thí nghiệm ngẫu nhiên)
- Định nghĩa: Là một thí nghiệm mà kết quả không xác định trước được, chỉ biết các khả năng có thể xảy ra.
- Ví dụ:
-
Tung đồng xu, gieo xúc xắc, chọn bài ngẫu nhiên, đo chiều cao của người bất kỳ,…
→ đều là các thí nghiệm ngẫu nhiên.
-
Ký hiệu biến cố
- Để tiện viết và phân tích, các biến cố thường được đặt tên bằng chữ cái in hoa như: A, B, C,…
II. Operations with Events
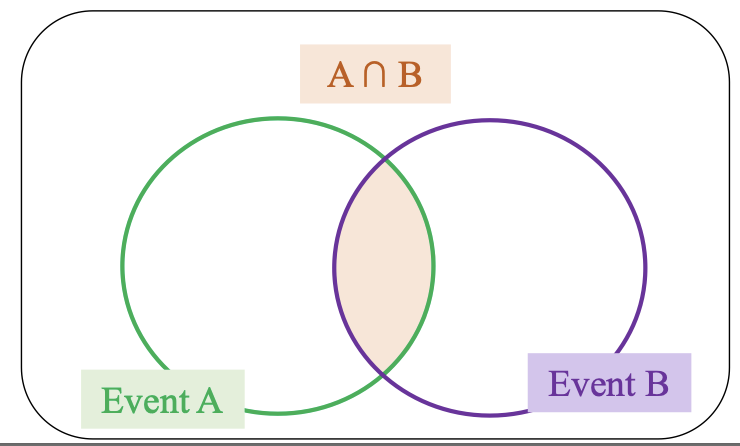
2.1 Intersection of events (giao của hai biến cố)
-
Định nghĩa:
Là tập hợp các kết quả đồng thời thuộc về sự kiện A và sự kiện B, ký hiệu là A ∩ B.
Khi đó, xác suất xảy ra đồng thời cả hai sự kiện A và B được ký hiệu là: P(A ∩ B)
Ý nghĩa: Xác suất xảy ra đồng thời sự kiện A và B (A and B).
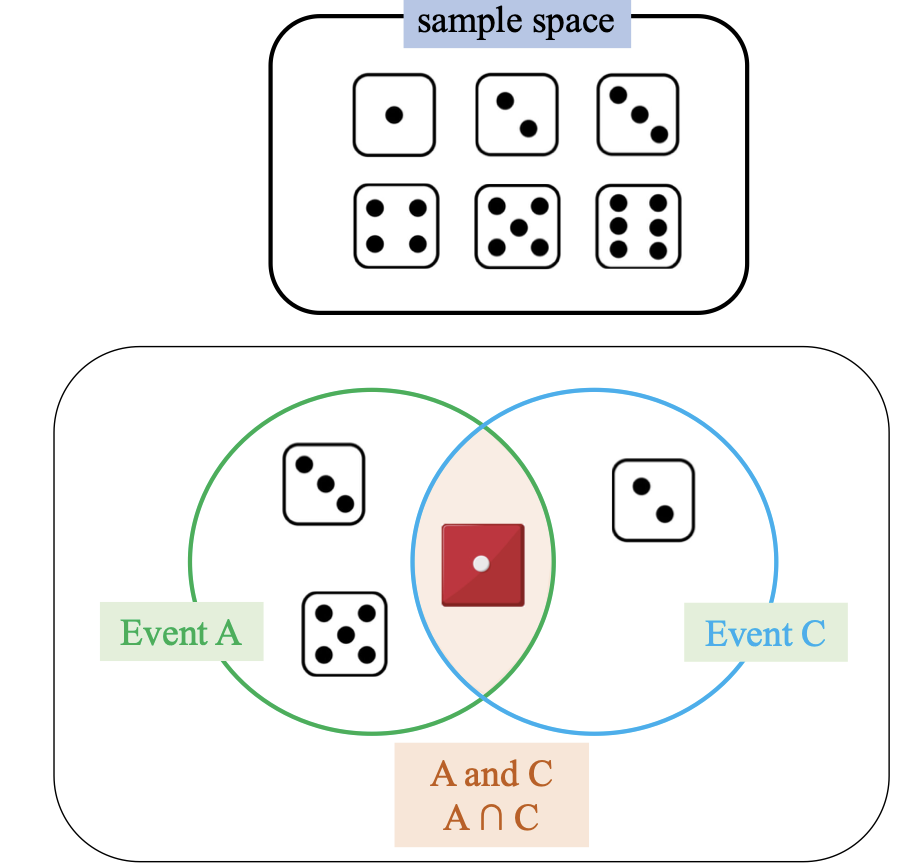
-
Nói cách khác: Đây là phần giao giữa hai tập con trong không gian mẫu.

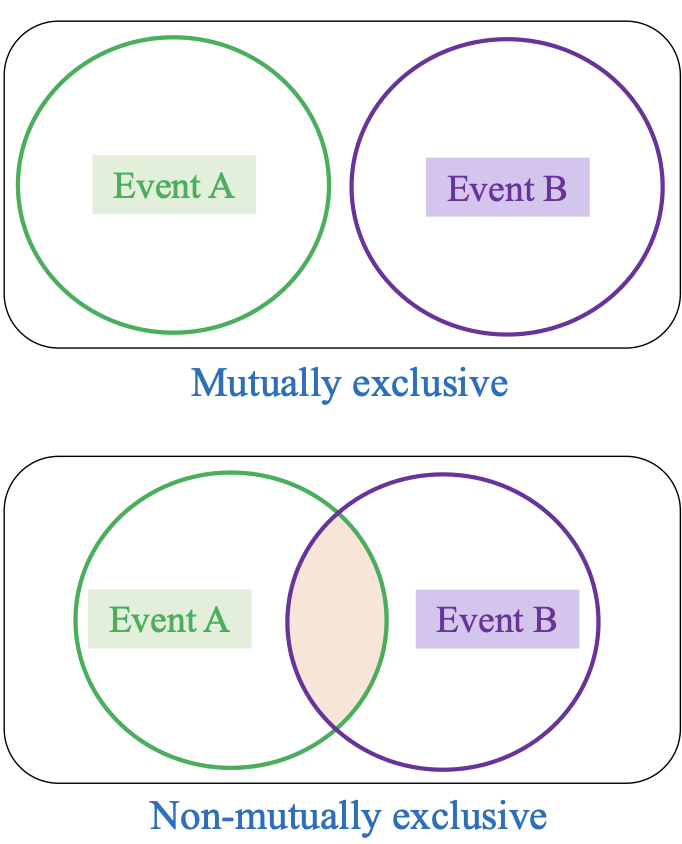
2.2 Mutually exclusive event
 Định nghĩa:
Sự kiện/Biến cố xung khắc (Mutually Exclusive Event): Hai sự kiện A và B được gọi là xung khắc (loại trừ lẫn nhau) nếu chúng không thể xảy ra đồng thời, tức là A ∩ B = ∅ hay P(A ∩ B) = 0.
Định nghĩa:
Sự kiện/Biến cố xung khắc (Mutually Exclusive Event): Hai sự kiện A và B được gọi là xung khắc (loại trừ lẫn nhau) nếu chúng không thể xảy ra đồng thời, tức là A ∩ B = ∅ hay P(A ∩ B) = 0.
- Ví dụ: Khi gieo một con xúc xắc, A là “ra số chẵn”, B là “ra số lẻ”. A và B là hai sự kiện xung khắc.
 Ký hiệu:
A∩B=∅(giao rỗng)
|Khái niệm|Ký hiệu|Kết luận|
|---|---|---|
|Mutually exclusive events|A∩B=∅|Không thể xảy ra đồng thời|
|Non-mutually exclusive events|A∩B≠∅|Có thể xảy ra đồng thời (có phần tử chung)|
Ký hiệu:
A∩B=∅(giao rỗng)
|Khái niệm|Ký hiệu|Kết luận|
|---|---|---|
|Mutually exclusive events|A∩B=∅|Không thể xảy ra đồng thời|
|Non-mutually exclusive events|A∩B≠∅|Có thể xảy ra đồng thời (có phần tử chung)|
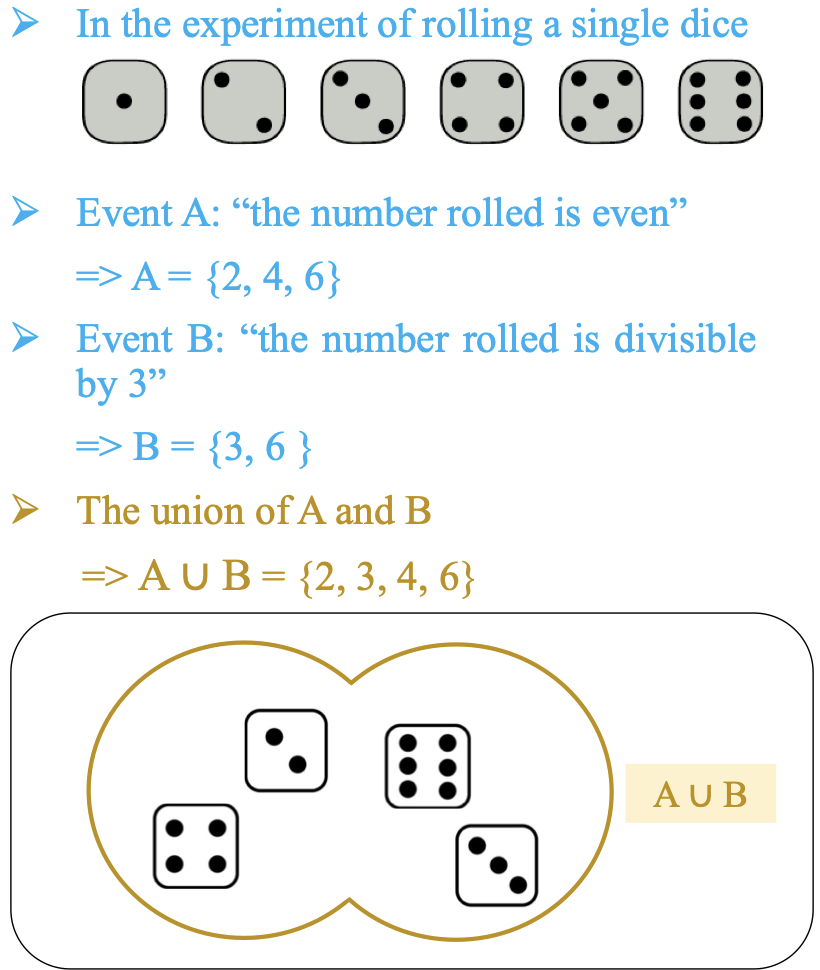
2.3 Union of events
Định nghĩa: Phép hợp (Union): là tập hợp các kết quả thuộc A, hoặc thuộc B, hoặc cả hai. Ký hiệu là (A ∪ B) hay (A or B).
- Tuy nhiên, cần lưu ý trong trường hợp các biến cố A và B có xung khắc hay không:
-
Nếu A và B là hai biến cố xung khắc:
P(A ∪ B) = P(A) + P(B)
-
Nếu A và B không xung khắc:
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
-
 Ký hiệu:
A∪B
Ký hiệu:
A∪B
| Phép toán | Ký hiệu | Ý nghĩa | Ví dụ kết quả |
|---|---|---|---|
| Giao (AND) | A∩B | Cả A và B | {2} |
| Hợp (OR) | A∪B | A hoặc B hoặc cả hai | {1,2,3,4,6} |
Từ khóa: “hoặc” (OR logic) — Chỉ cần thuộc một trong hai (hoặc cả hai) thì được đưa vào hợp.
2.4 Complement of an Event
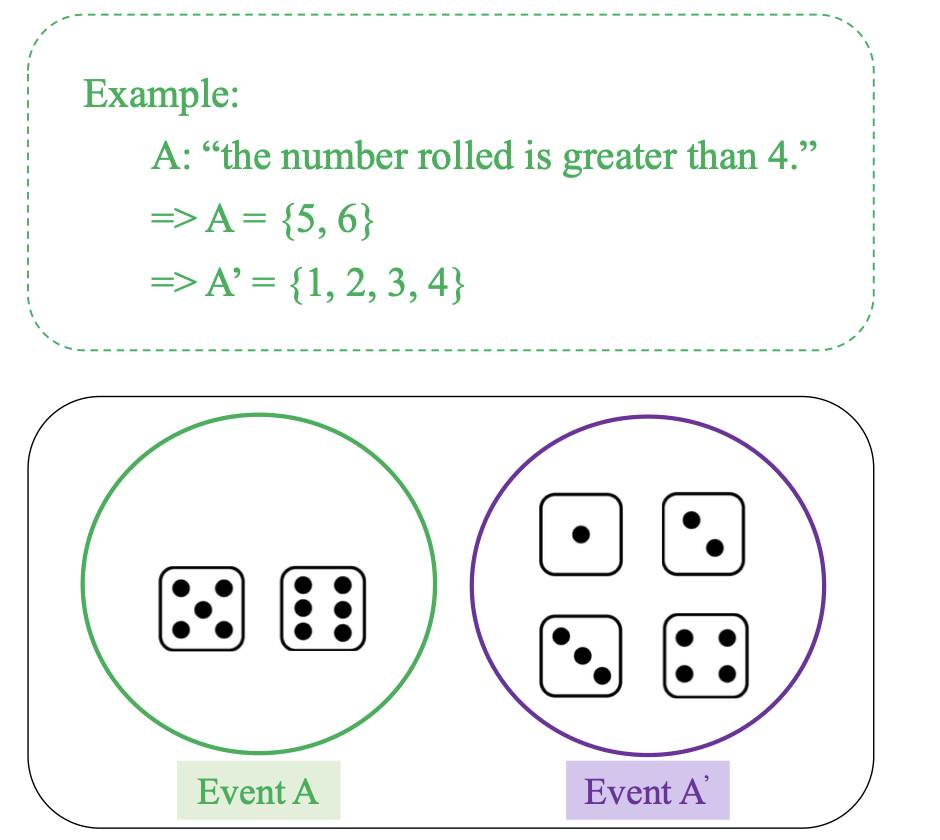
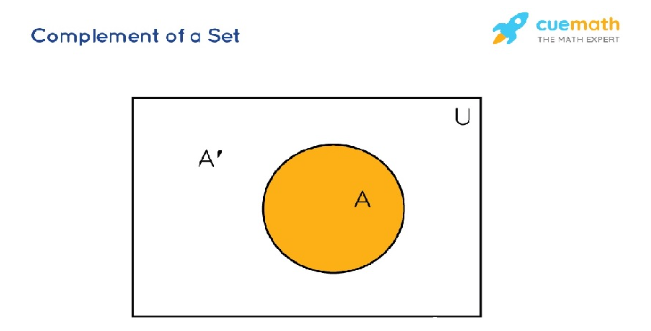 Phần bù (Complement): Phần bù của sự kiện A (ký hiệu A’ hoặc Aᶜ) là tập hợp các kết quả không thuộc A, với A + A’ = Ω và P(A) + P(A’) = 1.
Phần bù (Complement): Phần bù của sự kiện A (ký hiệu A’ hoặc Aᶜ) là tập hợp các kết quả không thuộc A, với A + A’ = Ω và P(A) + P(A’) = 1.
- Khi đó, A và A’ kết hợp tạo thành một hệ đầy đủ (complete system), chứa tất cả các kết quả có thể xảy ra trong không gian mẫu Ω.
- Bổ sung (complement) của một biến cố A, ký hiệu là:
-
A′ hoặc Ac hoặc A’
-
- Là tập hợp tất cả các kết quả trong không gian mẫu Ω mà không thuộc A.
- Ý nghĩa thực tế:
Nếu A là biến cố xảy ra, thì A′A′ là biến cố A không xảy ra.
III. Probability
Để diễn tả khả năng xảy ra của một sự kiện nào đó phục vụ cho việc tính toán toán học, ta sử dụng khái niệm xác suất, ký hiệu là P.
- Xác suất của một sự kiện là một số nằm trong khoảng từ 0 đến 1, với:
- P(Ω) = 1
- P(∅) = 0
- 0 biểu thị sự bất khả thi (sự kiện không thể xảy ra)
- 1 biểu thị sự chắc chắn (sự kiện chắc chắn xảy ra)
- Giá trị càng gần 1 thì sự kiện càng dễ xảy ra, càng gần 0 thì càng khó xảy ra. Ý nghĩa của giá trị xác suất: |Giá trị của P(A)|Ý nghĩa| |---|---| |P(A)=0|Biến cố không thể xảy ra (impossible event)| |0<P(A)<1|Biến cố có thể xảy ra (ngẫu nhiên)| |P(A)=1|Biến cố chắc chắn xảy ra (certain event)|
-
Classical Probability
Theo lý thuyết xác suất cổ điển, xác suất của một biến cố A được tính bằng cách lấy số lần biến cố A xảy ra chia cho tổng số lần xảy ra của tất cả các biến cố.

Ví dụ:
Xác suất rút trúng một lá bài chuồn trong một bộ bài 52 lá là:
P(chuồn) = 13 / 52 = 1 / 4
Ví dụ:
Biến cố Tập kết quả P(A) Ra số chẵn {2, 4, 6} 3/6 = 0.5 Ra số > 4 {5, 6} 2/6 = 1/3 Ra số < 3 {1, 2} 2/6 = 1/3 Ra số nguyên tố {2, 3, 5} 3/6 = 0.5 Ra số là 1 {1} 1/6 ≈ 0.1667 -
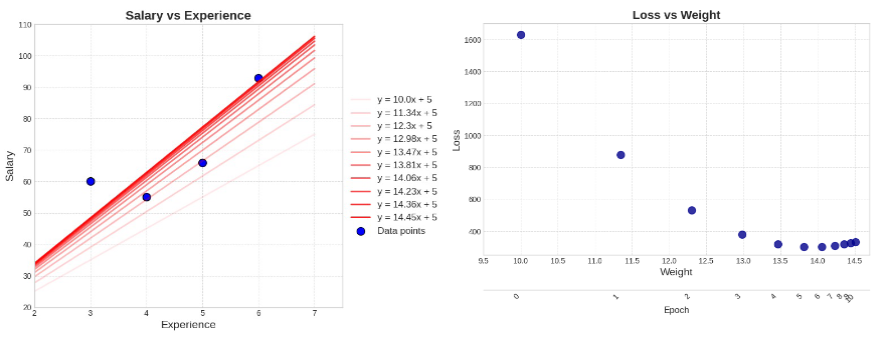
Geometric Probability Trong trường hợp các khả năng xảy ra là một biến liên tục, cách tính xác suất cổ điển không thể “đếm” được. Khi nào dùng?
- Khi biến ngẫu nhiên là liên tục, và không thể đếm được số kết quả riêng lẻ (như các số thực).
- Thay vì đếm số phần tử, ta đo chiều dài, diện tích hoặc thể tích.
Công thức xác suất hình học:
 Ví dụ minh họa:
Ví dụ minh họa:
Cho biết:
Một số ngẫu nhiên XX được chọn từ đoạn [0, 1] (liên tục, vô số giá trị thực).
Tính xác suất để XX nằm trong khoảng (0, 0.25). Giải:
-
Không gian mẫu: đoạn từ 0 đến 1
→ độ dài: 1−0= 1
-
Miền mong muốn (A): đoạn từ 0 đến 0.25
→ độ dài: 0.25−0=0.25
-
Áp dụng công thức: P(A)=0.25 / 1=0.25
Kết luận: Xác suất để X∈(0,0.25)X∈(0,0.25) là 0.25 hay 25%. |Dạng đo lường|Ví dụ thực tế| |---|---| |Độ dài (Length)|Số ngẫu nhiên trên đoạn [a, b]| |Diện tích (Area)|Bắn trúng mục tiêu hình tròn, hình vuông| |Thể tích (Volume)|Xác suất rơi vào 1 khối trong không gian|
-
Empirical Probability
Định nghĩa:
là xác suất của một sự kiện được xác định dựa trên kết quả thực tế của các lần thử nghiệm hoặc quan sát, thay vì dựa trên lý thuyết hoặc giả định toán học
Công thức:
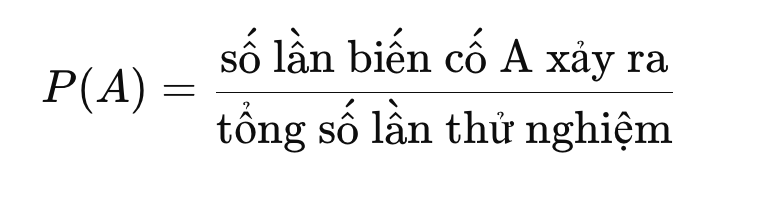
3.1 Rules of probability
-
The Additive Rule
Trường hợp 1: Biến cố xung khắc (mutually exclusive / disjoint)
Hai biến cố A và B không thể xảy ra đồng thời, tức:
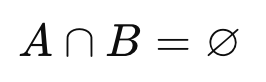
Khi đó:
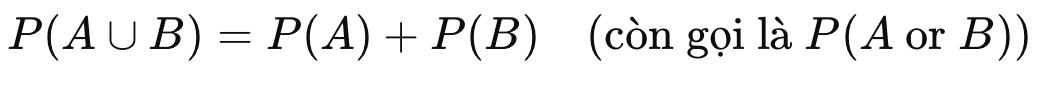
Trường hợp 2: Tổng quát (non-mutually exclusive)
Nếu A và B có thể xảy ra đồng thời, thì cần trừ phần giao:
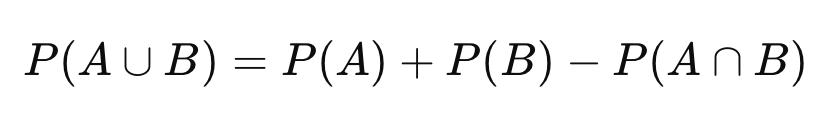
Trường hợp Công thức Khi nào dùng? Mutually exclusive (xung khắc) P(A∪B)=P(A)+P(B) A và B không thể xảy ra cùng lúc General case (có giao) P(A∪B)=P(A)+P(B)−P(A∩B) A và B có thể xảy ra đồng thời (có giao)
Ví dụ Gieo một viên xúc xắc công bằng. Xác suất để biến cố A = {3, 4} xảy ra là bao nhiêu?
-
Viên xúc xắc là công bằng ⇒ 6 kết quả có thể xảy ra đều có xác suất bằng nhau:
-
Các biến cố {1}, {2}, …, {6} là rời nhau (xung khắc – không thể xảy ra cùng lúc).
-
Tổng xác suất của toàn bộ không gian mẫu:
-
Vì {3} và {4} là rời nhau (mutually exclusive):
| Tên quy tắc | Công thức |
|---|---|
| Giới hạn | 0≤P(A)≤1 |
| Không gian mẫu | P(Ω)=1 |
| Biến cố rỗng | P(∅)=0 |
| Cộng (rời nhau) | P(A∪B)=P(A)+P(B) |
| Cộng (chung) | P(A∪B)=P(A)+P(B)−P(A∩B) |
| Nhân (độc lập) | P(A∩B)=P(A)⋅P(B) |
| Bù | P(Ac)=1−P(A) |
| Có điều kiện | P(A∣B)=P(A∩B)P(B) |
3.2 Conditional Probability
Định nghĩa:
Xác suất của biến cố AA, biết rằng biến cố BB đã xảy ra, được ký hiệu là:
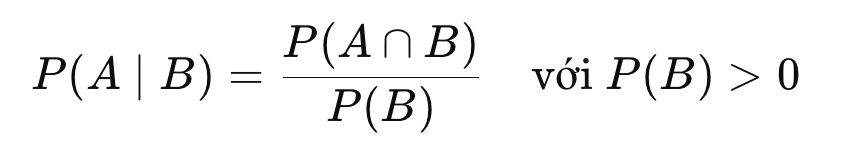 Ví dụ cụ thể:
Thí nghiệm: Gieo một viên xúc xắc công bằng
S={1,2,3,4,5,6}
➤ Bài toán:
Tìm xác suất số gieo được là 3, biết rằng số đó là số lẻ.
Xét các biến cố:
Ví dụ cụ thể:
Thí nghiệm: Gieo một viên xúc xắc công bằng
S={1,2,3,4,5,6}
➤ Bài toán:
Tìm xác suất số gieo được là 3, biết rằng số đó là số lẻ.
Xét các biến cố:
- Biến cố A: “số là 3” ⇒ A={3}A={3}
- Biến cố B: “số là số lẻ” ⇒ B={1,3,5}B={1,3,5}
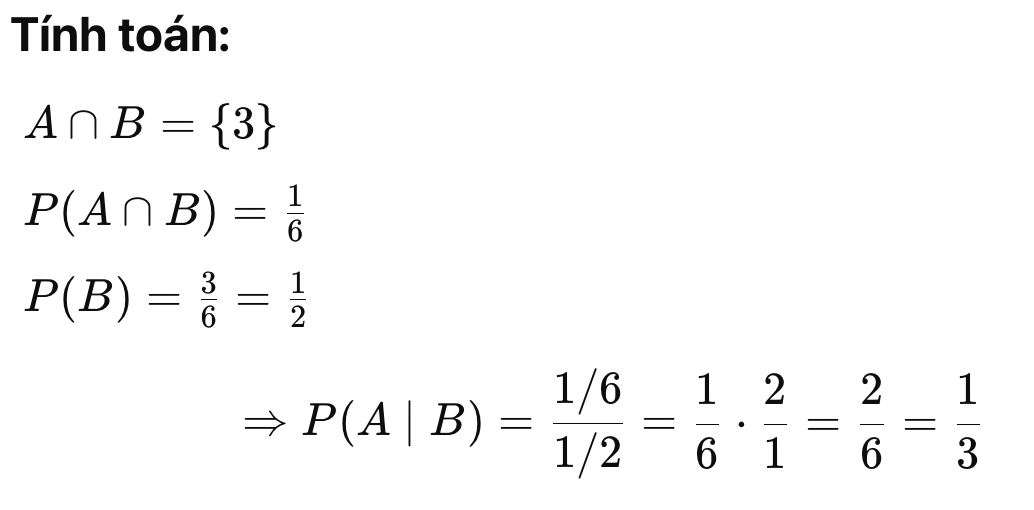
xác suất có điều kiện
với 2 câu hỏi đảo ngược lẫn nhau. Đây là một cách tuyệt vời để hiểu rõ bản chất của P(A∣B) và P(B∣A), vì chúng không giống nhau
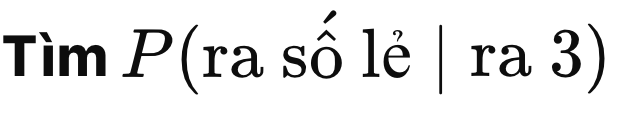
. |Câu hỏi|Kết quả|Ý nghĩa| |---|---|---| |a) P(3| số lẻ)|13|Trong các số lẻ, có 1/3 là số 3| |b) P(số lẻ | 3)|1|Nếu biết là ra 3, thì chắc chắn là số lẻ|
3.3 Multiplication Rule
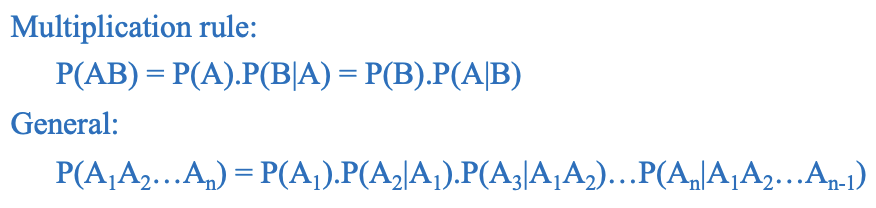 Tóm tắt đề bài:
Tóm tắt đề bài:
- Có 10 chìa khoá giống hệt nhau, trong đó 2 chìa đúng (mở được cửa), còn 8 chìa sai (không mở được).
- Ta chọn ngẫu nhiên từng chìa, thử, và loại bỏ nếu không mở được.
- Câu hỏi: Xác suất cửa được mở đúng vào lần thử thứ 3? Hiểu bản chất yêu cầu:
- 2 chìa đúng, 8 chìa sai.
- Cửa chỉ được mở ở lần thử thứ 3 nghĩa là:
- Lần 1: chọn chìa sai
- Lần 2: chọn chìa sai
- Lần 3: chọn chìa đúng
Dùng Multiplication Rule:
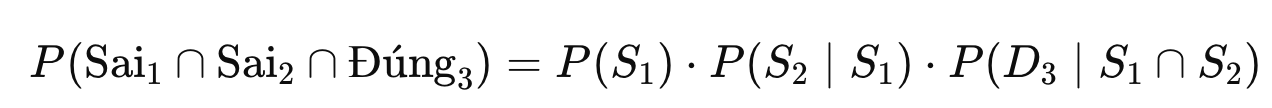
 Tổng xác suất:
Tổng xác suất:
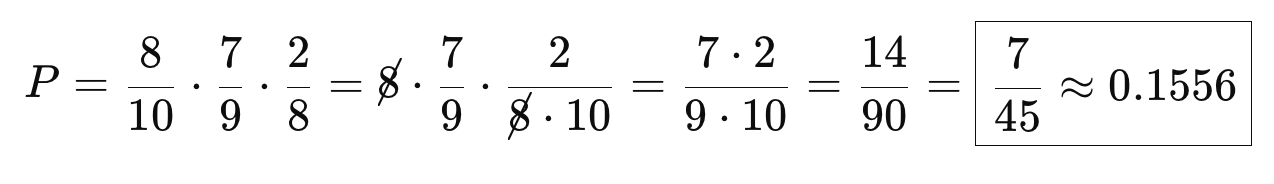
3.4 Independent events
Hai biến cố A và B được gọi là độc lập nếu:
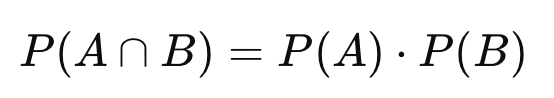 Nghĩa là việc xảy ra của biến cố A không ảnh hưởng gì đến xác suất xảy ra của biến cố B, và ngược lại.
Ví dụ bạn đưa ra:
Nghĩa là việc xảy ra của biến cố A không ảnh hưởng gì đến xác suất xảy ra của biến cố B, và ngược lại.
Ví dụ bạn đưa ra:
- Không gian mẫu khi gieo 1 viên xúc xắc: S={1,2,3,4,5,6} Xét các biến cố:
- A={4}A={4}
- B={2,4,6}
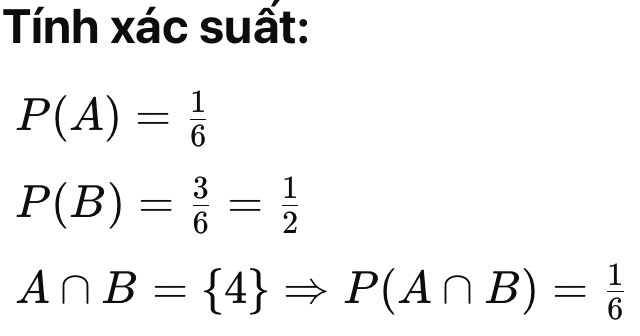 Kiểm tra điều kiện độc lập:
Kiểm tra điều kiện độc lập:
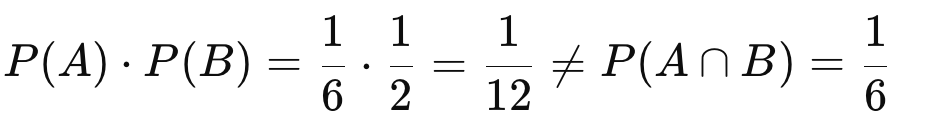 → Sai lệch → A và B không độc lập, hay còn gọi là phụ thuộc (dependent).
Ý nghĩa trực quan:
→ Sai lệch → A và B không độc lập, hay còn gọi là phụ thuộc (dependent).
Ý nghĩa trực quan: - Nếu bạn biết trước rằng B xảy ra (ra số chẵn), thì khả năng A xảy ra tăng lên (vì 4 nằm trong B).
- Do đó, A và B không độc lập — việc biết B xảy ra làm thay đổi xác suất của A. |Trường hợp|Kết luận| |---|---| |P(A∩B)=P(A)P(B)|A và B độc lập| |P(A∩B)≠P(A)P(B)|A và B phụ thuộc|
IV. Bayes’ Theorem
-
Total Probability Theorem
Phát biểu:

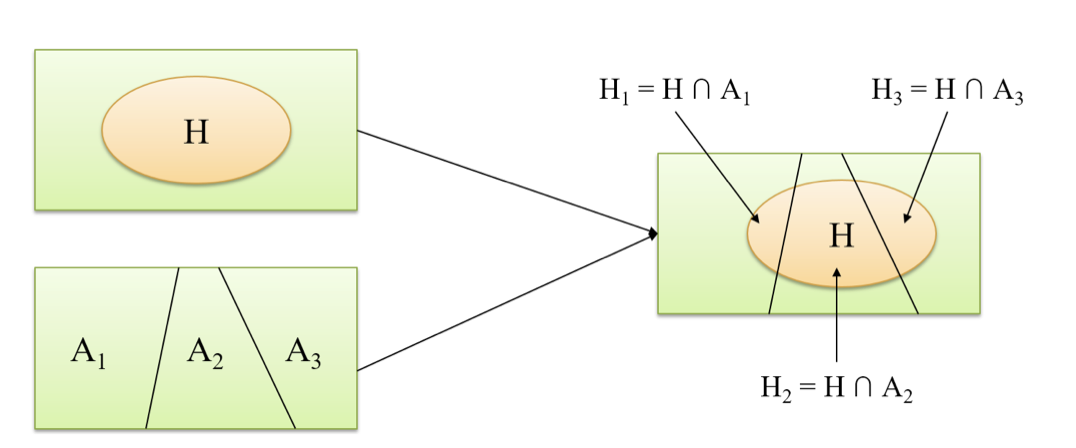
Ví dụ minh họa: Tình huống: Một nhà máy có 3 dây chuyền sản xuất:
-
A1: Dây chuyền 1 sản xuất 50% sản phẩm
-
A2: Dây chuyền 2 sản xuất 30%
-
A3: Dây chuyền 3 sản xuất 20% Xác suất sản phẩm lỗi:
-
P(H|A1)=0.01
-
P(H|A2)=0.02
-
P(H|A3)=0.05 Áp dụng công thức:
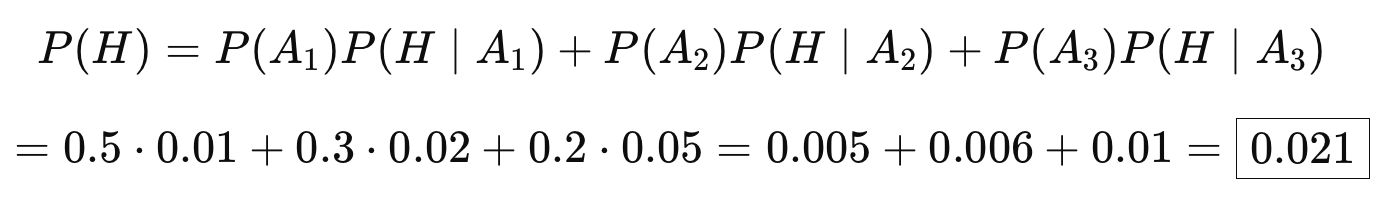 Tình huống:
Tình huống:
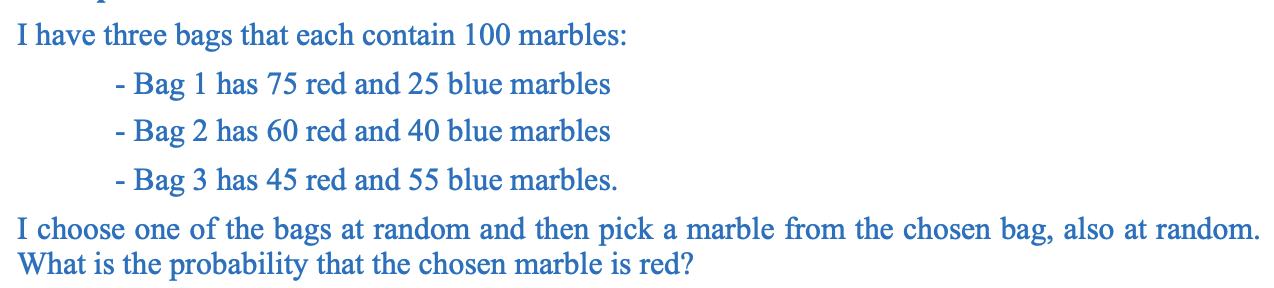 Có 3 túi bi (Bag I, II, III).
Mỗi túi có 100 viên bi, và chọn ngẫu nhiên một túi rồi lấy 1 viên bi từ túi đó.
Có 3 túi bi (Bag I, II, III).
Mỗi túi có 100 viên bi, và chọn ngẫu nhiên một túi rồi lấy 1 viên bi từ túi đó. -
A1: Chọn túi 1
-
A2: Chọn túi 2
-
A3: Chọn túi 3
→ Các sự kiện A1,A2,A3 tạo thành một hệ phân hoạch đầy đủ của không gian mẫu)

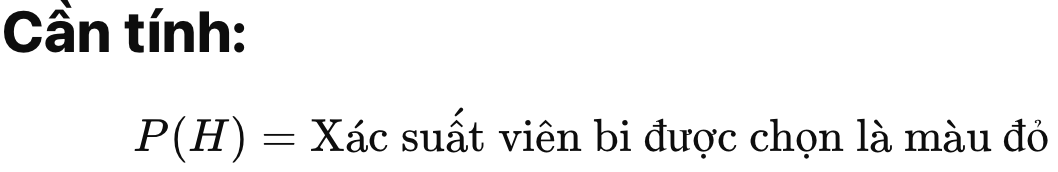
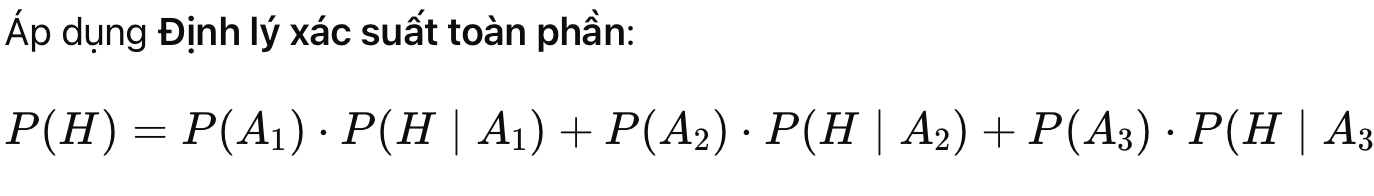
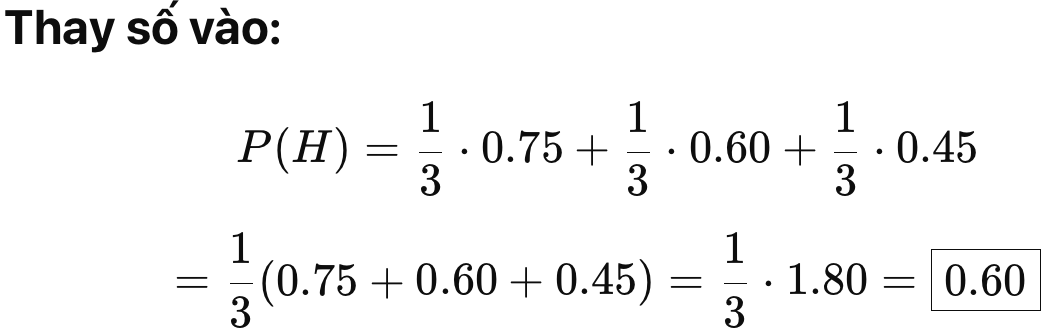
3.1 Bayes’ Rule
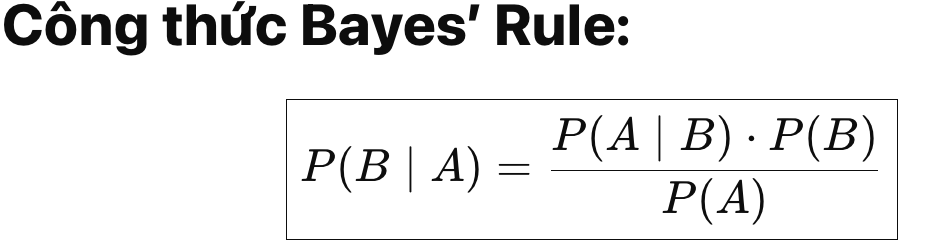
| Thành phần | Ý nghĩa |
|---|---|
| P(B∣A) | Xác suất hậu nghiệm (posterior): Xác suất B đúng khi biết A đúng |
| P(A∣B) | Độ tin cậy / khả năng xảy ra (likelihood): Xác suất A xảy ra nếu B đúng |
| P(B) | Xác suất tiên nghiệm (prior): Xác suất B đúng trước khi biết gì thêm |
| P(A) | Xác suất cận biên (marginal): Xác suất A đúng (tổng xác suất tất cả trường hợp) |
| Bayes giúp bạn cập nhật niềm tin về một giả thuyết (B), khi bạn có bằng chứng (A). | |
| Tóm tắt sơ đồ tư duy Bayes: |
- Prior → Kiến thức trước (niềm tin ban đầu)
- Likelihood → Bằng chứng bạn quan sát được
- Marginal → Tổng xác suất bằng chứng xảy ra (tính bằng Định lý xác suất toàn phần)
- Posterior → Niềm tin cập nhật sau khi thấy bằng chứng

Biết rằng viên bi chọn ra là đỏ, hỏi: xác suất nó đến từ túi 1 là bao nhiêu?
Áp dụng Bayes:

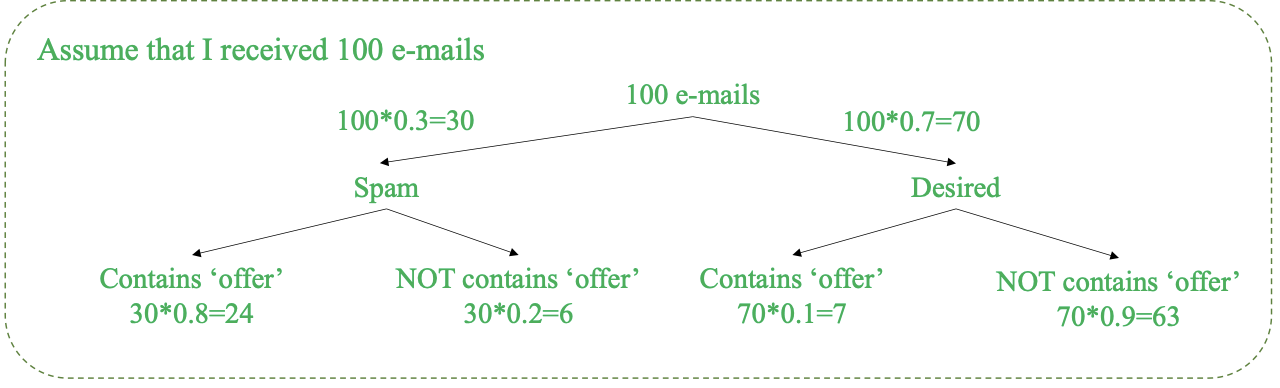
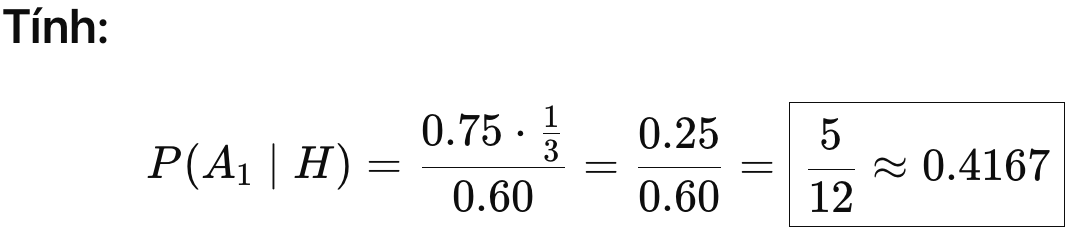 Xác suất một email là spam nếu chứa từ “offer”?
Tóm tắt bài toán:
Xác suất một email là spam nếu chứa từ “offer”?
Tóm tắt bài toán:
-
S: Email là spam
-
H: Email chứa từ “offer”

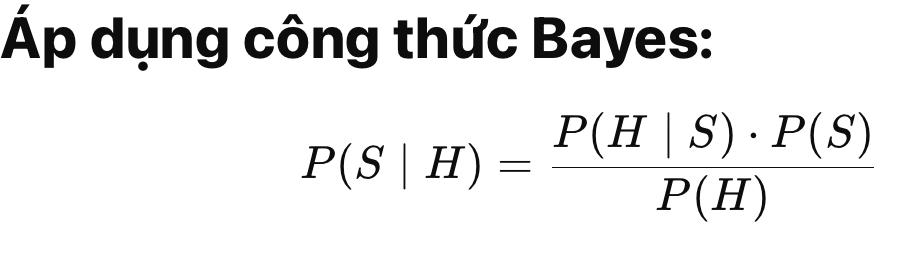 Tính mẫu số P(H) (xác suất thấy từ “offer” trong bất kỳ email nào):
Tính mẫu số P(H) (xác suất thấy từ “offer” trong bất kỳ email nào):