Giới thiệu

Table of Content

Tham khảo
Giới thiệu
I. Basic Descriptive Statistics
- 1. Population Mean
- 2. Sample Mean
- 3. Degrees of Freedom
  - Định nghĩa gốc
  - Kể chuyện đồng xu
  - Đối với Sample Mean
  - [[#tại-sao-phương-sai-mẫu-chia-cho-import-urlhttpscdnjscloudflarecomajaxlibskatex0169katexmincssn1n1n1|Tại sao phương sai mẫu chia cho @import url(‘https://cdnjs.cloudflare.com/ajax/libs/KaTeX/0.16.9/katex.min.css’)n−1n−1n−1?]]
II. Advance Descriptive Statistics
III. Applications
- 1. Application to Patch Matching
  - Cơ chế
  - Template matching
- 2. Object Detection

I. Basic Descriptive Statistics

1. Population Mean

2. Sample Mean

3. Degrees of Freedom

Định nghĩa gốc

Trong thống kê, số bậc tự do (degrees of freedom, viết tắt là df) chính là số lượng giá trị trong phép tính cuối cùng còn tự do thay đổi. Nói cách khác, đó là số thông tin thực sự độc lập mà bạn có thể biết trước khi mọi thứ còn lại đều đã bị cố định bởi ràng buộc toán học.

Kể chuyện đồng xu

Hãy tưởng tượng bạn tung một đồng xu 100 lần.
Kết quả mỗi lần chỉ có 2 khả năng: Head hoặc Tail.
Nếu bạn muốn biết tôi ra bao nhiêu mặt ngửa (head) và bao nhiêu mặt sấp (tail), bạn chỉ cần hỏi 1 thông tin: “Có bao nhiêu lần ra mặt head?”
Vì nếu biết số lần ra head, bạn sẽ biết ngay số lần ra tail = 100 – số lần ra head. ⇒ Chỉ cần 1 thông tin (1 degree of freedom) là đủ để xác định toàn bộ kết quả. Với xúc xắc 6 mặt, tung 10 lần – bậc tự do là bao nhiêu?
Nếu bạn biết số lần ra 5 mặt đầu tiên, số lần tung ở mặt còn lại chắc chắn bạn sẽ biết. Đó gọi là bậc tự do. → Mặt còn lại bị phụ thuộc vào 5 giá trị kia nên Không tự do.

Đối với Sample Mean

Từ đó khi đã biết trước trung bình mẫu, giá trị cuối cùng trong mẫu không còn tự do lựa chọn nữa – nó bị ràng buộc để đảm bảo tổng số vẫn đúng.
Ví dụ: Bạn có một bộ ba số, biết hai số đầu là 4 và 5, và biết trung bình của cả ba số là 5. Vậy số thứ ba là gì?

Tổng ba số: $3 \times 5 = 15$
Số cuối: $15 - 4 - 5 = 6$ Rõ ràng, khi đã biết trung bình, giá trị cuối cùng bị “khóa cứng” – không thể tự do (independence) nữa. ⇒ Chỉ còn (n-1) giá trị là tự do (bậc tự do).

Tại sao phương sai mẫu chia cho $n - 1$ ?

Khi ước lượng phương sai từ mẫu, công thức là: $var (X) = \frac{1}{n - 1} \sum_{k = 1}^{n} (x_{k} - \overset{x}{ˉ})^{2}$

Mẫu số là $n - 1$ , chứ không phải $n$ , vì:
- Đã dùng hết 1 bậc tự do để xác định trung bình mẫu, còn lại $n - 1$ bậc tự do cho các giá trị còn lại. Nếu chia cho $n$ , bạn đã giả định rằng trung bình mẫu là trung bình đúng của toàn bộ tổng thể (population mean), nhưng thực tế trung bình mẫu có thể khác, gây thiên lệch (bias). Việc chia cho $n - 1$ giúp điều chỉnh thiên lệch đó, tạo ra một ước lượng phương sai không chệch.

II. Advance Descriptive Statistics

1. Correlation

Correlation vs Regression

Correlation (Tương quan):

Là phép đo mức độ liên hệ hoặc mức độ đồng biến động giữa hai biến số.
Hỏi: “Hai biến này có liên quan đến nhau không? Nếu một biến tăng, biến kia có xu hướng tăng/giảm không?”
Không phân biệt nguyên nhân – kết quả.
Ví dụ: Điểm Toán và điểm Lý của học sinh cùng lớp – điểm cao Toán thì thường cao Lý, đó là có tương quan.
Công thức: hệ số tương quan Pearson:

Regression (Hồi quy):

Mô tả mối quan hệ định lượng: Biến độc lập (independent variable) thay đổi gây ảnh hưởng như thế nào lên biến phụ thuộc (dependent variable).
Hỏi: “Nếu biết điểm Toán, có dự đoán được điểm Lý không? Nếu điểm Toán tăng 1 đơn vị, điểm Lý thay đổi bao nhiêu?”
Có phân biệt nguyên nhân – kết quả (predictor & outcome).
Ví dụ: Dự đoán lương (biến phụ thuộc) dựa vào số năm kinh nghiệm (biến độc lập).
Công thức: $y = β_{0} + β_{1} x + ϵ$ Trong đó:

Correlation Between Two Variables

Tương quan dương hoàn hảo (Correlation ≈ +1)

Dữ liệu:

X: 1, 2, 3, 4, 5, 6

Y: 2, 4, 6, 8, 10, 12
Đặc điểm: Khi X tăng, Y tăng tỷ lệ thuận và mọi điểm nằm trên một đường thẳng.
Ý nghĩa: Hệ số tương quan gần bằng +1, thể hiện mối liên hệ mạnh nhất, tuyến tính tuyệt đối.
Ví dụ thực tế: Mua 1 cuốn sách giá 20k, mua 2 cuốn giá 40k,… (giá tăng tuyệt đối theo số lượng).

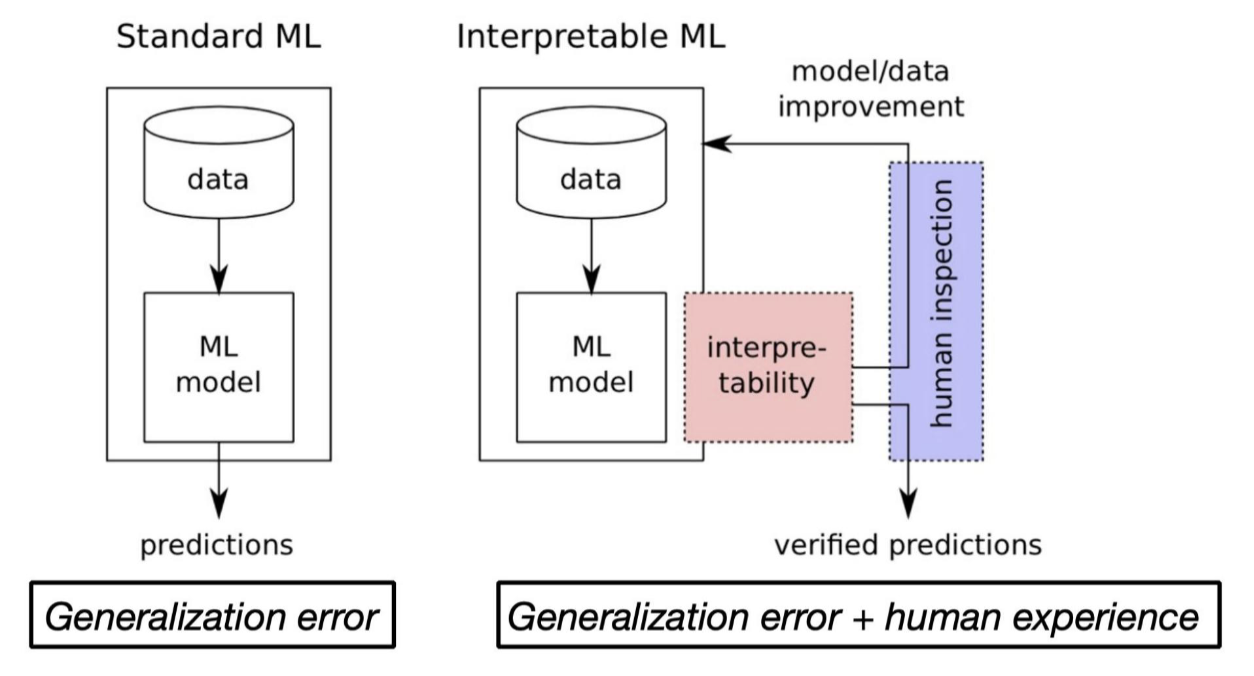image 53.png Tương quan âm hoàn hảo (Correlation ≈ -1)

Dữ liệu:

X: 1, 2, 3, 4, 5, 6

Y: 12, 10, 8, 6, 4, 2
Đặc điểm: Khi X tăng, Y giảm tỷ lệ thuận, mọi điểm cũng nằm trên một đường thẳng nhưng dốc xuống.
Ý nghĩa: Hệ số tương quan gần bằng -1, mối quan hệ tuyến tính nghịch đảo hoàn hảo.
Ví dụ thực tế: Số lượng bánh còn lại sau mỗi lần ăn: càng ăn nhiều (X tăng), bánh càng ít (Y giảm). 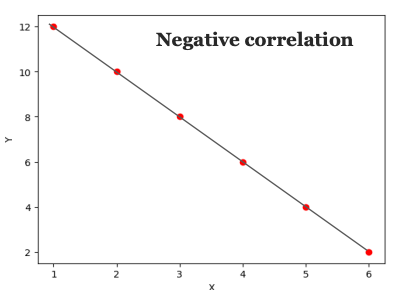Tương quan dương không hoàn hảo (0 < Correlation < 1) Dữ liệu: X: 1, 2, 3, 4, 5, 6 Y: 2, 6, 7, 9, 13, 14 Đặc điểm: Khi X tăng, Y cũng tăng, nhưng không phải tất cả điểm đều nằm trên một đường thẳng. Sự tăng trưởng có thể nhanh hoặc chậm khác nhau ở từng điểm. Ý nghĩa: Hệ số tương quan dương, nhưng nhỏ hơn 1, mối liên hệ tích cực nhưng không tuyệt đối. Có thể có yếu tố ngẫu nhiên/tác động ngoài ảnh hưởng. Ví dụ thực tế: Điểm số học sinh tăng khi học nhiều hơn, nhưng không phải ai học nhiều cũng tăng đều (còn do năng lực, sức khoẻ…).

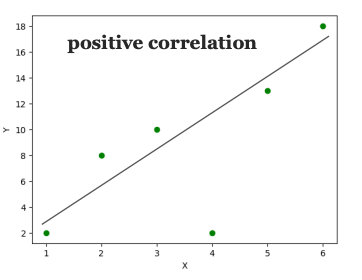image 2 20.png Tóm lại: Tương quan là thước đo mức độ và chiều hướng mà hai biến số thay đổi cùng nhau.

Nếu một biến tăng, biến còn lại cũng tăng → tương quan dương (positive).
Nếu một biến tăng, biến còn lại giảm → tương quan âm (negative).
Nếu một biến thay đổi, biến còn lại không thay đổi gì → không có tương quan (no correlation).

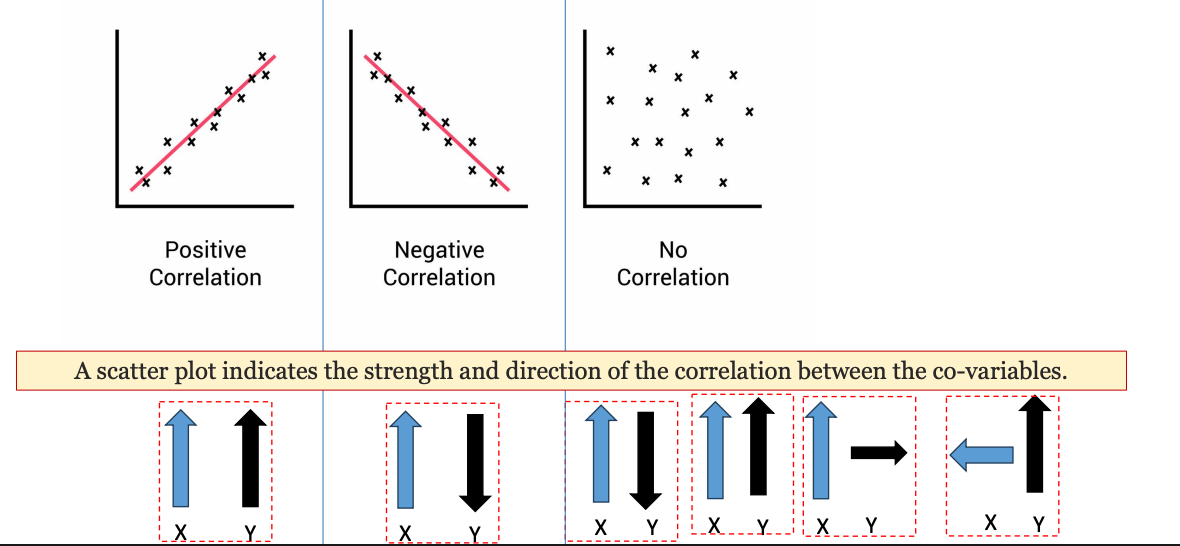
image 3 20.png

2. Correlation

3. Correlation vs Causation

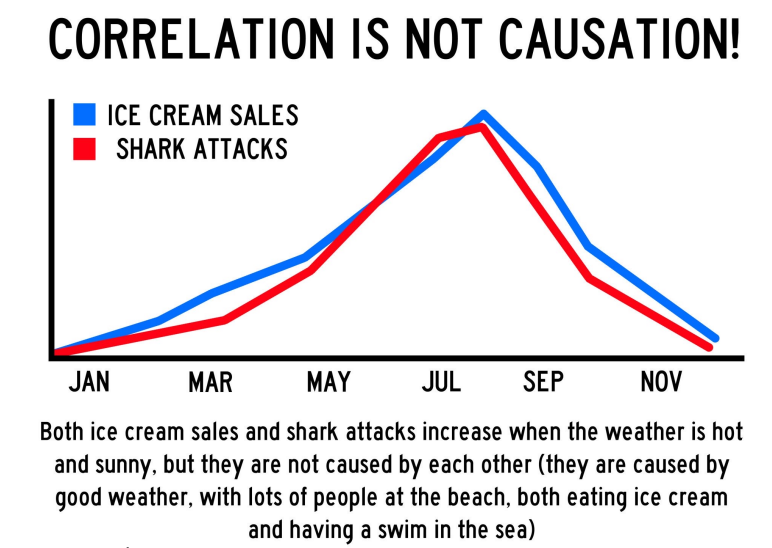
Tương quan không phải là quan hệ nhân quả!

Câu chuyện thú vị: Kem và cá mập image 4 16.png

Bạn thấy rằng doanh số bán kem và số vụ cá mập tấn công đều tăng vọt vào mùa hè, giảm vào mùa đông.
Nhìn biểu đồ, hai đường tăng-giảm gần như song song → tương quan dương rất mạnh.
Nhưng… liệu ăn kem có khiến cá mập tấn công nhiều hơn không?

Đáp án: KHÔNG!

2. Covariance - Hiệp phương sai

Review Variance

What is Covariance

Hãy tưởng tượng bạn đi khảo sát các siêu thị ở 5 thành phố (Hà Nội, Hồ Chí Minh, Cần Thơ, Đà Nẵng, Bình Định) và đếm số lượng táo xanh, táo đỏ ở mỗi nơi. Bảng số liệu thu được:

	Green apple	Red apple
Ha Noi	5	12
Ho Chi Minh	15	10
Can Tho	18	28
Da Nang	25	38
Binh Dinh	29	33

Trung bình táo xanh: 18.4
Trung bình táo đỏ: 24.2

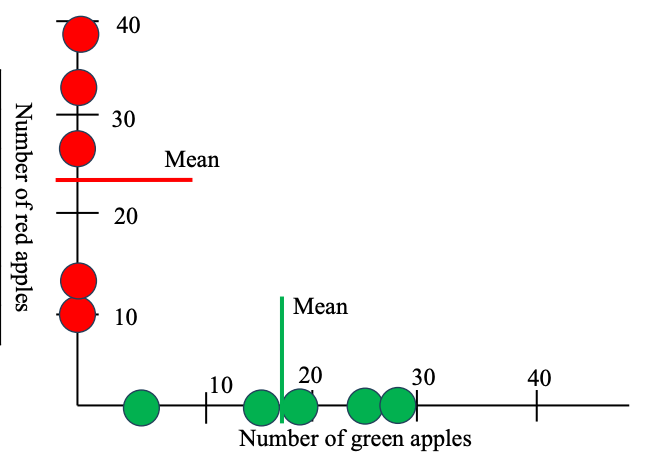
image 5 14.png

Mỗi siêu thị là một điểm trên biểu đồ (tọa độ: số táo xanh, số táo đỏ).
Đường ngang/thẳng đứng là giá trị trung bình của từng loại táo.
Nhìn hình: Khi siêu thị có nhiều táo xanh thường cũng có nhiều táo đỏ (điểm nằm cùng phía so với trung bình). 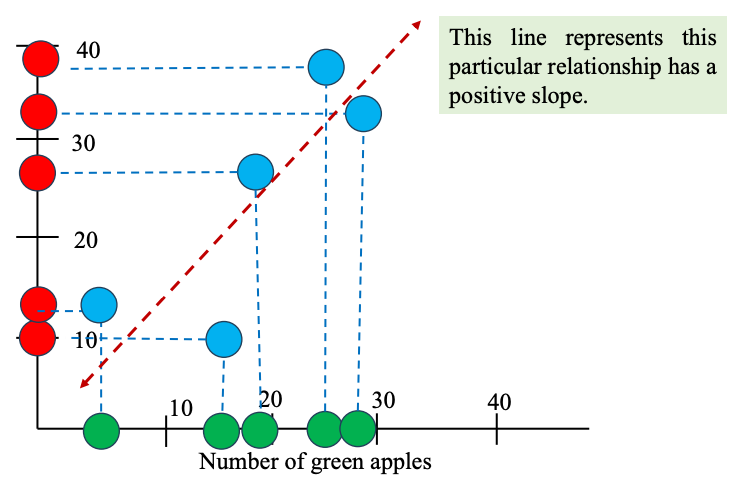Khi bạn đo lường một hiện tượng qua hai biến (ví dụ: số táo xanh và số táo đỏ ở các siêu thị), mỗi biến một mình chỉ cho biết trung bình, mức biến động… nhưng không nói gì về mối liên hệ giữa hai biến đó. Liệu các cặp giá trị này, khi ghép lại, có tiết lộ điều gì mà từng biến riêng lẻ không thể hiện ra không?

Covariance (hiệp phương sai) đo xem hai biến số (ở đây là số táo xanh và số táo đỏ) thay đổi cùng chiều hay ngược chiều khi so với giá trị trung bình của chính nó.

Nếu cùng lệch về một phía (cả hai đều nhiều hơn hoặc ít hơn trung bình) → covariance dương.
Nếu một cái tăng, một cái giảm (một hơn trung bình, một kém trung bình) → covariance âm.

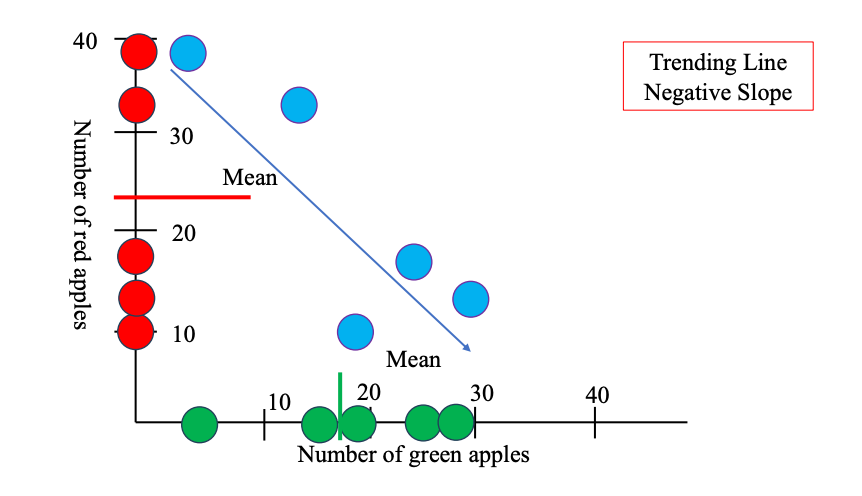
Ý nghĩa: Lúc này khi ta người ta cho biết số lượng táo xanh ở một tỉnh vd như Tây Ninh cao tầm 40 thì từ trend trên ta có thể dự đoán số lượng táo đỏ bán ra ở Tây Ninh cũng cao tầm 40. Khác dạng xu hướng khác: image 7 11.png

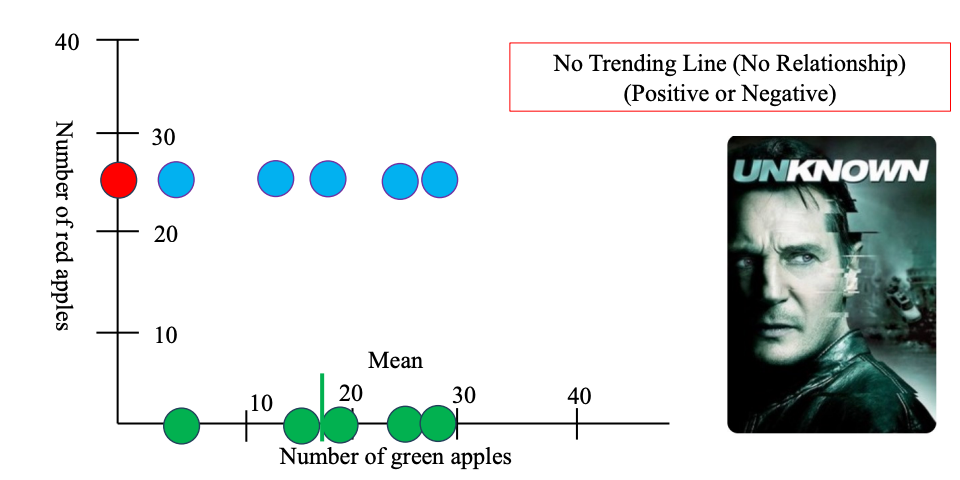image 8 11.png Nếu số lượng táo xanh ở mỗi siêu thị thay đổi không có quy luật gì với số lượng táo đỏ, thì:

Có siêu thị nhiều táo xanh nhưng táo đỏ ít, có nơi ngược lại, hoặc mỗi loại biến động không liên quan đến nhau.
Trên đồ thị scatter plot: các điểm phân bố ngẫu nhiên, không tạo thành một đường xu hướng nào (dốc lên hoặc dốc xuống). → Từ đó chúng ta không thể nào dự đoán được mối quan hệ giữa số lượng hai loại táo.

Ý tưởng chính của Covariance là làm sao nhận biết được 3 mối liên hệ này giữa Táo Xanh và Táo Đỏ Công thức

For Population: $Cov (X, Y) = \frac{1}{n} \sum_{i = 1}^{n} (x_{i} - \overset{x}{ˉ}) (y_{i} - \overset{y}{ˉ})$
For Sample: $Cov (X, Y) = \frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \overset{x}{ˉ}) (y_{i} - \overset{y}{ˉ})$ Trong đó:
$x_{i}$ : số táo xanh ở siêu thị iii
$y_{i}$ : số táo đỏ ở siêu thị iii
$\overset{x}{ˉ}, \overset{y}{ˉ}$ : trung bình mỗi loại táo Covariance dương (> 0):
Khi một biến tăng, biến còn lại cũng có xu hướng tăng.
Khi một biến giảm, biến còn lại cũng giảm.
Ví dụ: Nhiệt độ ngoài trời và lượng kem bán ra – càng nóng càng bán được nhiều kem. Covariance âm (< 0):
Khi một biến tăng, biến còn lại có xu hướng giảm.
Ngược lại, khi một biến giảm, biến còn lại tăng.
Ví dụ: Số giờ xem TV và điểm số học tập – càng xem TV nhiều, điểm số có thể càng giảm. Covariance gần bằng 0:
Hai biến thay đổi không liên quan gì đến nhau.
Biết biến này không giúp dự đoán biến kia.
Ví dụ: Số lượng táo xanh và số học sinh đi học bằng xe đạp trong cùng một trường – không có mối liên hệ rõ ràng. 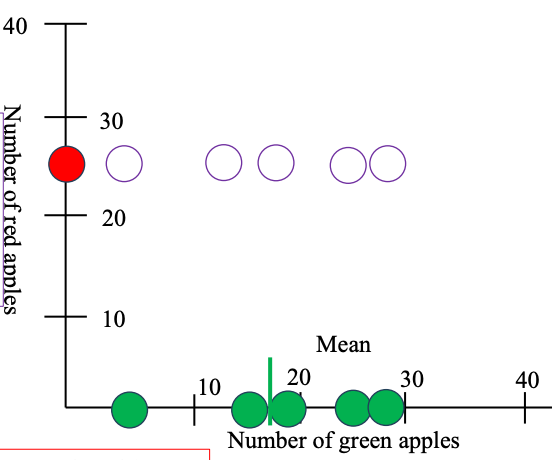Ta thấy Mean của táo đỏ chính là giá trị của những quả táo đỏ nên trừ nhau sẽ = 0

Các vấn đề của Covariance

Tuy nhiên Covariance khá là khó để giải thích, trực quan cho người khác hiểu và có một vài vấn đề:

Giá trị covariance chỉ báo hiệu hai biến cùng chiều, ngược chiều hay không liên hệ – nhưng không nói gì về độ dốc của đường xu hướng (slope). 2. Giá trị covariance phụ thuộc trực tiếp vào đơn vị và độ lớn của dữ liệu:
Nếu bạn thay đổi đơn vị đo của một (hoặc cả hai) biến, covariance sẽ thay đổi theo, thậm chí có thể tăng hoặc giảm rất nhiều lần.

Ví dụ: Bạn có hai danh sách số lượng táo xanh ở các siêu thị:

Danh sách 1: [5, 15, 18, 25, 29]
Danh sách 2: [5, 15, 18, 25, 29] (giống nhau) Tính covariance:

import numpy as np
y = [5, 15, 18, 25, 29]
x = [5, 15, 18, 25, 29]
covariance = np.cov(x, y)[0][1]
print(np.round(covariance, 2))  # Kết quả: 86.8

Nếu bạn gấp đôi tất cả giá trị

Danh sách mới: [10, 30, 36, 50, 58]
Thực chất chỉ là đổi đơn vị đo, ví dụ từ “số trái” sang “cân” hoặc nhân đôi số lượng do lỗi nhập liệu. Tính lại covariance:

y = [5*2, 15*2, 18*2, 25*2, 29*2]
x = [5*2, 15*2, 18*2, 25*2, 29*2]
covariance = np.cov(x, y)[0][1]
print(np.round(covariance, 2))  # Kết quả: 347.2

→ Kết quả covariance tăng lên gấp 4 lần! Điều này làm cho covariance không thể dùng để so sánh sức mạnh liên hệ giữa các cặp biến khác nhau về đơn vị hoặc scale.

2. Correlation Coefficient

Covariance chỉ cho biết hai biến thay đổi cùng chiều hay ngược chiều, nhưng khó hiểu về mức độ mạnh/yếu:

Giá trị có thể rất lớn, rất nhỏ, hoặc âm/dương tuỳ thuộc đơn vị đo.
Không có “thang điểm chung” cho mọi bài toán. Nhưng… Covariance lại là “bước trung gian” quan trọng để tính toán các chỉ số khác như hệ số tương quan (correlation coefficient), phân tích thành phần chính (PCA), v.v.

Đặc điểm

Hệ số tương quan (ký hiệu $r$ ) là dạng chuẩn hóa của covariance:

Miền giá trị: từ 1 đến 1.
Diễn giải rõ ràng:
- $r = 1$ : liên hệ dương tuyệt đối (cùng tăng/giảm hoàn hảo).
- $r = - 1$ : liên hệ âm tuyệt đối (một tăng, một giảm hoàn hảo).
- $r = 0$ : không liên hệ.
- $∣ r ∣$ càng gần 1: liên hệ càng mạnh.
- $∣ r ∣$ càng gần 0: liên hệ càng yếu.

Vì sao correlation “xịn” hơn covariance?

Dễ so sánh:

Bạn có thể so sánh sức mạnh liên hệ giữa bất kỳ cặp biến nào, dù đơn vị đo hoàn toàn khác nhau.
Không nhạy cảm với scale:

Dù đổi đơn vị (cm → m, kg → g, số lượng → doanh thu), giá trị hệ số tương quan không đổi.

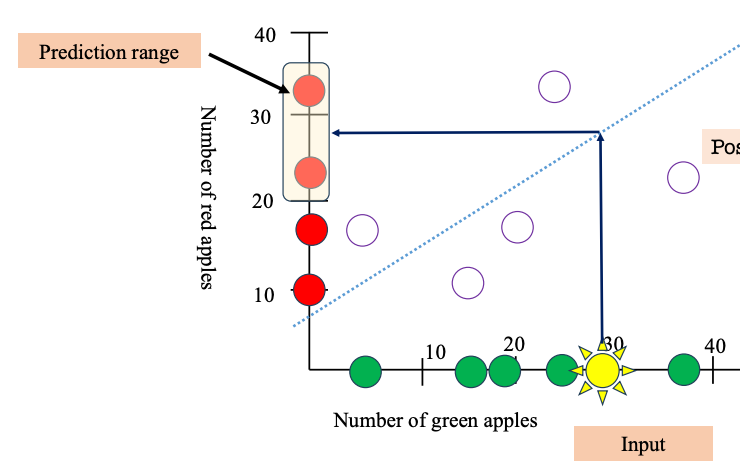
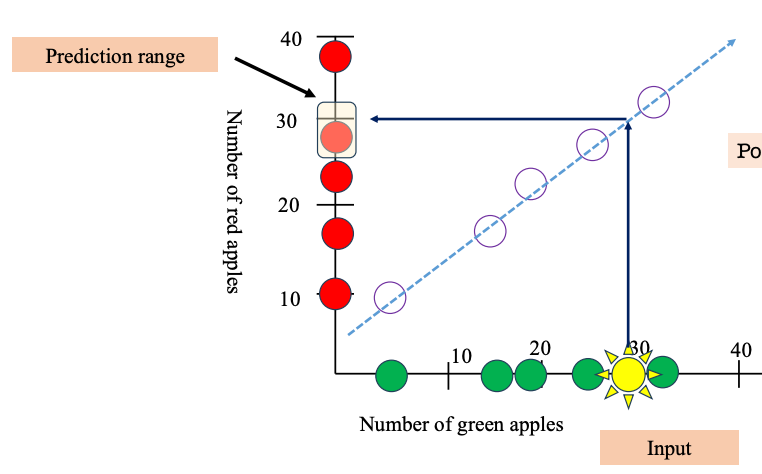image 10 10.png image 11 10.png Common Correlation Coefficients

Correlation coefficient	Type of relationship	Levels of measurement	Data distribution	Ví dụ thực tế
Pearson’s r	Linear	Two quantitative (interval or ratio) variables	Normal distribution	Điểm Toán & điểm Lý
Spearman’s rho	Non-linear	Two ordinal, interval or ratio variables	Any distribution	Xếp hạng thi & số giờ học
Point-biserial	Linear	1 dichotomous (binary) & 1 quantitative (interval/ratio)	Normal distribution	Giới tính & điểm kiểm tra
Cramér’s V (φ)	Non-linear	Two nominal variables	Any distribution	Loại đồ uống & khu vực bán
Kendall’s tau	Non-linear	Two ordinal, interval or ratio variables	Any distribution	Thứ hạng hai giám khảo

Công thức Pearson

Hệ số tương quan Pearson ký hiệu là $ρ_{x y}$ hoặc $r_{x y}$ , dùng để đo mức độ mạnh/yếu và chiều của mối liên hệ tuyến tính giữa hai biến ngẫu nhiên $x$ và y: $ρ_{x y} = \frac{cov ( X , Y )}{σ _{X} σ _{Y}}$
Biểu diễn qua tổng và trung bình: $ρ_{x y} = \frac{E [( x - μ _{x} ) ( y - μ _{y} )]}{v a r ( x ) . v a r ( y )}$ $= \frac{n \sum x _{i} y _{i} - ( \sum x _{i} ) ( \sum y _{i} )}{[ n \sum x _{i}^{2} - ( \sum x _{i} ) ^{2} ] [ n \sum y _{i}^{2} - ( \sum y _{i} ) ^{2} ]}$
Hoặc dùng sai số so với trung bình: $r_{x y} = \frac{\sum ( x _{i} - x ˉ ) ( y _{i} - y ˉ )}{\sum ( x _{i} - x ˉ ) ^{2} \sum ( y _{i} - y ˉ ) ^{2}}$

Tính chất

Giá trị luôn nằm trong đoạn $1 \leq ρ_{x y} \leq 1$

$ρ_{x y} = 1$ : Tương quan thuận hoàn hảo (cùng tăng/giảm tuyệt đối)
$ρ_{x y} = - 1$ : Tương quan nghịch hoàn hảo (một tăng, một giảm tuyệt đối)
$ρ_{x y} = 0$ : Không có tương quan tuyến tính → $∣ ρ ∣$ càng gần 1: mối liên hệ càng mạnh; càng gần 0: mối liên hệ càng yếu Không phụ thuộc vào đơn vị đo – có thể so sánh giữa mọi cặp biến:
Nếu biến đổi tuyến tính $u = a x + b, v = cy + d v = cy + d v = cy + d (a, c > 0)$ , thì:

$⁍$

Ví dụ:

Cho hai dãy số:
- $x = [7, 18, 29, 2, 10, 9, 9]$
- $y = [1, 6, 12, 8, 6, 21, 10]$
Áp dụng công thức, ta tính được:

$ρ_{x y} \approx 0.149$

Ý nghĩa: Hai biến này có tương quan thuận nhẹ (yếu).

Tạo biến mới:
- $u = 2 x - 14$
- $v = y + 2$
Dù đã biến đổi tuyến tính (thay đổi đơn vị, dịch chuyển gốc toạ độ), hệ số tương quan tính ra vẫn bằng 0.149.
- Chứng mình: $ρ_{x y} (a x, b y) = ρ_{x y} (x, y)$
  
  1. Viết lại công thức hệ số tương quan:
  
  ρxy(u,v)=E[(u−μu)(v−μv)]var(u)var(v)\rho_{xy}(u, v) = \frac{E[(u - \mu_u)(v - \mu_v)]}{\sqrt{var(u)} \sqrt{var(v)}}
  
  ρxy(u,v)=var(u)
  
  var(v)
  
  E[(u−μu)(v−μv)]
  
  Với u=axu = a xu=ax, v=byv = b yv=by:
  - μu=aμx\mu_u = a \mu_xμu=aμx
  - μv=bμy\mu_v = b \mu_yμv=bμy
  - var(u)=a2var(x)var(u) = a^2 var(x)var(u)=a2var(x)
  - var(v)=b2var(y)var(v) = b^2 var(y)var(v)=b2var(y)
  2. Thay vào công thức:
  
  ρxy(ax,by)=E[(ax−aμx)(by−bμy)]a2var(x)b2var(y)\rho_{xy}(ax, by) = \frac{E[(a x - a \mu_x)(b y - b \mu_y)]}{\sqrt{a^2 var(x)} \sqrt{b^2 var(y)}}
  
  ρxy(ax,by)=a2var(x)
  
  b2var(y)
  
  E[(ax−aμx)(by−bμy)]
  - Tử số: E[a(x−μx)⋅b(y−μy)]=ab E[(x−μx)(y−μy)]E[a(x - \mu_x) \cdot b(y - \mu_y)] = ab , E[(x - \mu_x)(y - \mu_y)]E[a(x−μx)⋅b(y−μy)]=abE[(x−μx)(y−μy)]
  - Mẫu số: a2var(x)⋅b2var(y)=∣a∣var(x)⋅∣b∣var(y)=∣ab∣var(x)var(y)\sqrt{a^2 var(x)} \cdot \sqrt{b^2 var(y)} = |a| \sqrt{var(x)} \cdot |b| \sqrt{var(y)} = |ab| \sqrt{var(x)}\sqrt{var(y)}a2var(x)⋅b2var(y)=∣a∣var(x)⋅∣b∣var(y)=∣ab∣var(x)var(y)
  3. Rút gọn:
  
  ρxy(ax,by)=ab⋅E[(x−μx)(y−μy)]∣ab∣var(x)var(y)\rho_{xy}(ax, by) = \frac{ab \cdot E[(x - \mu_x)(y - \mu_y)]}{|ab| \sqrt{var(x)}\sqrt{var(y)}}
  
  ρxy(ax,by)=∣ab∣var(x)
  
  var(y)
  
  ab⋅E[(x−μx)(y−μy)]
  
  Nếu a,b>0a, b > 0a,b>0, thì ab/∣ab∣=1ab/|ab| = 1ab/∣ab∣=1:
  
  ρxy(ax,by)=E[(x−μx)(y−μy)]var(x)var(y)=ρxy(x,y)\rho_{xy}(ax, by) = \frac{E[(x - \mu_x)(y - \mu_y)]}{\sqrt{var(x)}\sqrt{var(y)}} = \rho_{xy}(x, y)
  
  ρxy(ax,by)=var(x)
  
  var(y)
  
  E[(x−μx)(y−μy)]=ρxy(x,y)
  
  4. Tổng quát (dạng tổng quát qua tổng):
  
  Biểu thức trong hình cũng minh họa khi chuyển công thức sang dạng tổng các giá trị, các hệ số a,ba, ba,b cuối cùng đều bị rút gọn hoàn toàn khỏi tử và mẫu số.

image 12 9.png

Hệ số tương quan chính là cosine similarity trên các vector đã trừ trung bình:

Tức là các vector đã “dịch chuyển về trung tâm”.

Hệ số tương quan chính là 1 trường hợp đặc biệt của cosine similarity, nơi dữ liệu đã được chuẩn hóa bằng cách dịch chuyển gốc tọa độ về tâm (trung bình) của dữ liệu

Correlation in Python

NumPy:

import numpy as np
x = [7, 18, 29, 2, 10, 9, 9]
y = [1, 6, 12, 8, 6, 21, 10]
corr_matrix = np.corrcoef(x, y)
print(corr_matrix)
print("Pearson correlation:", corr_matrix[0, 1])

Kết quả: corr_matrix là ma trận 2x2; phần tử [0, 1] (hoặc [1, 0]) chính là hệ số tương quan Pearson giữa x và y. Scipy.stats:

from scipy.stats import pearsonr
x = [7, 18, 29, 2, 10, 9, 9]
y = [1, 6, 12, 8, 6, 21, 10]
corr, p_value = pearsonr(x, y)
print("Pearson correlation:", corr)
print("p-value:", p_value)

Trả về:

corr: hệ số tương quan ([-1, 1])
p_value: kiểm định ý nghĩa thống kê (p < 0.05 ⇒ liên hệ có ý nghĩa) Tự định nghĩa:

def pearson_corr(x, y):
    # Đảm bảo hai list có cùng độ dài
    n = len(x)
    assert n == len(y), "x và y phải có cùng số phần tử"
    # Tính trung bình
    mean_x = sum(x) / n
    mean_y = sum(y) / n
    # Tính các thành phần trong công thức
    num = sum((xi - mean_x) * (yi - mean_y) for xi, yi in zip(x, y))
    den_x = sum((xi - mean_x)**2 for xi in x)
    den_y = sum((yi - mean_y)**2 for yi in y)
    # Tính kết quả
    r = num / (den_x**0.5 * den_y**0.5)
    return r
# Ví dụ thực tế
x = [7, 18, 29, 2, 10, 9, 9]
y = [1, 6, 12, 8, 6, 21, 10]
print("Pearson correlation:", pearson_corr(x, y))

III. Applications

1. Application to Patch Matching

Patch Matching: So sánh mức độ giống nhau giữa các mảng ảnh nhỏ (patch) để tìm ảnh nào giống nhất. image 13 8.png **Giải pháp:**Dùng hệ số tương quan Pearson (ρ) giữa các vector pixel của ảnh để đo độ tương đồng.

Cơ chế

Mỗi ảnh patch chuyển thành một vector (dùng NumPy + PIL để flatten thành 1 chiều).
Tính hệ số tương quan Pearson giữa các vector này:
- ρ gần 1: Hai ảnh gần như giống hệt nhau (kể cả khi thay đổi sáng hoặc scale tuyến tính).
- ρ gần 0: Không liên hệ, ảnh rất khác.
- ρ âm: Ảnh đảo ngược tương phản. Ví dụ ở trên:
$ρ_{P_{1} P_{2}} = 0.55$ : Ảnh P2 khá giống P1
$ρ_{P_{1} P_{3}} = 0.23$ , $ρ_{P_{1} P_{4}} = 0.30$ : P3, P4 ít giống P1

⇒ P2 giống P1 hơn P3, P4
Tính chất đặc biệt:

Nếu bạn cộng/trừ một giá trị hằng số hoặc nhân scale tuyến tính vào ảnh (thay đổi sáng, độ tương phản), ρ vẫn xấp xỉ 1
- $ρ_{P_{1} P_{2}} = 0.9970$ với $P_{2} = P_{1} + 50$
- $ρ_{P_{1} P_{3}} = 0.9979$ với $P_{3} = 1.2 P_{1} + 10$

Code mẫu:

import numpy as np
from PIL import Image
# Load ảnh và chuyển về list 1 chiều
image1 = Image.open('images/img1.png')
image2 = Image.open('images/img2.png')
image1_list = np.asarray(image1).flatten().tolist()
image2_list = np.asarray(image2).flatten().tolist()
# Tính hệ số tương quan Pearson
def find_corr_x_y(x, y):
    n = len(x)
    mean_x = sum(x) / n
    mean_y = sum(y) / n
    num = sum((xi - mean_x) * (yi - mean_y) for xi, yi in zip(x, y))
    den_x = sum((xi - mean_x)**2 for xi in x)
    den_y = sum((yi - mean_y)**2 for yi in y)
    return num / (den_x**0.5 * den_y**0.5)
corr = find_corr_x_y(image1_list, image2_list)
print("Correlation:", corr)

Template matching

Tìm một hình mẫu nhỏ (template) xuất hiện ở đâu trong một ảnh lớn (image).

Ví dụ: Bạn có logo “AI VIET NAM”, muốn xác định vị trí xuất hiện của logo này trên giao diện Facebook.

Có thể ban đầu bạn sẽ nghĩ đến việc sử dụng giải thuật kiểu AD (Absolute difference) là ta lấy sự khác biệt giá trị pixel của Template lên Image. Vấn đề xuất hiện khi template bị thay đổi cường độ màu hoặc bị nhiễu.

Cơ chế giải quyết:

Trượt template trên toàn bộ ảnh lớn, tại mỗi vị trí, so sánh mức độ giống nhau (similarity) giữa vùng cắt từ ảnh lớn với template.
Ảnh trên web thường là màu (color images), nhưng xử lý template matching hiệu quả hơn khi chuyển về đen trắng (grayscale). Vì hệ số tương quan tính trên cường độ điểm ảnh, nên grayscale sẽ giúp so khớp nhanh, đơn giản và tiết kiệm tài nguyên.
Dùng hệ số tương quan (Pearson correlation) làm thước đo:
- Giá trị càng lớn (gần 1), vùng đó càng giống template.
- Vẽ bản đồ heatmap, vị trí giá trị lớn nhất (max) chính là vị trí xuất hiện của template.

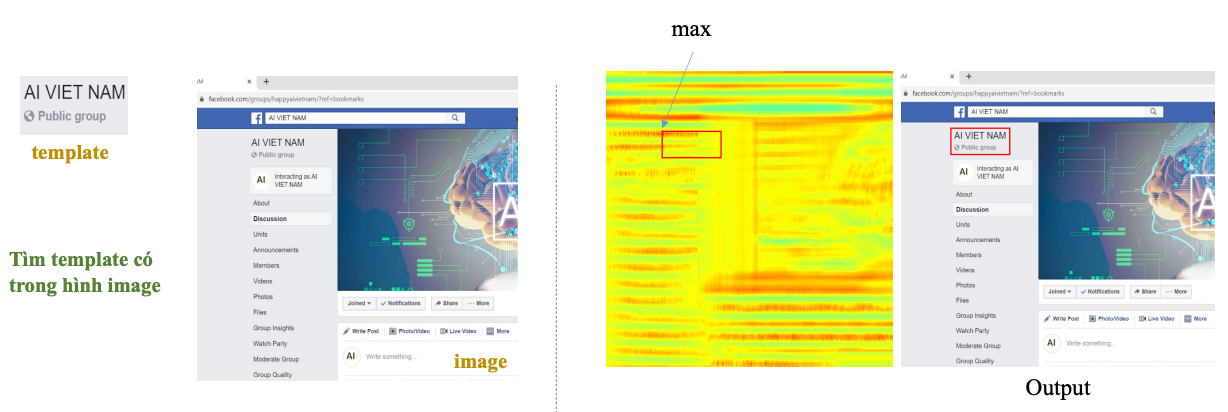
image 14 8.png

Code:

import cv2
import numpy as np
from matplotlib import pyplot as plt
\#Load image and convert to grayscale
image = cv2.imread('image.png',1)
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
\#Load template
template = cv2.imread('template.png',0)
w, h = template.shape[::-1]
\#Apply template Matching
corr_map = cv2.matchTemplate(gray, template, cv2.TM_CCOEFF_NORMED)
\#Save Correlation map
corr_map = (corr_map + 1.0) * 127.5
corr_map = corr_map.astype('uint8')
cv2.imwrite('corr_map_grayscale.png', corr_map)

image 15 8.png Giải thích code:

**template.shape** trả về kích thước của mảng ảnh (numpy array).
- Với ảnh grayscale (1 kênh), template.shape thường là (height, width)
- **[::-1]** đảo ngược thứ tự tuple này.
  - (height, width)[::-1] → (width, height)
- Sau đó gán:
  - w = width (chiều ngang template)
  - h = height (chiều dọc template)
  Tại sao phải đảo ngược (**[::-1]**)?
  - Trong OpenCV, khi vẽ hình chữ nhật (rectangle), bạn phải truyền theo thứ tự (x, y), tức là (width, height).
  - Nếu bạn lấy luôn template.shape, bạn sẽ bị ngược (bị height trước, width sau).
  - Dùng [::-1] là cách nhanh gọn để lấy đúng width, height.
cv2.matchTemplate: Hàm của OpenCV để thực hiện so khớp template trên ảnh lớn.
cv2.TM_CCOEFF_NORMED: Phương pháp tính hệ số tương quan chuẩn hóa (Normalized Cross-Correlation).
- Giá trị kết quả sẽ nằm trong khoảng [−1,1][-1, 1][−1,1]:
  - Gần 1: Vùng rất giống template.
  - Gần 0: Không liên hệ.
  - Gần -1: Ngược pha hoàn toàn (âm bản).

Ở đây xem ảnh xám hơi khó nhìn điểm matching (đóm trắng trên xám) nên ta chuyển sang ảnh màu:

An Hoai Thai's Notes

Trong bài này

M02W3.6_Statistic and Its Application

Giới thiệu

I. Basic Descriptive Statistics

1. Population Mean

2. Sample Mean

3. Degrees of Freedom

Định nghĩa gốc

Kể chuyện đồng xu

Đối với Sample Mean

Tại sao phương sai mẫu chia cho $n - 1$ ?

II. Advance Descriptive Statistics

1. Correlation

Correlation vs Regression

Correlation Between Two Variables

2. Correlation

3. Correlation vs Causation

2. Covariance - Hiệp phương sai

Review Variance

What is Covariance

Các vấn đề của Covariance

2. Correlation Coefficient

Đặc điểm

Vì sao correlation “xịn” hơn covariance?

Công thức Pearson

Tính chất

Correlation in Python

III. Applications

1. Application to Patch Matching

Cơ chế

Template matching

2. Object Detection

Biểu Đồ

Bảng Nội Dung

Liên Kết Ngược

An Hoai Thai's Notes

Trong bài này

M02W3.6_Statistic and Its Application

Giới thiệu

I. Basic Descriptive Statistics

1. Population Mean

2. Sample Mean

3. Degrees of Freedom

Định nghĩa gốc

Kể chuyện đồng xu

Đối với Sample Mean

Tại sao phương sai mẫu chia cho n−1?

II. Advance Descriptive Statistics

1. Correlation

Correlation vs Regression

Correlation Between Two Variables

2. Correlation

3. Correlation vs Causation

2. Covariance - Hiệp phương sai

Review Variance

What is Covariance

Các vấn đề của Covariance

2. Correlation Coefficient

Đặc điểm

Vì sao correlation “xịn” hơn covariance?

Công thức Pearson

Tính chất

Correlation in Python

III. Applications

1. Application to Patch Matching

Cơ chế

Template matching

2. Object Detection

Biểu Đồ

Bảng Nội Dung

Liên Kết Ngược

Tại sao phương sai mẫu chia cho $n - 1$ ?