M03W2.3_Warmup k-Nearest Neighbors (KNN)

Table of Content

---

• Tham khảo
• I. Dẫn nhập
• II. Thuật toán KNN
  • II.1.
  • II.2. Cách hoạt động

    • Bước 1: Chọn siêu tham số k

    • Bước 2: Tính khoảng cách

    • Bước 3: Tìm k láng giềng gần nhất

    • Quy trình cụ thể:

    • Ví dụ thực tế (theo tài liệu):

    • Bước 4: Ra quyết định – Dự đoán kết quả

Important

Tham khảo

KNN playground: https://aivietnam.edu.vn/space/sta-b%C3%ACnh-d%C6%B0%C6%A1ng-knn-demo-11

PCA và Kỹ Thuật Giảm Chiều Dữ Liệu

I. Dẫn nhập

Lần đầu được giới thiệu: https://apps.dtic.mil/sti/citations/AD0017838

II. Thuật toán KNN

II.1.

II.2. Cách hoạt động

Bước 1: Chọn siêu tham số k

Lưu ý:

• Khi k quá nhỏ (k = 1) → overfitting
• Khi k quá lớn (k = N) → underfitting Vậy là sao để chọn k tối ưu?
• Cross-Validation: Thử với từng giá trị k xem đâu có lỗi trung bình thấp nhất
• Rule of Thumb: chọn $k=\sqrt{N}$, N là tổng số điểm trong tập dữ liệu.
• Chọn k là số lẻ cho bài toán phân loại → tránh trường hợp hòa phiếu.

---

Bước 2: Tính khoảng cách

Khi đã chọn được tham số k (số láng giềng), bước tiếp theo cực kỳ quan trọng là xác định “ai là hàng xóm gần nhất?“. Để làm được điều này, KNN phải đo được độ gần giữa các điểm dữ liệu—chính là khoảng cách trong không gian đặc trưng

1. Chuẩn hóa dữ liệu trước khi tính khoảng cách Trong thực tế, các đặc trưng (features) của dữ liệu thường không cùng thang đo. Ví dụ:

• “Diện tích nhà” (từ 30–200 m²),
• “Số phòng ngủ” (1–5 phòng). Nếu không chuẩn hóa, các feature có giá trị lớn (ví dụ diện tích) sẽ lấn át hoàn toàn các feature nhỏ khi tính khoảng cách, dẫn đến mô hình sai lệch. Phương pháp chuẩn hóa phổ biến:

1. Min-Max Scaling (Normalization): Đưa giá trị về [0, 1] $X_{\text{scaled}}=\frac{X-X_{\text{min}}}{X_{\text{max}}-X_{\text{min}}}$ Nhược điểm: dễ bị ảnh hưởng bởi ngoại lai (outlier) b. Z-score (Standardization): Đưa dữ liệu về trung bình 0, độ lệch chuẩn $X_{\text{scaled}}=\frac{X-\mu }{\sigma }$ Trong đó μ là trung bình, σ là độ lệch chuẩn. Ưu điểm: giảm ảnh hưởng của outlier, thường được ưu tiên hơn trong mọi trường hợp Câu hỏi đào sâu:

• Khi nào thì chỉ nên dùng Min-Max?

  • Dữ liệu không có outlier hoặc rất ít outlier. Nếu toàn bộ dữ liệu nằm trong một khoảng giá trị hợp lý, Min-Max sẽ “nén” toàn bộ về [0, 1] một cách mượt mà.
  • Khi bạn cần giữ tương quan tương đối giữa các điểm (khoảng cách tỉ lệ thuận với sự khác biệt ban đầu).
  • Đặc biệt thích hợp khi các thuật toán yêu cầu dữ liệu đầu vào ở một phạm vi xác định (ví dụ: neural network với hàm kích hoạt sigmoid/tanh, hoặc các mô hình không robust với outlier).
  • Khi các feature vốn đã cùng thang đo, bạn muốn chuẩn hóa về cùng dải để dễ trực quan hóa hoặc kết hợp.

  Ví dụ:

  Dữ liệu chiều cao (150–180 cm), cân nặng (50–90 kg) trong tập luyện thể thao, không có ai vượt ngoài các ngưỡng này.

• Khi nào thì dùng Z-score?

  • Dữ liệu có outlier hoặc phân phối lệch (skewed). Z-score giúp giảm tác động của các giá trị cực đoan bằng cách quy về trung bình 0, độ lệch chuẩn 1.
  • Bạn không chắc chắn về phạm vi giá trị của dữ liệu trong tương lai, hoặc dữ liệu mới có thể mở rộng vượt xa giá trị hiện tại.
  • Phù hợp khi các thuật toán giả định dữ liệu đầu vào có phân phối chuẩn (ví dụ: Linear Regression, Logistic Regression, PCA, K-Means, v.v).
  • Khi cần so sánh các feature có đơn vị khác nhau hoặc phân phối rất khác nhau.

  Ví dụ:

  Phân tích điểm thi của học sinh trên toàn quốc, một số học sinh có điểm rất cao/thấp bất thường, hoặc dữ liệu thu thập từ nhiều nguồn (với mức độ lệch chuẩn khác nhau).

---

2. Các công thức tính khoảng cách Giả sử có hai điểm dữ liệu:

• $p=(p_1,p_2,...,p_n)$
• $q=(q_1,q_2,...,q_n)$ Các cách đo khoảng cách thường dùng: a. Khoảng cách Manhattan (L1, “đi bộ trong phố”) Tổng các khoảng cách tuyệt đối trên từng chiều: $d_{L1}(p,q)={\sum }_{i=1}^n|q_i-p_i|$ Ví dụ thực tế: Tính đường đi giữa 2 địa chỉ trong thành phố theo các trục đường thẳng (không đi xuyên tòa nhà).

---

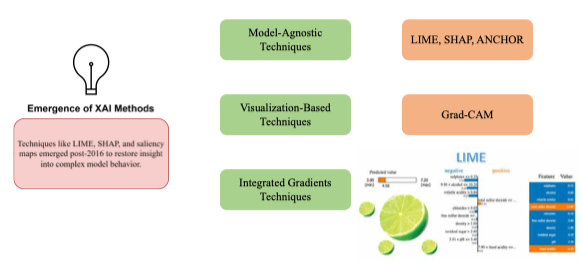
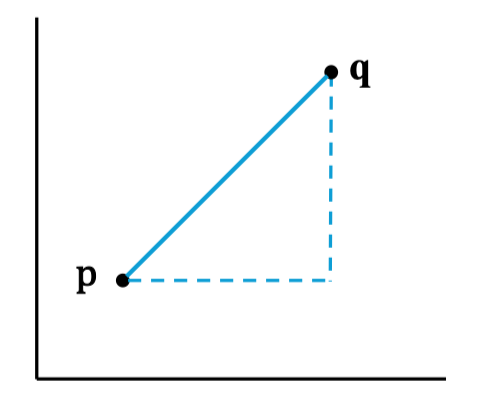
b. Khoảng cách Euclidean (L2, “đường chim bay”) Khoảng cách thẳng nhất giữa 2 điểm: $d_{L2}(p,q)=\sqrt{{\sum }_{i=1}^n(q_i-p_i{)}^2}$ Đây là công thức phổ biến nhất, thường mặc định trong KNN. Ví dụ thực tế: Tính khoảng cách giữa 2 điểm trên mặt phẳng, như dùng thước đo thẳng.

c. Khoảng cách Minkowski (Tổng quát) Tổng quát hóa L1 và L2 với tham số c: $d_c(p,q)={\left({\sum }_{i=1}^n|q_i-p_i{|}^c\right)}^{1/c}$

• Nếu c=1 → thành Manhattan.
• Nếu c=2 → thành Euclidean.
• Nếu $c\to \infty$: Khoảng cách Chebyshev (max abs diff).

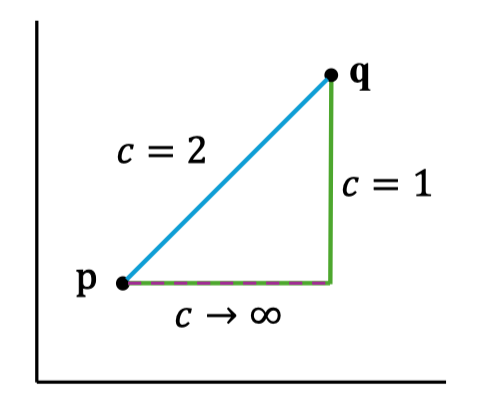Khi c tăng lên, các khác biệt lớn ở một chiều sẽ ảnh hưởng mạnh hơn tổng thể khoảng cách. Giá trị này thường ít dùng trong thực tế nhưng đôi lúc có ích nếu muốn nhấn mạnh các feature “vượt trội”. Ví dụ cụ thể (cho p=(1,2,3), q=(2,4,8)):

• $d_1=|2-1|+|4-2|+|8-3|=1+2+5=8$

• $d_2=\sqrt{(2-1{)}^2+(4-2{)}^2+(8-3{)}^2}=\sqrt{1+4+25}=\sqrt{30}\approx 5.48$

• $d_3={\left(|2-1{|}^3+|4-2{|}^3+|8-3{|}^3\right)}^{1/3}=(1^3+2^3+5^3{)}^{1/3}=(1+8+125{)}^{1/3}=134^{1/3}\approx 5.05d3=(\mid 2-1\mid 3+\mid 4-2\mid 3+\mid 8-3\mid 3)1/3=(13+23+53)1/3=(1+8+125)1/3=1341/3\approx 5.05$ Câu hỏi mở rộng:

• Nếu số chiều (feature) tăng lên rất nhiều (hàng trăm), điều gì xảy ra với khoảng cách? KNN có còn hiệu quả?

  1. Curse of Dimensionality (Lời nguyền không gian nhiều chiều)

  • Khoảng cách giữa các điểm sẽ có xu hướng trở nên “đồng đều”: Trong không gian nhiều chiều, mọi điểm gần như cách xa nhau một khoảng giống nhau. Khả năng phân biệt giữa “gần” và “xa” giảm mạnh.
  • KNN sẽ mất đi khả năng tìm hàng xóm “gần” thực sự: Các láng giềng gần nhất thực ra lại không thật sự gần, dẫn đến dự đoán kém chính xác.

  2. Độ phức tạp tính toán tăng lên

  • Tốn tài nguyên: Việc tính toán khoảng cách trên hàng trăm chiều cho mọi điểm rất tốn thời gian và bộ nhớ, đặc biệt với tập dữ liệu lớn.

  3. Nhiễu tăng cao

  • Nhiều feature không liên quan sẽ làm tăng nhiễu, khiến KNN khó học được mối liên hệ thực sự.

  Tóm lại: Khi số chiều quá lớn, KNN ít hiệu quả trừ khi bạn:

  • Giảm chiều dữ liệu (feature selection, PCA,…)
  • Loại bỏ các feature không liên quan
  • Chuẩn hóa dữ liệu thật tốt

• Nếu dữ liệu có outlier mạnh, lựa chọn chuẩn hóa và loại khoảng cách nào là tốt nhất?

  1. Chuẩn hóa

  • Nên chọn: Z-score (Standardization)
    • Giúp giảm tác động của các giá trị cực đoan (outlier).
    • Đưa tất cả các feature về trung bình 0, độ lệch chuẩn 1.
  • Không nên dùng: Min-Max nếu dữ liệu có outlier, vì outlier sẽ kéo dãn thang đo, làm phần lớn các giá trị bị “nén” về gần 0.

  2. Loại khoảng cách

  • Nên cân nhắc: Khoảng cách Manhattan (L1)

    • Ít nhạy cảm với outlier hơn so với Euclidean (L2), vì L2 sẽ bình phương sai số, làm outlier ảnh hưởng mạnh hơn.

  • Có thể thử: Một số phiên bản khoảng cách được “cắt ngọn” (clipped distance), hoặc dùng khoảng cách dựa trên thứ hạng.

    Ví dụ minh họa:

  • Nếu bạn dùng Euclidean, một điểm outlier cách xa sẽ có tác động rất lớn.

  • Nếu dùng Manhattan, sự khác biệt sẽ bớt bị phóng đại.

Bước 3: Tìm k láng giềng gần nhất

Sau khi đã chuẩn hóa dữ liệu và tính khoảng cách từ điểm dữ liệu mới ( $p_{new}$) đến từng điểm trong tập huấn luyện, việc tiếp theo là xác định k láng giềng gần nhất

Quy trình cụ thể:

1. Sắp xếp các điểm trong tập huấn luyện theo thứ tự khoảng cách tăng dần so với $p_{new}$
2. Chọn ra k điểm có khoảng cách nhỏ nhất. Đây chính là “hàng xóm” sẽ cùng tham gia “bầu chọn” quyết định kết quả cho $p_{new}$ Công thức sắp xếp: Gọi $d(p_{new},p_i)$ là khoảng cách từ $p_{new}$ đến điểm $p_i$ trong tập huấn luyện. Ta sắp xếp tất cả các $p_i$ theo thứ tự tăng dần của $d(p_{new},p_i)$, rồi chọn $k$ điểm đầu tiên.

Ví dụ thực tế (theo tài liệu):

Giả sử bạn đã tính được khoảng cách từ $p_{new}=(4,7)$ tới từng sinh viên: Nếu k = 3, ba láng giềng gần nhất là $p_2,p_5,p_3$ Lưu ý quan trọng:

• Nếu có nhiều điểm cùng khoảng cách, có thể ưu tiên chọn điểm xuất hiện sớm hơn hoặc tăng k lên.
• Khi dữ liệu lớn, có thể dùng các cấu trúc dữ liệu như KD-Tree, Ball-Tree để tăng tốc tìm kiếm láng giềng.

---

Bước 4: Ra quyết định – Dự đoán kết quả

Đây là bước mà thuật toán KNN đưa ra dự đoán dựa trên “ý kiến” của các láng giềng vừa tìm được. Cách ra quyết định sẽ phụ thuộc vào dạng bài toán: A. Bài toán Phân loại (Classification) Nguyên tắc:

• Biểu quyết theo số đông (Majority Vote):

  • Lớp nào xuất hiện nhiều nhất trong k láng giềng thì sẽ được chọn làm nhãn cho $p_{new}$.
  • Ví dụ:
    • Với $k=3$ , ba láng giềng có nhãn: “Trượt”, “Đậu”, “Đậu”.
    • “Đậu” xuất hiện 2 lần → Kết quả: Dự đoán là “Đậu”.

• Cải tiến: Có thể dùng trọng số cho từng láng giềng (láng giềng càng gần càng được “ưu tiên” hơn), ví dụ:

  $w_i=\frac{1}{d(p_{new},p_i)}$

  Mỗi phiếu bầu được nhân với trọng số, tổng hợp lại để quyết định.

  Ví dụ:

  Bạn cần dự đoán kết quả học tập của một sinh viên mới $p_{new}$ dựa trên 3 láng giềng gần nhất, với các thông tin:

  Điểm dữ liệu	Khoảng cách đến $p_{new}$	Nhãn (Phân loại)	Điểm thi (Hồi quy)
  $p_2$	1.00	Trượt	5.5
  $p_5$	1.00	Đậu	7.0
  $p_3$	1.41	Đậu	7.5

  Tính trọng số cho từng láng giềng:

  Trọng số $w_i=\frac{1}{d(p_{new},p_i)}$

  • $w_2=\frac{1}{1.00}=1.0$
  • $w_5=\frac{1}{1.00}=1.0$
  • $w_3=\frac{1}{1.41}\approx 0.709$

  Phân loại (Classification): Biểu quyết theo trọng số

  Mỗi nhãn sẽ được cộng tổng trọng số từ các láng giềng có nhãn đó:

  • Trượt:
    • $p_2\to 1.0$
    • Tổng: 1.0
  • Đậu:
    • $p_5\to 1.0$
    • $p_3\to 0.709$
    • Tổng: 1.0 + 0.709 = 1.709

  Kết quả:

  • Trọng số tổng cho “Đậu” > “Trượt”
  • Dự đoán: Đậu

  ---

  ---

---