M03W2.4_K-Mean

Table of Content

---

• Tham khảo
• I. K-Means
  • II.1. Procedure
  • I.2. K-Means Algorithm
  • I.3. Công thức (Formulae)
    • Giải thích công thức mục tiêu của K-Means
    • Giải thích Assignment step và Update step trong K-Means
• II. Tabular Data
  • II.1. Simple Example
    • Bước 1: Khởi tạo K centroids (randomly)
    • Bước 2: Tính khoảng cách đến từng centroid
    • Bước 3: Gán nhãn cho từng điểm dữ liệu
    • Bước 4: Cập nhật lại centroids
    • Vòng lặp 2 – Bước 2: Tính khoảng cách đến từng centroid
    • Vòng lặp 2 – Bước 3: Gán nhãn cho từng điểm dữ liệu
    • Vòng lặp 2 – Bước 4: Cập nhật lại centroids
  • II.2. Implementation using Numpy
    • Chuẩn bị dữ liệu và centroids
    • Tính khoảng cách bằng broadcasting
    • Gán nhãn bằng np.argmin
    • Cập nhật centroid bằng NumPy (từ nhãn)
    • Kiểm tra điều kiện dừng với np.all
    • Tính WCSS (Within-Cluster Sum of Squares) bằng NumPy
  • II. 3. Features = 2, Clusters = 3

    • Dataset

    • Targets

    • Step 1 — Init Centroids by random pickup

    • Step 2 — Assign labels

    • Step 3 — Update Centroids (vòng 1)

    • Repeat Step 2 — Calculate distance (vòng 2)

Important

Tham khảo

I. K-Means

Phần này giới thiệu quy trình (procedure) cơ bản của thuật toán K-Means, mô tả các bước từ khởi tạo đến điều kiện dừng.

II.1. Procedure

Các bước thực hiện thuật toán K-Means:

1. Khởi tạo giá trị K – Xác định số cụm cần phân loại.
2. Chọn ngẫu nhiên K trọng tâm (centroids) ban đầu.
3. Gán từng điểm dữ liệu vào trọng tâm gần nhất.
4. Tính toán lại vị trí trọng tâm của từng cụm dựa trên các điểm dữ liệu trong cụm.
5. Kiểm tra hội tụ: Nếu chưa hội tụ, quay lại bước 3; nếu hội tụ, dừng thuật toán.

💡 Tip: Hội tụ xảy ra khi vị trí các trọng tâm không thay đổi hoặc thay đổi rất nhỏ qua các vòng lặp, hoặc khi đạt số vòng lặp tối đa đã định.

• Câu hỏi gợi mở
  1. Có những chiến lược nào để chọn trọng tâm ban đầu ngoài cách chọn ngẫu nhiên?
  2. Nếu dữ liệu chứa nhiều nhiễu (noise), kết quả hội tụ sẽ bị ảnh hưởng như thế nào?
  3. Điều kiện dừng nào ngoài hội tụ có thể được áp dụng cho K-Means?

I.2. K-Means Algorithm

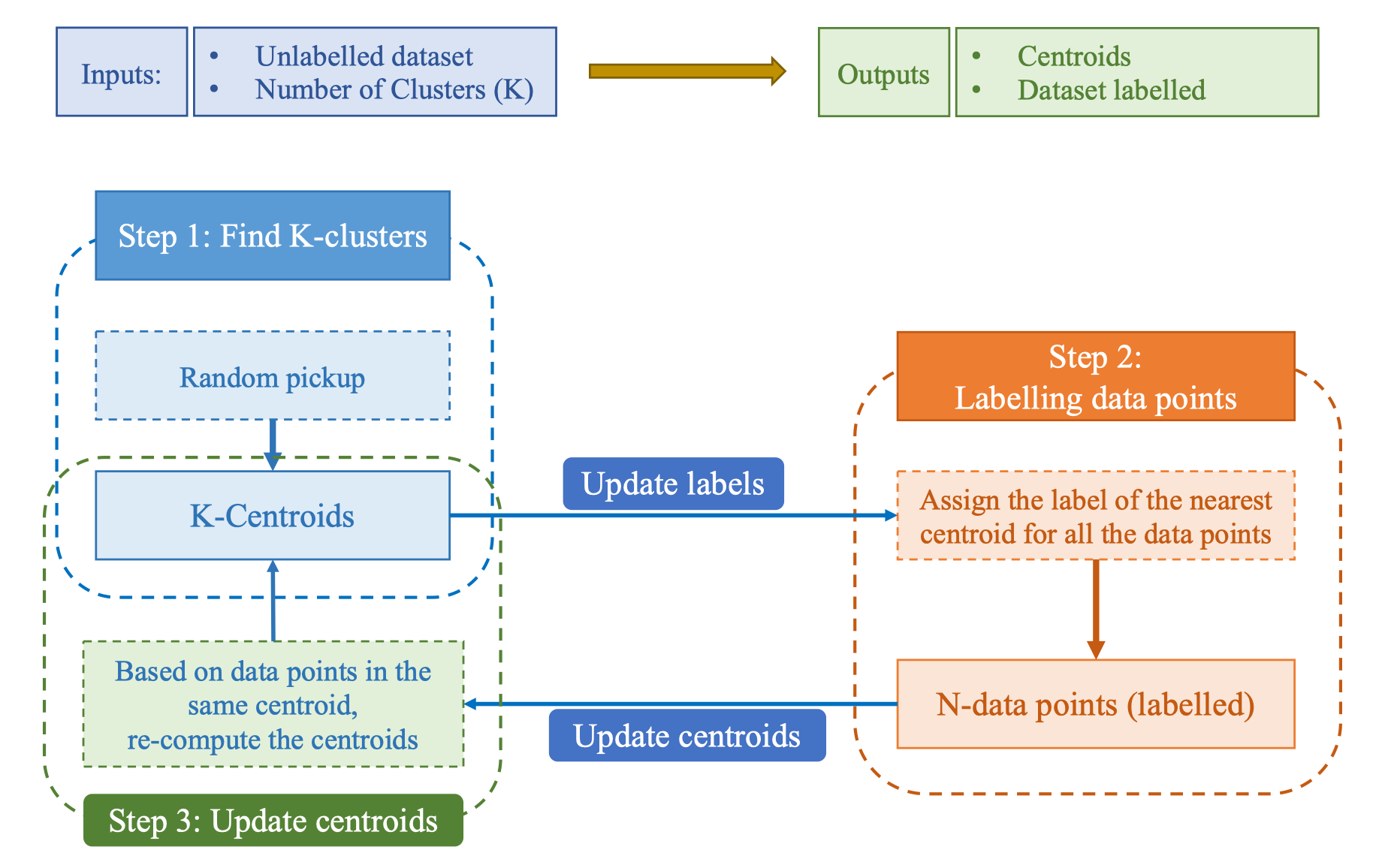Inputs:

• Unlabelled dataset – Tập dữ liệu chưa gán nhãn.
• Number of clusters (K) – Số cụm mong muốn. Outputs:
• Centroids – Tọa độ của K trọng tâm.
• Dataset labelled – Tập dữ liệu đã gán nhãn cụm. Các bước thuật toán:

1. Step 1 – Find K-clusters
   • Chọn ngẫu nhiên K trọng tâm ban đầu (Random pickup).
   • Dựa trên các điểm dữ liệu thuộc cùng một trọng tâm, tính lại vị trí trọng tâm mới.
2. Step 2 – Labelling data points
   • Gán nhãn cụm của trọng tâm gần nhất cho từng điểm dữ liệu.
3. Step 3 – Update centroids
   • Dựa trên nhãn vừa gán, cập nhật lại vị trí các trọng tâm. Quá trình lặp lại Update labels và Update centroids cho đến khi hội tụ. [Hình: Sơ đồ thuật toán K-Means với các bước tìm cụm, gán nhãn và cập nhật trọng tâm]

💡 Tip: Việc chọn trọng tâm ban đầu ảnh hưởng lớn đến kết quả phân cụm; phương pháp K-Means++ giúp khởi tạo tốt hơn và giảm rủi ro hội tụ vào nghiệm cục bộ.

• Câu hỏi gợi mở
  1. Trong thực tế, nên dừng K-Means dựa trên tiêu chí hội tụ nào?
  2. Nếu dữ liệu ban đầu không đồng nhất về thang đo, điều gì sẽ xảy ra với quá trình gán cụm?
  3. K-Means++ khác gì so với K-Means cơ bản trong bước chọn trọng tâm ban đầu?

---

I.3. Công thức (Formulae)

Cho tập dữ liệu:

• $(x_1,x_2,...,x_n)$ với $(x_i\in {\mathbb{R}}^d)$
• Tập trọng tâm ban đầu gồm $k$ phần tử: $c_0^{(1)},c_1^{(1)},...$
• Tập cụm $S=(S_0,S_1,...)$gồm $k$ cụm. Mục tiêu tối ưu: $\underset{S}{\mathrm{argmin}}{\sum }_{i=0}^{k-1}{\sum }_{x\in S_i}\Vert x-c_i{\Vert }^2$ Chuẩn (Norm): $\Vert \vec{u}\Vert =\sqrt{u_1^2+\cdots +u_d^2}$ Chuẩn bình phương (Squared norm): $\Vert \vec{u}{\Vert }^2=u_1^2+\cdots +u_d^2$

Giải thích công thức mục tiêu của K-Means

Ý nghĩa:

• $S$: Tập các cụm (clusters) S₀, S₁, …, Sₖ₋₁.
• $c_i$: Trọng tâm (centroid) của cụm Sᵢ.
• $x$: Một điểm dữ liệu trong tập dữ liệu ban đầu.
• $\Vert x-c_i{\Vert }^2$: Bình phương khoảng cách Euclidean giữa điểm dữ liệu x và trọng tâm cᵢ. Diễn giải:
• Vòng lặp ${\sum }_{i=0}^{k-1}$: Duyệt qua tất cả các cụm.
• Vòng lặp ${\sum }_{x\in S_i}$: Duyệt qua tất cả các điểm dữ liệu thuộc cụm Sᵢ.
• Mục tiêu: Tìm tập phân cụm S sao cho tổng bình phương khoảng cách từ mỗi điểm dữ liệu đến trọng tâm cụm của nó là nhỏ nhất (minimize).
• argmin: Trả về cấu hình phân cụm S tối ưu đạt giá trị nhỏ nhất cho hàm mục tiêu. Hiểu đơn giản:

Thuật toán K-Means cố gắng nhóm các điểm dữ liệu lại sao cho các điểm trong cùng một cụm càng gần trọng tâm của cụm đó càng tốt, và tổng khoảng cách bình phương của tất cả các điểm đến trọng tâm là nhỏ nhất.

Giải thích Assignment step và Update step trong K-Means

Assignment step: $S_i^{(t)}=\{x_p:\Vert x_p-c_i^{(t)}{\Vert }^2\le \Vert x_p-c_j^{(t)}{\Vert }^2\forall j,0\le j<k\}$

• $S_i^{(t)}$: Tập các điểm dữ liệu thuộc cụm i ở vòng lặp thứ t.
• $x_p$: Một điểm dữ liệu trong tập dữ liệu.
• $c_i^{(t)}$: Tọa độ trọng tâm của cụm i ở vòng lặp thứ t.
• $\Vert x_p-c_i^{(t)}{\Vert }^2$: Bình phương khoảng cách Euclidean từ điểm dữ liệu xₚ đến trọng tâm cᵢ^(t). Ý nghĩa: Mỗi điểm dữ liệu xₚ được gán vào cụm có trọng tâm gần nó nhất (khoảng cách bình phương nhỏ nhất so với tất cả các trọng tâm khác).

---

Update step: $c_i^{(t+1)}=\frac{1}{|S_i^{(t)}|}{\sum }_{x\in S_i^{(t)}}x$

• $c_i^{(t+1)}$: Tọa độ trọng tâm của cụm i ở vòng lặp thứ t+1.
• $|S_i^{(}t)|$: Số lượng điểm dữ liệu trong cụm i ở vòng lặp thứ t.
• ${\sum }_{x\in S_i^{(t)}}x$: Tổng các tọa độ điểm dữ liệu thuộc cụm i ở vòng lặp thứ t. Ý nghĩa: Trọng tâm mới được tính bằng trung bình cộng của tất cả các điểm dữ liệu trong cụm. Sau khi tính trọng tâm mới cho tất cả các cụm, thuật toán quay lại bước Assignment step để gán lại các điểm.

💡 Tip: Việc cập nhật trọng tâm liên tục giúp các cụm trở nên ổn định hơn sau mỗi vòng lặp và tiến dần đến hội tụ.

---

II. Tabular Data

II.1. Simple Example

Bước 1: Khởi tạo K centroids (randomly)

Cho bảng dữ liệu ban đầu:

Index	Length
0	1.4
1	1.0
2	1.5
3	3.1
4	3.8
5	4.1
![[image 3 25.png	image 3 25.png]]
Giả sử ta chọn K = 2, các trọng tâm ban đầu được chọn ngẫu nhiên như sau:

• C₀ = 1.4
• C₁ = 1.0 Bảng gán ban đầu: |Index|Length|Centroid| |---|---|---| |1|1.4|centroid 0| |2|1.0|centroid 1| |3|1.5|-| |4|3.1|-| |5|3.7|-| |6|4.1|-|

💡 Tip: Việc chọn trọng tâm ban đầu ảnh hưởng đến kết quả phân cụm cuối cùng. Nếu chọn không tốt, thuật toán có thể hội tụ vào nghiệm cục bộ.

• Câu hỏi gợi mở
  1. Ngoài chọn ngẫu nhiên, có những chiến lược nào khác để khởi tạo centroid?
  2. Nếu hai centroid ban đầu quá gần nhau, điều gì sẽ xảy ra với quá trình phân cụm?
  3. K-Means++ giúp cải thiện bước khởi tạo như thế nào?

Bước 2: Tính khoảng cách đến từng centroid

Với K = 2, các centroid ban đầu:

• C₀ = 1.4
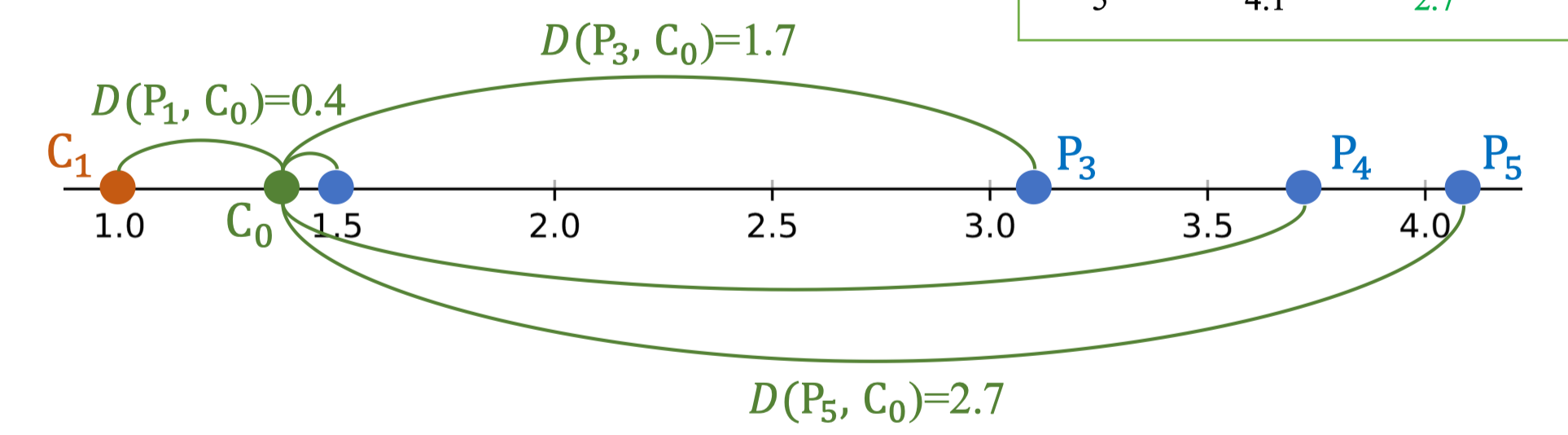
• C₁ = 1.0 Ta tính khoảng cách Euclidean từ từng điểm dữ liệu đến mỗi centroid. Công thức khoảng cách Euclidean 1 chiều: $D(P,C)=|{\text{Length}}_P-{\text{Length}}_C|$ Bảng kết quả: |Index|Length|Distance to C₀|Distance to C₁|Centroid| |---|---|---|---|---| |0|1.4|0.0|0.4|0| |1|1.0|0.4|0.0|1| |2|1.5|0.1|0.5|-| |3|3.1|1.7|2.1|-| |4|3.8|2.4|2.8|-| |5|4.1|2.7|3.1|-| Ví dụ minh họa:
• D(P₁, C₀) = 0.4
• D(P₃, C₀) = 1.7
• D(P₅, C₀) = 2.7

💡 Tip: Khi dữ liệu chỉ có một thuộc tính số, khoảng cách Euclidean là giá trị tuyệt đối của hiệu giữa hai số. Trong trường hợp nhiều chiều, cần tính theo công thức căn bậc hai tổng bình phương chênh lệch từng thuộc tính.

• Câu hỏi gợi mở
  1. Tại sao K-Means sử dụng khoảng cách Euclidean mặc định?
  2. Nếu dữ liệu có thuộc tính dạng phân loại (categorical), khoảng cách sẽ được tính thế nào?
  3. Trong trường hợp nhiều chiều, việc chuẩn hóa dữ liệu ảnh hưởng ra sao đến kết quả tính khoảng cách?

Bước 3: Gán nhãn cho từng điểm dữ liệu

Với K = 2, các centroid ban đầu:

• C₀ = 1.4
• C₁ = 1.0 Nguyên tắc gán nhãn: Mỗi điểm dữ liệu được gán vào cụm có khoảng cách tới centroid nhỏ nhất. Bảng kết quả sau khi gán: |Index|Length|Distance to C₀|Distance to C₁|Centroid|Label| |---|---|---|---|---|---| |0|1.4|0.0|0.4|0|0| |1|1.0|0.4|0.0|1|1| |2|1.5|0.1|0.5|-|0| |3|3.1|1.7|2.1|-|0| |4|3.8|2.4|2.8|-|0| |5|4.1|2.7|3.1|-|0| Ví dụ minh họa:
• P₄:
  • D(P₄, C₀) = 2.4
  • D(P₄, C₁) = 2.8
    → P₄ được gán vào cụm C₀ vì khoảng cách tới C₀ nhỏ hơn.
• P₃:
  • D(P₃, C₀) = 1.7
  • D(P₃, C₁) = 2.1
    → P₃ cũng thuộc C₀.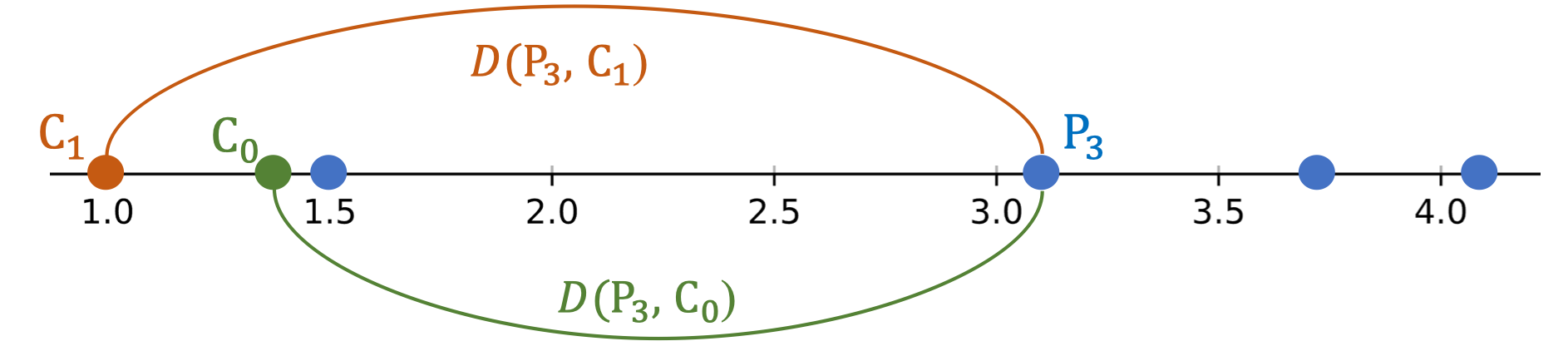

💡 Tip: Sau bước gán nhãn, tất cả các điểm trong cùng một cụm sẽ có cùng nhãn, và quá trình sẽ tiếp tục với bước cập nhật centroid.

• Câu hỏi gợi mở
  1. Điều gì sẽ xảy ra nếu hai khoảng cách bằng nhau khi gán cụm?
  2. Nếu một cụm không có điểm nào được gán, cần xử lý thế nào?
  3. Có thể dùng tiêu chí khác ngoài khoảng cách để gán cụm không?

Bước 4: Cập nhật lại centroids

Sau khi gán nhãn cho tất cả các điểm dữ liệu, ta tiến hành cập nhật centroid của mỗi cụm bằng cách lấy trung bình cộng giá trị các điểm trong cụm đó. Công thức: $c_i^{(t+1)}=\frac{1}{|S_i^{(t)}|}{\sum }_{x\in S_i^{(t)}}x$ Với dữ liệu hiện tại:

• C₀: $C_0=\frac{1.4+1.5+3.1+3.8+4.1}{5}=2.78$
• C₁: $C_1=1.0$
  (vì chỉ có 1 điểm duy nhất trong cụm này) Bảng sau khi cập nhật centroid: |Index|Length|Distance to C₀|Distance to C₁|Centroid|Label| |---|---|---|---|---|---| |0|1.4|0.0|0.4|0|0| |1|1.0|0.4|0.0|1|1| |2|1.5|0.1|0.5|-|0| |3|3.1|1.7|2.1|-|0| |4|3.8|2.4|2.8|-|0| |5|4.1|2.7|3.1|-|0|

💡 Tip: Nếu một cụm có rất ít điểm, vị trí centroid mới có thể dịch chuyển mạnh so với vòng lặp trước. Điều này ảnh hưởng lớn đến việc phân cụm ở các vòng lặp tiếp theo.

• Câu hỏi gợi mở
  1. Tại sao sau khi cập nhật, một số centroid có thể không thay đổi vị trí?
  2. Điều gì sẽ xảy ra nếu một cụm không có điểm dữ liệu nào?
  3. Khi nào thì nên dừng việc cập nhật centroid trong K-Means?

Vòng lặp 2 – Bước 2: Tính khoảng cách đến từng centroid

Sau khi cập nhật centroid ở vòng lặp 1:

• C₀ = 2.78
• C₁ = 1.0 Ta tính lại khoảng cách từ mỗi điểm dữ liệu đến các centroid mới. |Index|Length|Distance to C₀|Distance to C₁|Label| |---|---|---|---|---| |0|1.4|1.38|0.4|-| |1|1.0|1.78|0.0|-| |2|1.5|1.28|0.5|-| |3|3.1|0.32|2.1|-| |4|3.8|1.02|2.8|-| |5|4.1|1.32|3.1|-| Ví dụ minh họa:
• P₀: D(P₀, C₀) = 1.38, D(P₀, C₁) = 0.4 → gần C₁ hơn.
• P₄: D(P₄, C₀) = 1.02, D(P₄, C₁) = 2.8 → gần C₀ hơn.

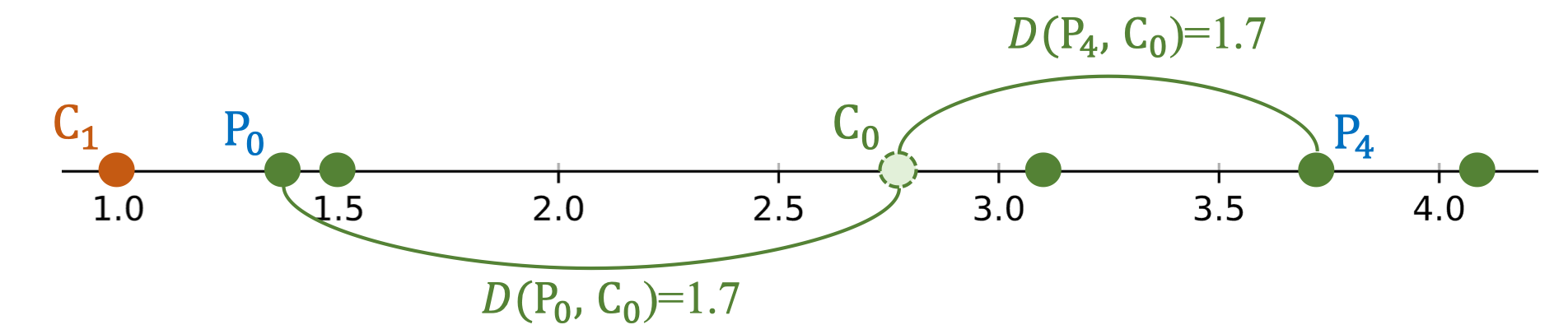
💡 Tip: Khi centroid di chuyển, nhiều điểm dữ liệu có thể thay đổi cụm gán, dẫn đến sự thay đổi đáng kể trong phân cụm ở vòng lặp tiếp theo.

• Câu hỏi gợi mở
  1. Tại sao khoảng cách của một số điểm lại giảm so với vòng lặp trước?
  2. Có thể xảy ra trường hợp centroid mới nằm ngoài phạm vi dữ liệu ban đầu không?
  3. Khi nào thì thuật toán sẽ không còn thay đổi nhãn của các điểm dữ liệu?

Vòng lặp 2 – Bước 3: Gán nhãn cho từng điểm dữ liệu

Sau khi tính lại khoảng cách ở vòng lặp 2, ta gán nhãn dựa trên nguyên tắc: Điểm dữ liệu được gán vào cụm có khoảng cách nhỏ nhất tới centroid.

Index	Length	Distance to C₀	Distance to C₁	Label
0	1.4	1.38	0.4	1
1	1.0	1.78	0.0	1
2	1.5	1.28	0.5	1
3	3.1	0.32	2.1	0
4	3.8	1.02	2.8	0
5	4.1	1.32	3.1	0
Kết quả:

• Nhóm C₁: P₀, P₁, P₂ (các điểm gần C₁ hơn)
• Nhóm C₀: P₃, P₄, P₅ (các điểm gần C₀ hơn)

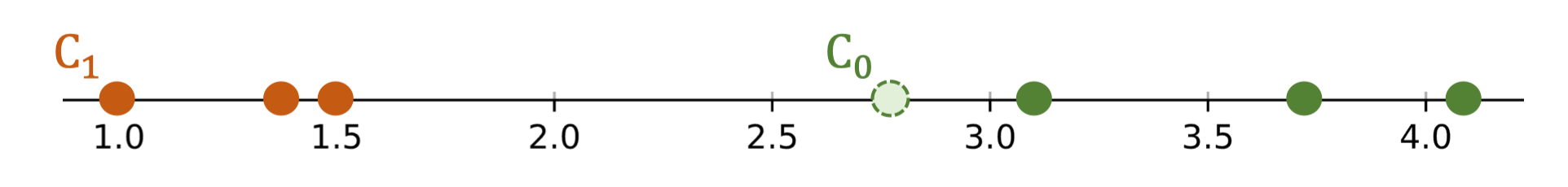
💡 Tip: Khi centroid di chuyển nhiều giữa các vòng lặp, có thể dẫn đến việc thay đổi phân cụm đáng kể, đặc biệt khi các cụm ban đầu chưa ổn định.

• Câu hỏi gợi mở
  1. Nếu tất cả các nhãn cụm không thay đổi so với vòng lặp trước, điều gì sẽ xảy ra?
  2. Có thể xảy ra trường hợp một cụm trống (không có điểm dữ liệu) sau khi gán lại không?
  3. Việc gán lại cụm nhiều lần có thể dẫn đến tình trạng lặp vô hạn không?

Vòng lặp 2 – Bước 4: Cập nhật lại centroids

Sau khi gán nhãn mới ở vòng lặp 2, ta tính lại vị trí centroid cho từng cụm.

• C₀ (gồm các điểm: 3.1, 3.8, 4.1): $C_0=\frac{3.1+3.8+4.1}{3}=3.67$
• C₁ (gồm các điểm: 1.4, 1.0, 1.5): $C_1=\frac{1.4+1.0+1.5}{3}=1.3$ Bảng dữ liệu sau khi xác định lại cụm và tính centroid: |Index|Length|Distance to C₀|Distance to C₁|Label| |---|---|---|---|---| |0|1.4|1.38|0.4|1| |1|1.0|1.78|0.0|1| |2|1.5|1.28|0.5|1| |3|3.1|0.32|2.1|0| |4|3.8|1.02|2.8|0| |5|4.1|1.32|3.1|0|

💡 Tip: Khi centroid dịch chuyển ít giữa các vòng lặp, thuật toán đang tiến gần đến trạng thái hội tụ. Nếu sau khi cập nhật, nhãn cụm không thay đổi, K-Means sẽ dừng.

• Câu hỏi gợi mở
  1. Tại sao C₀ dịch chuyển về phía các giá trị lớn hơn?
  2. Nếu C₁ và C₀ tiến lại gần nhau, điều gì sẽ xảy ra với phân cụm?
  3. Có nên giới hạn số vòng lặp để tránh tính toán quá lâu khi dữ liệu rất lớn?

---

II.2. Implementation using Numpy

Mục tiêu: Minh họa cách tính khoảng cách đến các centroid và gán nhãn theo cách vector hóa bằng NumPy (không dùng vòng lặp thủ công).

Chuẩn bị dữ liệu và centroids

Dữ liệu 1 chiều:

• X = [1.4, 1.0, 1.5, 3.1, 3.8, 4.1]
• C = [1.4, 1.0] với:
  • C₀ = 1.4
  • C₁ = 1.0

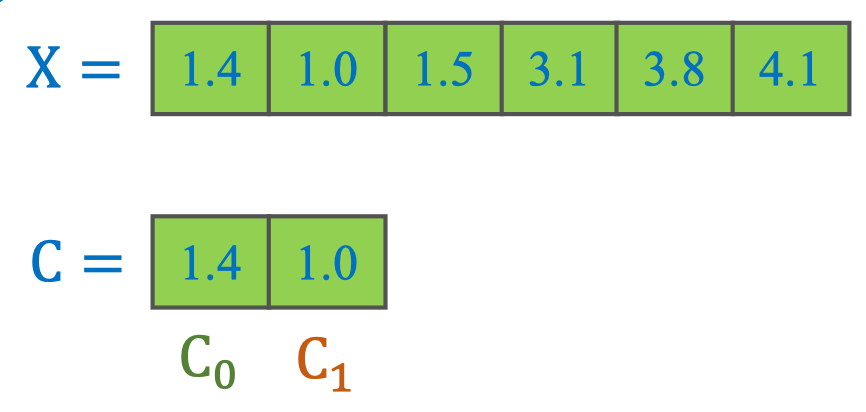
import numpy as np
X = np.array([1.4, 1.0, 1.5, 3.1, 3.8, 4.1], dtype=float)
C = np.array([1.4, 1.0], dtype=float)  # C0, C1

• Câu hỏi gợi mở
  1. Khi chuyển sang dữ liệu nhiều chiều, cấu trúc X và C nên biểu diễn thế nào?
  2. Chúng ta cần ràng buộc gì để đảm bảo C không rỗng ở các vòng lặp?

Tính khoảng cách bằng broadcasting

Với dữ liệu 1 chiều X và các centroid C₀, C₁, ta có thể tính khoảng cách tới từng centroid bằng NumPy mà không cần vòng lặp.

# Tính khoảng cách tuyệt đối (Euclidean 1D)
d_to_c0 = np.abs(X - C[0])
d_to_c1 = np.abs(X - C[1])
print(d_to_c0)  # [0.  0.4 0.1 1.7 2.4 2.7]
print(d_to_c1)  # [0.4 0.  0.5 2.1 2.8 3.1]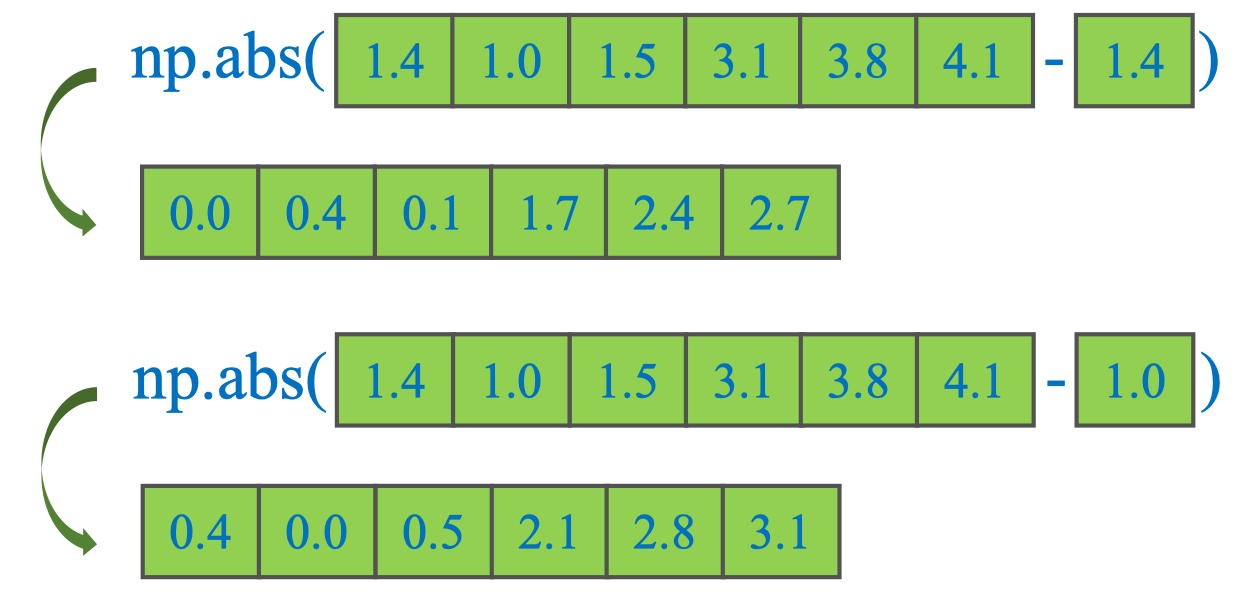

Chú ý: Khi làm việc với NumPy, để tính khoảng cách giữa toàn bộ điểm dữ liệu X và tất cả các centroid C trong một phép toán, cần chú ý tới shape của mảng. Nếu viết:

np.abs(X - C)

sẽ báo lỗi ValueError vì NumPy không thể broadcast hai mảng (6,) và (2,) trực tiếp. Cách khắc phục: Thêm một chiều cho C để có shape (2,1) hoặc reshape X thành (1,6) để NumPy broadcast đúng.

# Reshape C thành cột (2,1)
C = C.reshape(-1, 1)  # shape (2,1)
# Broadcasting: (2,1) - (6,) -> (2,6)
distances = np.abs(X - C)
print(distances)
# [[0.  0.4 0.1 1.7 2.4 2.7]
#  [0.4 0.  0.5 2.1 2.8 3.1]]

Ý nghĩa kết quả:

• Hàng 0: khoảng cách từ tất cả các điểm tới C₀
• Hàng 1: khoảng cách từ tất cả các điểm tới C₁

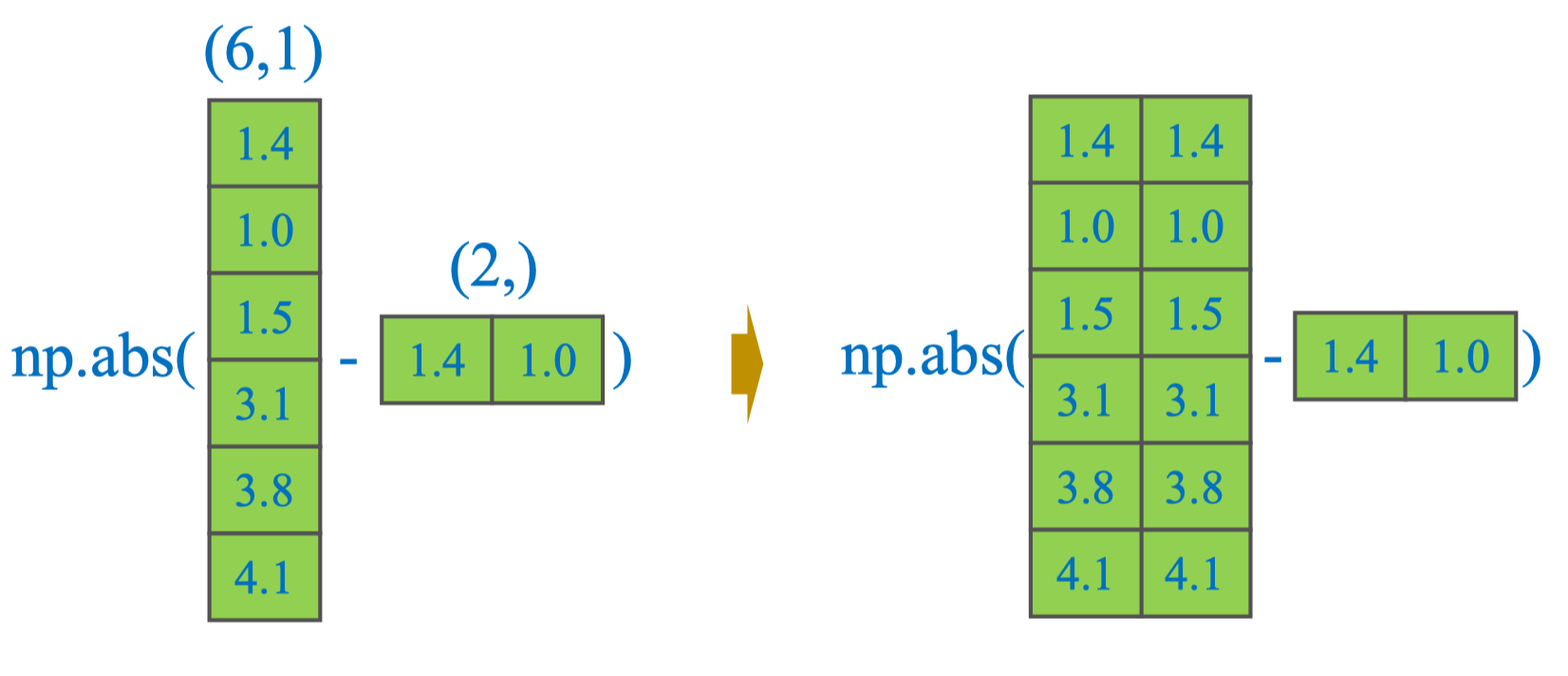
Tip: Cách này cho ma trận khoảng cách có shape (n, K) (thuận tiện để dùng labels = D.argmin(axis=1) cho bước gán nhãn). Cách trước đó (reshape C → (K,1)) tạo ma trận (K, n) — cả hai đều đúng, tuỳ bạn muốn argmin theo trục nào.

• Câu hỏi gợi mở
  1. Có thể dùng np.newaxis thay cho reshape(-1, 1) để thêm chiều không?
  2. Khi dữ liệu nhiều chiều, cách tính khoảng cách Euclidean bằng broadcasting thay đổi thế nào?
  3. Làm sao tối ưu bộ nhớ khi ma trận khoảng cách quá lớn?

Gán nhãn bằng np.argmin

Từ ma trận khoảng cách D có shape (n, K) (mỗi hàng là một điểm, mỗi cột là một centroid), ta gán nhãn cho từng điểm bằng cách chọn cột có khoảng cách nhỏ nhất trên mỗi hàng.

import numpy as np
X = np.array([1.4, 1.0, 1.5, 3.1, 3.8, 4.1])# (n,)
C = np.array([1.4, 1.0])                    # (K,)
D = np.abs(X.reshape(-1, 1) - C)            # (n, K)
labels = D.argmin(axis=1)                   # (n,)
print(D)
print(labels)  # -> [0, 1, 0, 0, 0, 0]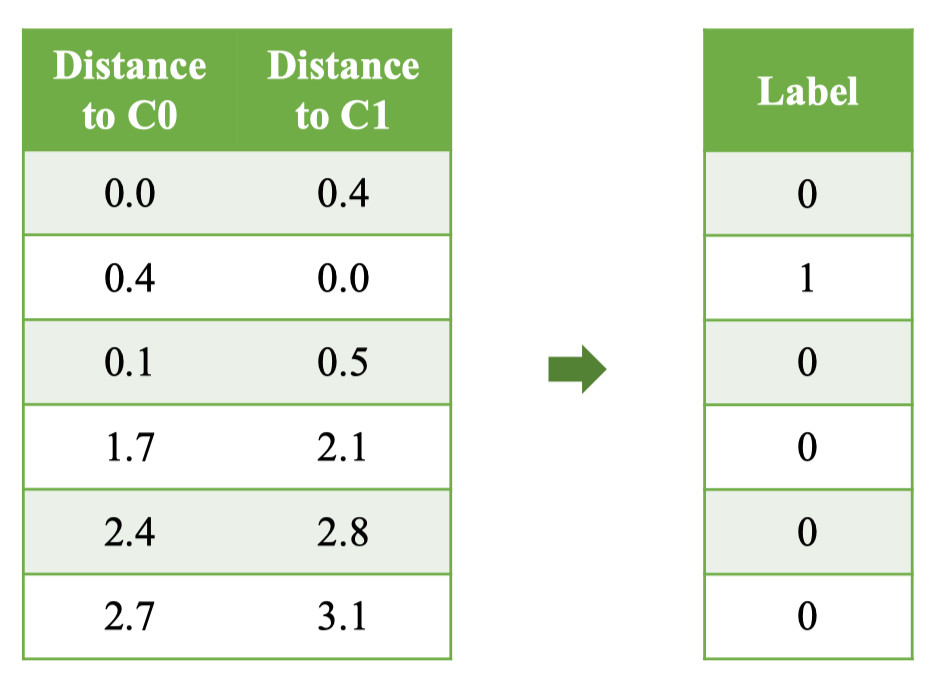

Ngoài ra, có thể kiểm tra “tâm gần nhất” theo cột bằng:

closest_rows_each_centroid = D.argmin(axis=0)  # (K,)
# -> [0, 1]  # hàng gần nhất với C0 và C1

💡 Tip: np.argmin trả về vị trí nhỏ nhất đầu tiên nếu có hòa. Khi bạn xây dựng quy tắc “bẻ hòa”, có thể cộng một nhiễu nhỏ theo seed cố định để ổn định kết quả, hoặc tự viết hàm chọn theo tie-break mong muốn.

• Câu hỏi gợi mở
  1. Nếu D có shape (K, n) (mỗi hàng là centroid), bạn sẽ dùng argmin theo trục nào để vẫn nhận về nhãn theo thứ tự điểm?
  2. Làm sao chuyển labels sang one-hot kích thước (n, K) một cách vector hóa?
  3. Bạn sẽ kiểm thử tính đúng đắn của labels như thế nào (ví dụ: so khớp với khoảng cách tối thiểu từng hàng)?

Cập nhật centroid bằng NumPy (từ nhãn)

Sau khi đã có nhãn cho từng điểm (labels) và dữ liệu X, ta cập nhật centroid bằng trung bình các điểm thuộc từng cụm. Cách 1 — boolean indexing + mean:

import numpy as np
X = np.array([1.4, 1.0, 1.5, 3.1, 3.8, 4.1], dtype=float)
L = np.array([0, 1, 0, 0, 0, 0], dtype=int)
k = 2
C_new = np.array([X[L == i].mean() for i in range(k)])
print(C_new)  # [2.78 1.  ]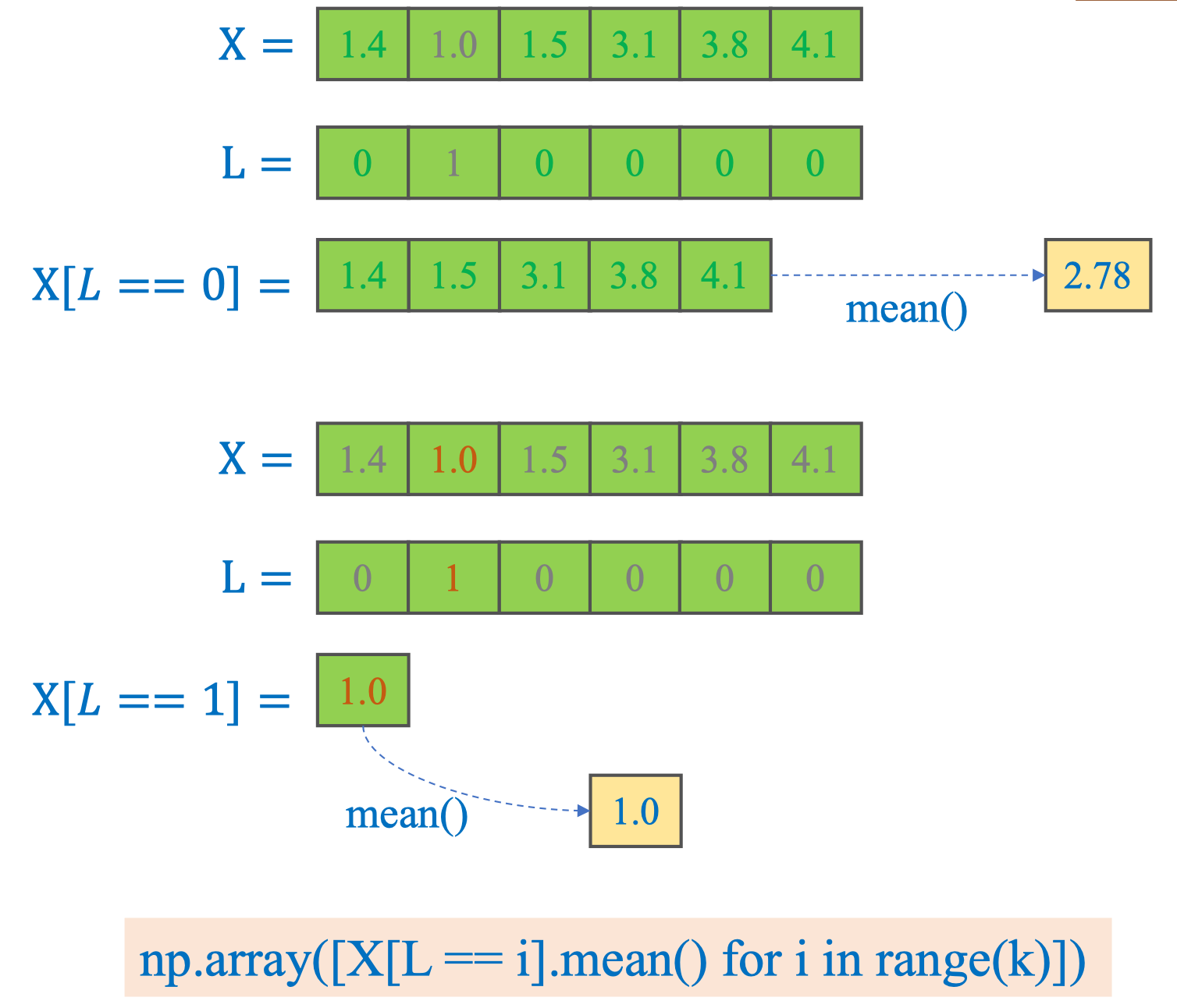

Cách 2 — Vector hóa nhanh bằng **np.bincount** (không vòng lặp Python):

sums = np.bincount(L, weights=X, minlength=k)   # tổng X theo từng nhãn
counts = np.bincount(L, minlength=k)            # số phần tử mỗi nhãn
C_new = sums / counts                           # trung bình
print(C_new)  # [2.78 1.  ]

💡 Tip: Khi một cụm rỗng (counts[i] = 0), cần xử lý đặc biệt: khởi tạo lại centroid (ví dụ lấy điểm xa nhất, điểm ngẫu nhiên, hoặc tâm của cụm lớn nhất) để tránh chia cho 0.

• Câu hỏi gợi mở
  1. Bạn sẽ xử lý trường hợp cụm rỗng theo chiến lược nào để ổn định hội tụ?
  2. So sánh hiệu năng bincount với list-comprehension khi n lớn (10⁶). Khi nào nên chọn cách nào?
  3. Làm sao mở rộng cập nhật centroid cho dữ liệu nhiều chiều (X có shape n×d) mà vẫn tránh vòng lặp Python?

Kiểm tra điều kiện dừng với np.all

Mục tiêu: dừng vòng lặp khi centroid không đổi giữa hai lần cập nhật.

import numpy as np
C     = np.array([1.4, 1.0])
C_new = np.array([2.78, 1.0])
print(C == C_new)          # [False  True]
print(np.all([True, True]))   # True
print(np.all([False, True]))  # False
# Điều kiện dừng
if np.all(C == C_new):
    break

Diễn giải:

• So sánh phần tử: C == C_new → [False, True].
• Gộp toàn cục: np.all(...) trả về False, nên chưa dừng (vì còn phần tử khác nhau).

Tip: Với số thực, nên dùng np.allclose(C, C_new, atol=1e-6) để tránh lỗi do sai số dấu phẩy động.

• Câu hỏi gợi mở
  1. Khi dùng np.allclose, bạn chọn atol/rtol thế nào để cân bằng giữa độ chính xác và tốc độ hội tụ?
  2. Nếu thứ tự centroids bị tráo đổi (permutation), điều kiện dừng cần điều chỉnh ra sao?
  3. Ngoài so sánh centroids, có thể dừng theo mức giảm hàm mục tiêu hoặc nhãn không đổi — trường hợp nào đáng tin cậy hơn?

Tính WCSS (Within-Cluster Sum of Squares) bằng NumPy

WCSS đo độ chặt của các cụm: tổng bình phương khoảng cách từ mỗi điểm tới centroid cụm của nó. Công thức (cho S = (S₀, S₁, …), centroids cᵢ): 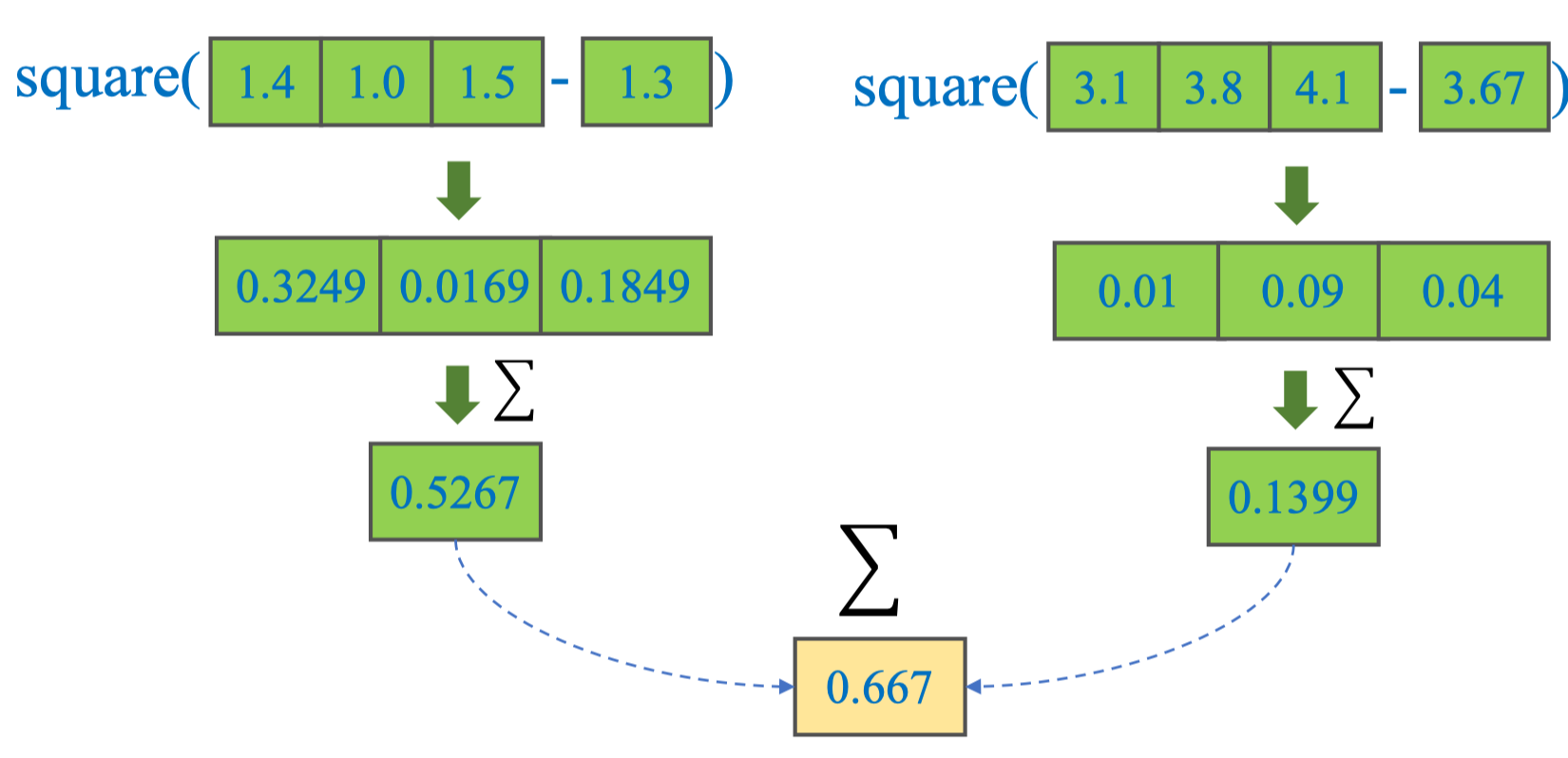$WCSS=\sum {i=0}^{k-1}\sum x\in S_i\Vert x-c_i{\Vert }^2$ Cách 1 — Theo cụm (boolean indexing)

import numpy as np
X = np.array([1.4, 1.0, 1.5, 3.1, 3.8, 4.1], dtype=float)
L = np.array([1, 1, 1, 0, 0, 0], dtype=int)
C = np.array([3.67, 1.30], dtype=float)  # C0, C1
wcss = sum(np.sum((X[L == i] - C[i])**2) for i in range(len(C)))
print(round(wcss, 4))  # ~0.6670

Cách 2 — Vector hóa hoàn toàn (không vòng lặp Python) Ý tưởng: ánh xạ mỗi điểm tới centroid tương ứng bằng lập index C[L], rồi tính một lần.

wcss_vec = np.sum((X - C[L])**2)
print(round(wcss_vec, 4))  # ~0.6670

💡 Tip: Công thức vector hóa np.sum((X - C[L])**2) mở rộng trực tiếp cho dữ liệu nhiều chiều nếu X là (n, d) và C là (k, d): chỉ cần dùng broadcasting X - C[L].

• Câu hỏi gợi mở
  1. Bạn sẽ theo dõi độ giảm WCSS để đặt điều kiện dừng như thế nào (ví dụ: WCSS giảm < ε)?
  2. Với dữ liệu nhiều chiều (n, d), làm sao tính WCSS theo từng cụm để debug (in ra bảng như slide)?
  3. Liệu có lợi ích khi dùng chuẩn L₁ thay vì L₂ cho WCSS trong các bài toán có nhiễu/outlier mạnh?

II. 3. Features = 2, Clusters = 3

Phần này minh họa K-Means khi số thuộc tính (features) = 2 và số cụm (K) = 3. Dữ liệu mô tả mối quan hệ giữa tuổi (Age) và tỷ lệ chi tiêu hằng tháng (Expenditure %).

Dataset

Bảng dữ liệu gốc:

Index	Age	Expenditure (%)
1	18	80
2	20	90
3	22	85
4	30	50
5	34	64
6	40	60
7	60	30
8	66	40
9	70	25
Mô tả: Tập dữ liệu gồm 9 điểm trong không gian 2 chiều, mỗi điểm là một khách hàng với hai thuộc tính Age và Expenditure.
![[image 19 8.png	image 19 8.png]]
💡 Tip: Vì Age và Expenditure có thang đo khác nhau, nên chuẩn hóa/điều chuẩn (ví dụ: StandardScaler hoặc MinMaxScaler) trước khi chạy K-Means để tránh thuộc tính có thang lớn chi phối khoảng cách.

• Câu hỏi gợi mở
  1. Nếu không chuẩn hóa dữ liệu, cụm kết quả sẽ bị lệch theo thuộc tính nào và vì sao?
  2. Với K = 3, bạn dự đoán ranh giới cụm sẽ chia các điểm theo khu vực nào trên đồ thị tán xạ?
  3. Chỉ với 2 thuộc tính, nên dùng Elbow hay Silhouette để chọn K? Tại sao?

Targets

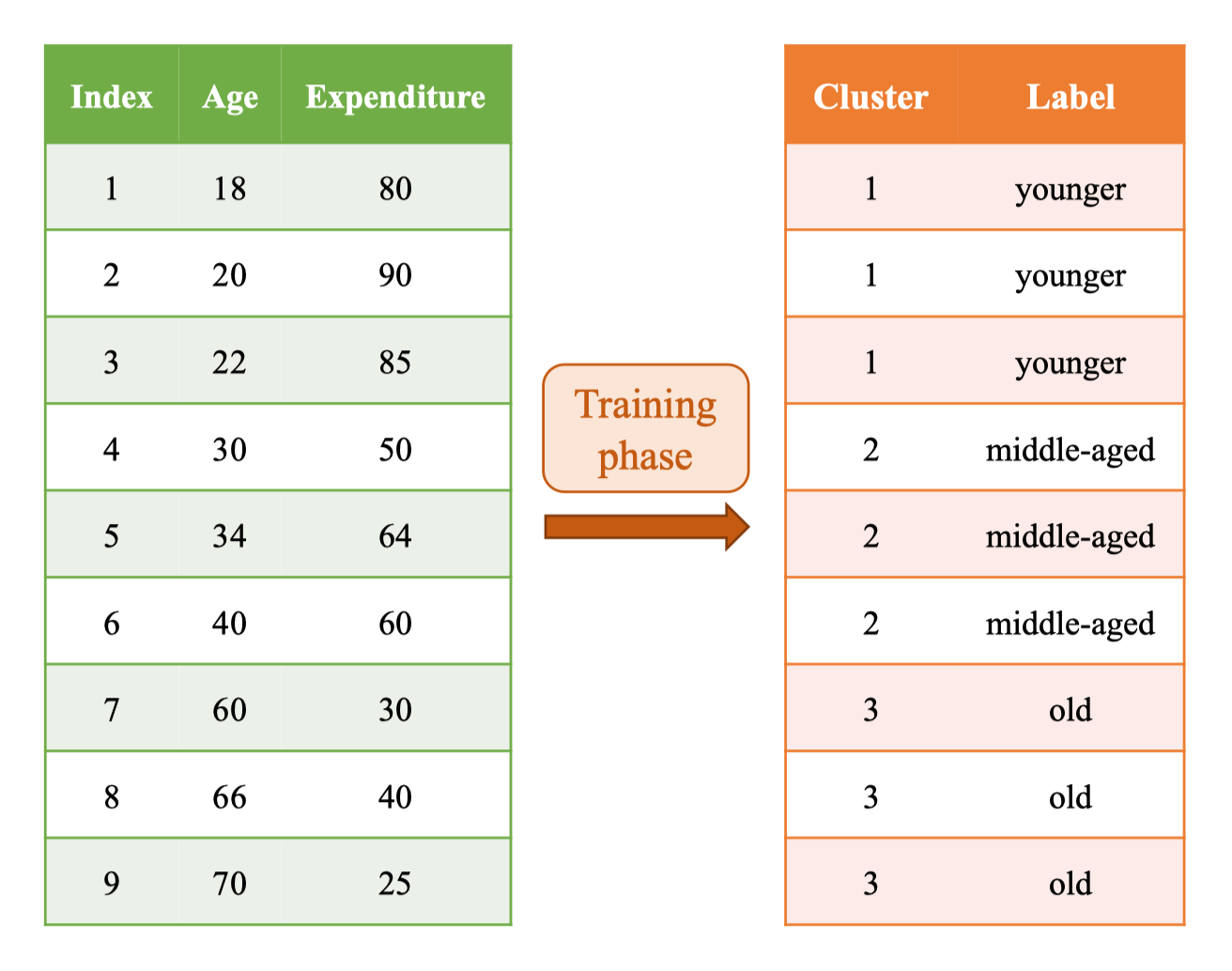
Trong training phase, sau khi chạy K-Means với K = 3, mỗi điểm dữ liệu được gán vào một cluster (1, 2, 3). Ta gắn ý nghĩa ngữ nghĩa cho từng cụm để phục vụ suy luận sau này. Bảng ánh xạ cluster → label:

Cluster	Label
1	younger
2	middle-aged
3	old

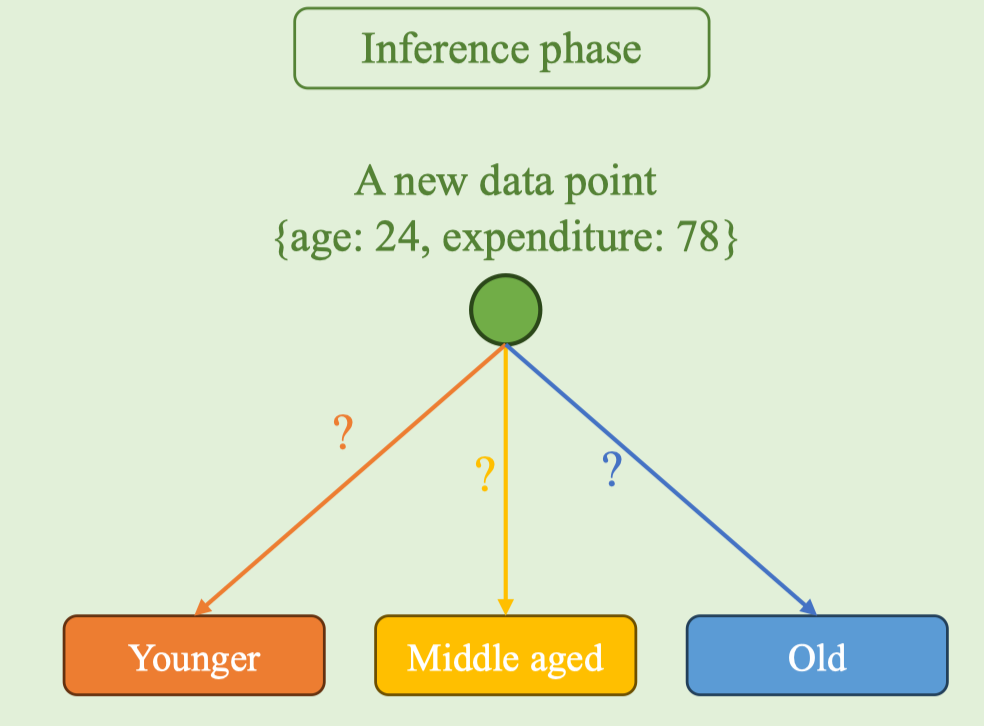
Trong inference phase, với điểm mới x = (age: 24, expenditure: 78), ta tính khoảng cách tới các centroids đã học và chọn cụm gần nhất: pred_cluster = argmin_j ‖x − c_j‖ pred_label = map[pred_cluster]

💡 Tip: Chỉ số cụm (1,2,3) có thể đổi thứ tự giữa các lần huấn luyện do khởi tạo khác nhau. Hãy lưu lại ánh xạ cluster→label sau khi train (hoặc sắp xếp centroid theo một tiêu chí ổn định, ví dụ theo Age tăng dần) để đảm bảo nhãn suy luận nhất quán.

• Câu hỏi gợi mở
  1. Nếu retrain khiến vị trí các centroid hoán đổi, bạn duy trì ánh xạ cluster→label thế nào cho ổn định?
  2. Ngoài gắn nhãn thủ công (younger/middle-aged/old), có tiêu chí tự động nào để đặt tên cụm từ thống kê của cụm (mean/median) không?
  3. Với dữ liệu thực tế có outlier, bạn sẽ gắn nhãn và kiểm định chất lượng cụm theo chỉ số nào (Silhouette, Davies–Bouldin, Calinski–Harabasz)?

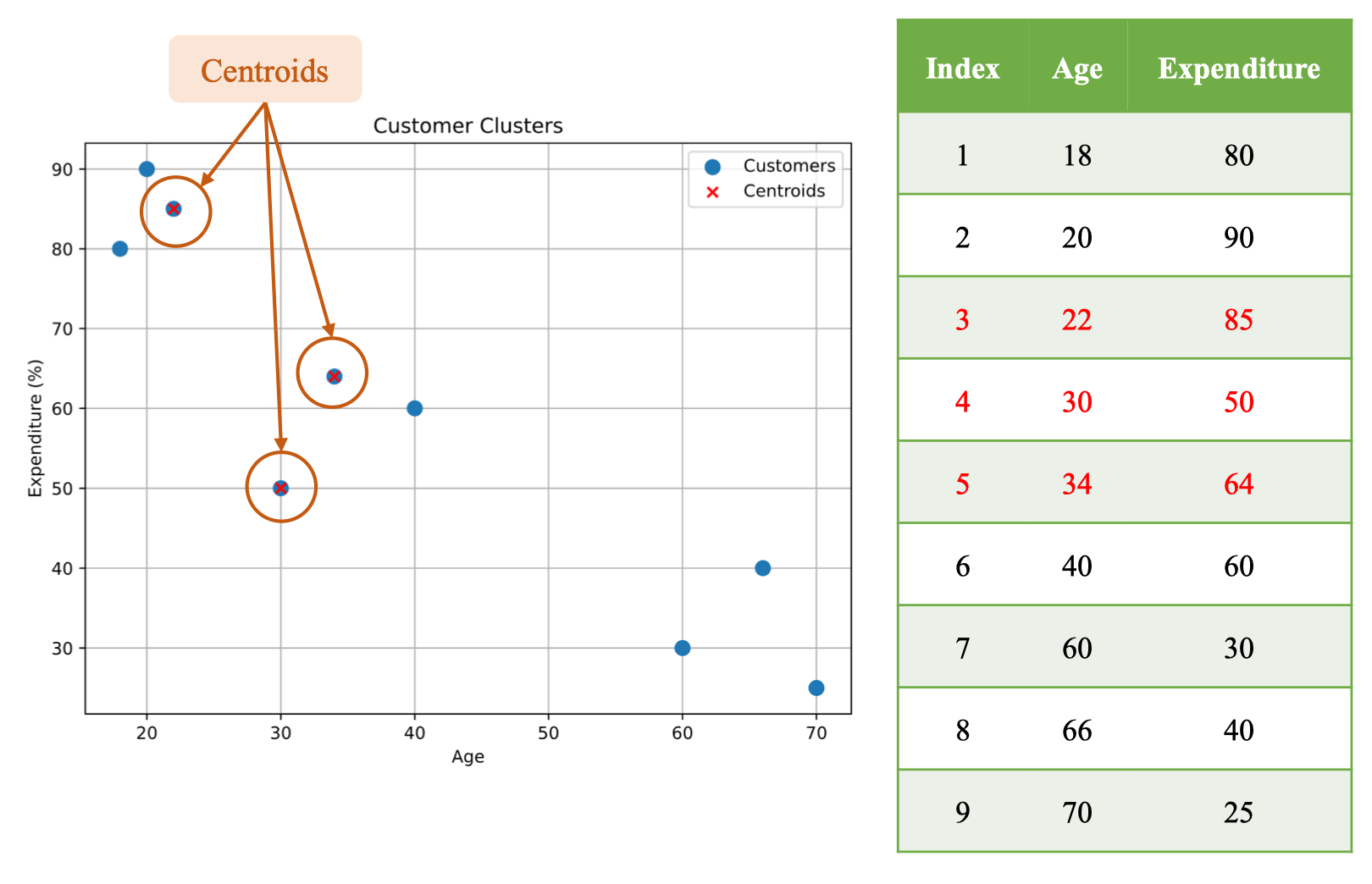
Step 1 — Init Centroids by random pickup

Khởi tạo K = 3 trọng tâm ban đầu bằng cách lấy ngẫu nhiên từ tập dữ liệu 2D (Age, Expenditure). Ba điểm được chọn làm centroids ban đầu là:

• C₀ = (22, 85)
• C₁ = (30, 50)
• C₂ = (34, 64)

Step 2 — Assign labels

Nhiệm vụ: với K = 3 và các centroids khởi tạo C₀ = (22, 85), C₁ = (30, 50), C₂ = (34, 64), hãy tính khoảng cách L2 từ từng điểm tới mỗi centroid và gán nhãn là chỉ số centroid gần nhất. Công thức (2D – L2): $\Vert x-c{\Vert }_2=\surd ((x_1-c_1{)}^2+(x_2-c_2{)}^2)$ Ví dụ minh họa (Data point 1: (18, 80))

• d((18,80), C₀) = √((18−22)² + (80−85)²) = √(16+25) ≈ 6.40

• d((18,80), C₁) = √((18−30)² + (80−50)²) = √(144+900) ≈ 32.31

• d((18,80), C₂) = √((18−34)² + (80−64)²) = √(256+256) ≈ 22.63

  → Điểm 1 thuộc cụm C₀ (label = 0).

Xét điểm dữ liệu #2: (Age = 20, Expenditure = 90) Khoảng cách: d((20, 90), C₀) = √((20 − 22)² + (90 − 85)²) = √(4 + 25) = √29 ≈ 5.39 d((20, 90), C₁) = √((20 − 30)² + (90 − 50)²) = √(100 + 1600) = √1700 ≈ 41.23 d((20, 90), C₂) = √((20 − 34)² + (90 − 64)²) = √(196 + 676) = √872 ≈ 29.53 Kết luận: Data point 2 gần C₀ nhất ⇒ Label = 0.

Centroid	Toạ độ	Khoảng cách
C₀	(22, 85)	5.39
C₁	(30, 50)	41.23
C₂	(34, 64)	29.53
Cập nhật hàng dữ liệu:
Index	Age	Expenditure
---	---	---
2	20	90
Bảng kết quả gán nhãn (vòng 1):
Index	Age	Expenditure
---	---	---
1	18	80
2	20	90
3	22	85
4	30	50
5	34	64
6	40	60
7	60	30
8	66	40
9	70	25
![[image 23 5.png	image 23 5.png]]

Code:

import numpy as np
X = np.array([[18,80],[20,90],[22,85],[30,50],[34,64],[40,60],[60,30],[66,40],[70,25]], float)  # (n,2)
C = np.array([[22,85],[30,50],[34,64]], float)                                                # (K,2)
D = np.linalg.norm(X[:, None, :] - C[None, :, :], axis=2)  # (n,K) khoảng cách L2
labels = D.argmin(axis=1)                                   # (n,) nhãn gần nhất

💡 Tip: Với dữ liệu 2D trở lên, nên chuẩn hóa từng feature trước khi tính khoảng cách; dùng X[:,None,:] - C[None,:,:] để broadcasting thành ma trận khoảng cách (n×K) và chọn nhãn bằng argmin(axis=1).

• Câu hỏi gợi mở
  1. Nếu hai centroids cách điểm như nhau (hòa), bạn sẽ “bẻ hòa” theo quy tắc nào để kết quả ổn định?
  2. Khi chuẩn hóa dữ liệu, bạn sẽ lưu centroids ở không gian chuẩn hóa hay gốc để dùng suy luận?
  3. So sánh tốc độ/nhớ giữa cách tính bằng np.linalg.norm và tự bình phương–cộng–căn thủ công với broadcasting.

Step 3 — Update Centroids (vòng 1)

Sau khi gán nhãn ở bước trước, ta cập nhật lại centroid của từng cụm bằng trung bình vector các điểm trong cụm. Công thức: $c_i^{(t+1)}=1/|S_i^{(t)}|{\sum }_{x\in S_i^{(t)}}x$ Các cụm ở vòng 1:

• Cụm 0 (label 0): (18,80), (20,90), (22,85)

  → $C_0^{new}=((18+20+22)/3,(80+90+85)/3)=(20,85)$

• Cụm 1 (label 1): (30,50), (60,30), (66,40), (70,25)

  → $C_1^{new}=((30+60+66+70)/4,(50+30+40+25)/4)=(56.5,36.25)$

• Cụm 2 (label 2): (34,64), (40,60)

  → $C_2^{new}=((34+40)/2,(64+60)/2)=(37,62)$

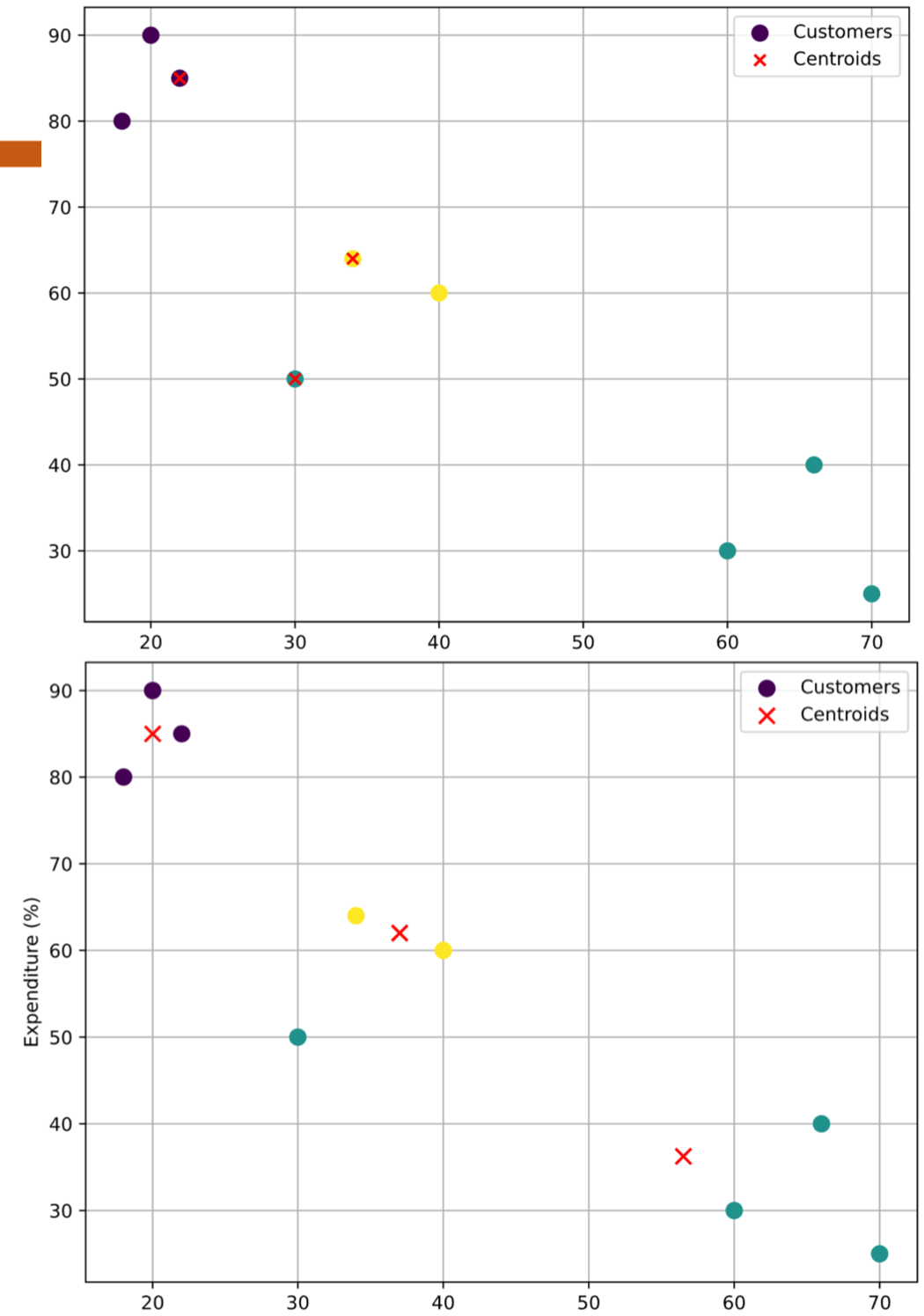
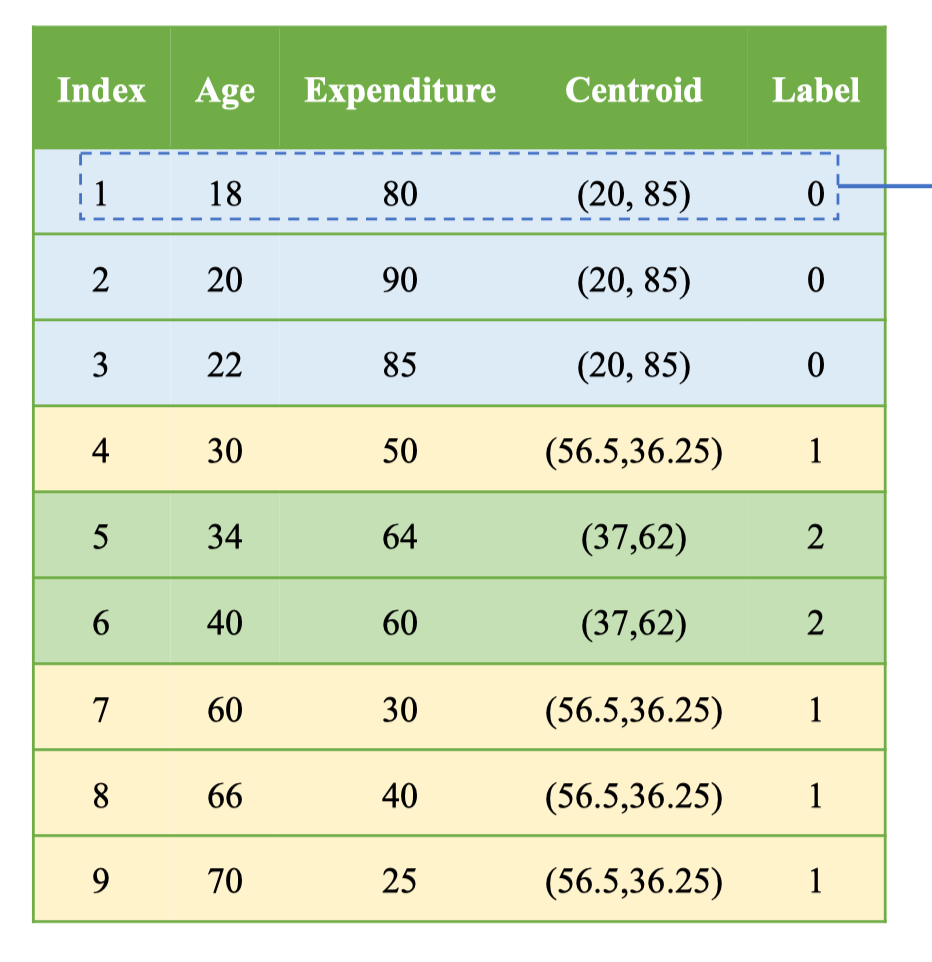
Bảng kết quả sau khi cập nhật centroid (giá trị “Centroid” là tọa độ mới ứng với nhãn của từng điểm):

Index	Age	Expenditure	Centroid	Label
1	18	80	(20, 85)	0
2	20	90	(20, 85)	0
3	22	85	(20, 85)	0
4	30	50	(56.5, 36.25)	1
5	34	64	(37, 62)	2
6	40	60	(37, 62)	2
7	60	30	(56.5, 36.25)	1
8	66	40	(56.5, 36.25)	1
9	70	25	(56.5, 36.25)	1
![[image 24 5.png	image 24 5.png]]

Repeat Step 2 — Calculate distance (vòng 2)

Centroids mới từ bước cập nhật: C₀ = (20, 85), C₁ = (56.5, 36.25), C₂ = (37, 62) Tính L2-distance cho điểm #1: x₁ = (18, 80). ‖x₁ − C₀‖₂ = √((18−20)² + (80−85)²) ≈ 5.38 ‖x₁ − C₁‖₂ = √((18−56.5)² + (80−36.25)²) ≈ 58.27 ‖x₁ − C₂‖₂ = √((18−37)² + (80−62)²) ≈ 26.17 Kết luận: Data point 1 gần Centroid 0 nhất ⇒ Label = 0 (không đổi so với vòng trước).

import numpy as np
x1 = np.array([18., 80.])
C  = np.array([[20., 85.], [56.5, 36.25], [37., 62.]])
d = np.linalg.norm(C - x1, axis=1)   # [5.38..., 58.27..., 26.17...]
label = d.argmin()                   # 0

💡 Tip: Sau khi cập nhật centroid, việc gán lại nhãn cho toàn bộ điểm là cần thiết để tiến đến hội tụ. Có thể vector hóa cho toàn bộ tập: labels = np.linalg.norm(X[:,None,:]-C[None,:,:], axis=2).argmin(1).

• Câu hỏi gợi mở
  1. Điểm nào có khả năng đổi cụm sau khi centroids mới được cập nhật (gần ranh giới giữa C₁ và C₂)?
  2. Nếu dùng chuẩn hoá Min-Max trước khi tính khoảng cách, các kết quả distance cho điểm #1 có thay đổi thứ tự không?
  3. Ta nên dừng khi nhãn toàn bộ điểm không đổi hay khi centroids không đổi (np.allclose) — tiêu chí nào phù hợp hơn cho bộ dữ liệu này?