Table
Important
Tham khảo
1. General Information
1.x. Time series Types
Time series Tasks
2. Data Generation
Trong xử lý chuỗi thời gian, Data Augmentation là quá trình áp dụng các phép biến đổi để tạo ra các mẫu mới. Điều này giúp tăng kích thước và đa dạng dữ liệu, từ đó làm cho mô hình trở nên mạnh mẽ hơn và giảm nguy cơ overfitting.
2.1. Data Augmentation – Basic Approaches
Ground truth
Chuỗi dữ liệu gốc (không biến đổi) được coi là baseline để so sánh hiệu quả của các phương pháp tăng cường dữ liệu.
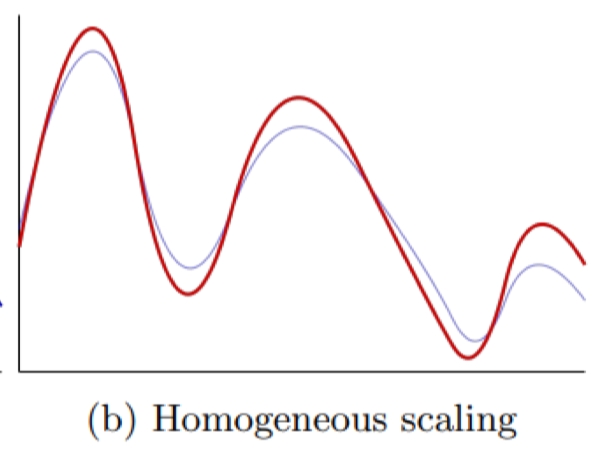
 Homogeneous scaling
Phương pháp này thực hiện việc co giãn đồng đều biên độ của toàn bộ chuỗi, giúp mô hình học được tính linh hoạt về cường độ.
Homogeneous scaling
Phương pháp này thực hiện việc co giãn đồng đều biên độ của toàn bộ chuỗi, giúp mô hình học được tính linh hoạt về cường độ.
 Rotation
Biến đổi bằng cách đảo ngược hoặc xoay tín hiệu theo trục, giúp mô hình tránh phụ thuộc quá mức vào hướng của chuỗi.
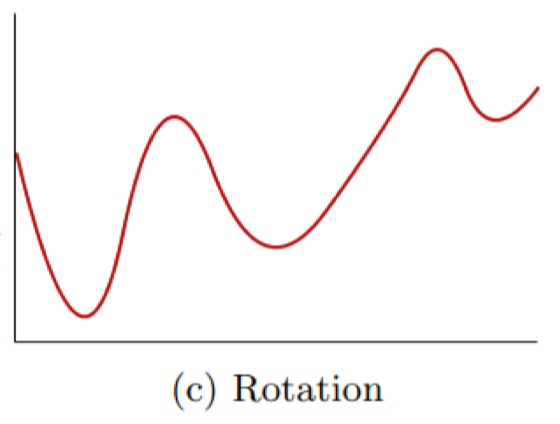
Rotation
Biến đổi bằng cách đảo ngược hoặc xoay tín hiệu theo trục, giúp mô hình tránh phụ thuộc quá mức vào hướng của chuỗi.
 Jittering
Thêm nhiễu ngẫu nhiên vào tín hiệu gốc để tạo sự đa dạng, tương tự như dữ liệu thực tế vốn chứa nhiễu đo lường.
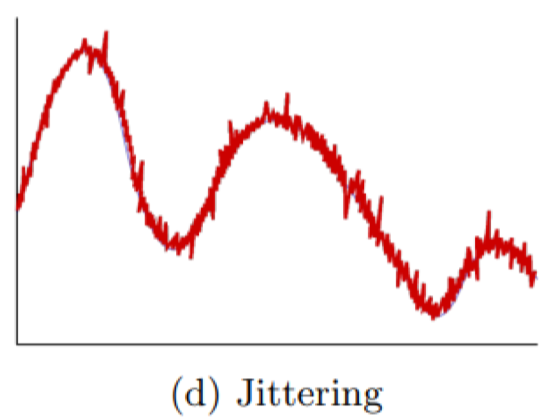
Jittering
Thêm nhiễu ngẫu nhiên vào tín hiệu gốc để tạo sự đa dạng, tương tự như dữ liệu thực tế vốn chứa nhiễu đo lường.
 Magnitude warping
Áp dụng hàm phi tuyến lên biên độ, tạo ra sự thay đổi cục bộ trong độ lớn của chuỗi.
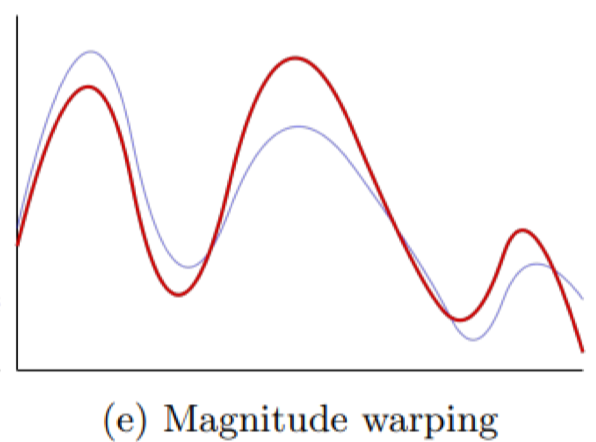
Magnitude warping
Áp dụng hàm phi tuyến lên biên độ, tạo ra sự thay đổi cục bộ trong độ lớn của chuỗi.
 Time warping
Kéo giãn hoặc nén trục thời gian, làm thay đổi tốc độ dao động nhưng vẫn giữ nguyên hình dạng tổng thể.
Time warping
Kéo giãn hoặc nén trục thời gian, làm thay đổi tốc độ dao động nhưng vẫn giữ nguyên hình dạng tổng thể.
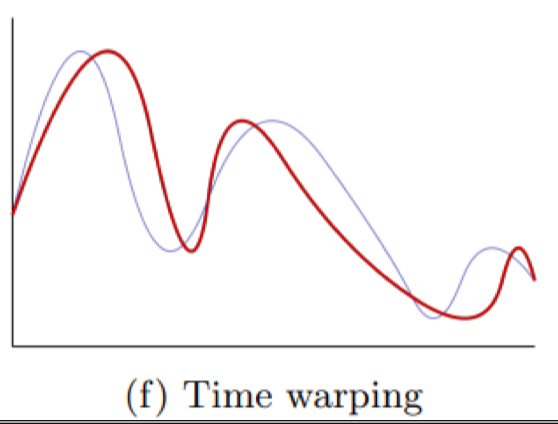 Permutation
Chia tín hiệu thành nhiều đoạn nhỏ và xáo trộn thứ tự, từ đó làm tăng khả năng mô hình học được tính không tuần tự.
Permutation
Chia tín hiệu thành nhiều đoạn nhỏ và xáo trộn thứ tự, từ đó làm tăng khả năng mô hình học được tính không tuần tự.
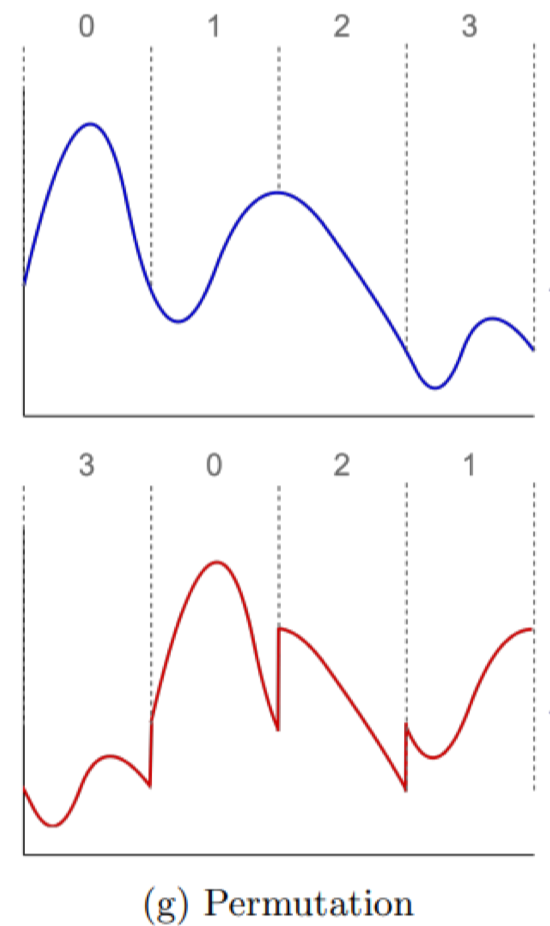 Window warping
Chọn một cửa sổ con trong chuỗi và co giãn riêng phần đó, giúp mô hình nhận diện sự biến đổi cục bộ.
Window warping
Chọn một cửa sổ con trong chuỗi và co giãn riêng phần đó, giúp mô hình nhận diện sự biến đổi cục bộ.
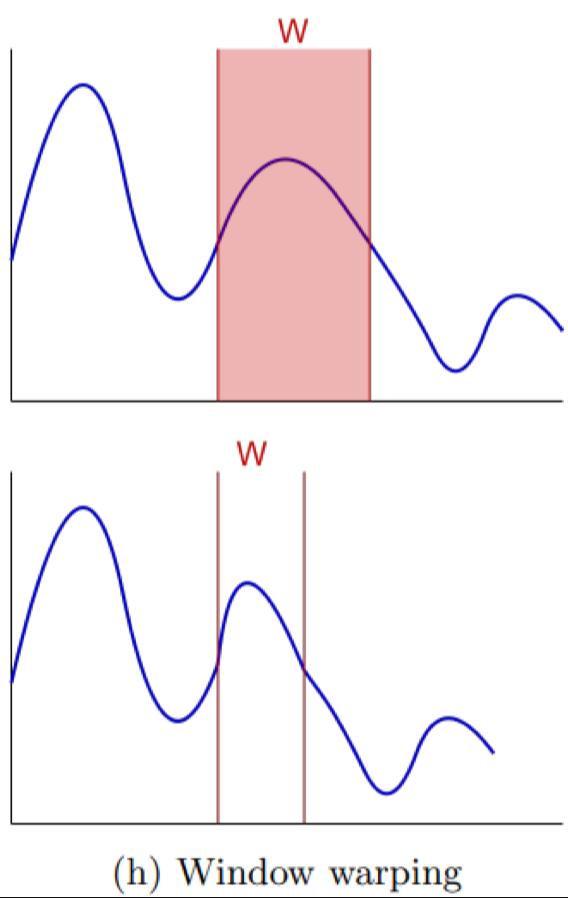 Time slicing window
Cắt tín hiệu thành nhiều cửa sổ con để tăng số lượng mẫu huấn luyện, đặc biệt hữu ích khi dữ liệu ban đầu nhỏ.
Time slicing window
Cắt tín hiệu thành nhiều cửa sổ con để tăng số lượng mẫu huấn luyện, đặc biệt hữu ích khi dữ liệu ban đầu nhỏ.
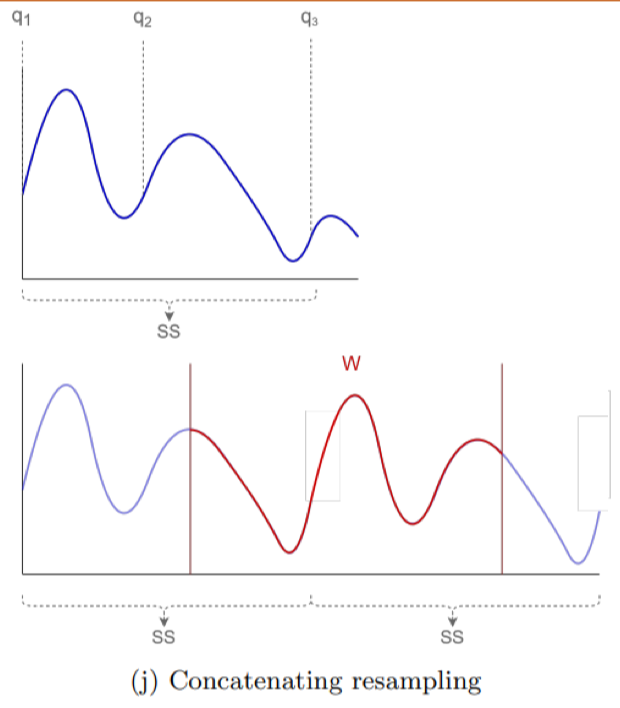
 Concatenating resampling
Kết hợp các đoạn con bằng cách resampling và nối chuỗi, giúp mô hình học được tính đa dạng theo chiều dài.
Concatenating resampling
Kết hợp các đoạn con bằng cách resampling và nối chuỗi, giúp mô hình học được tính đa dạng theo chiều dài.
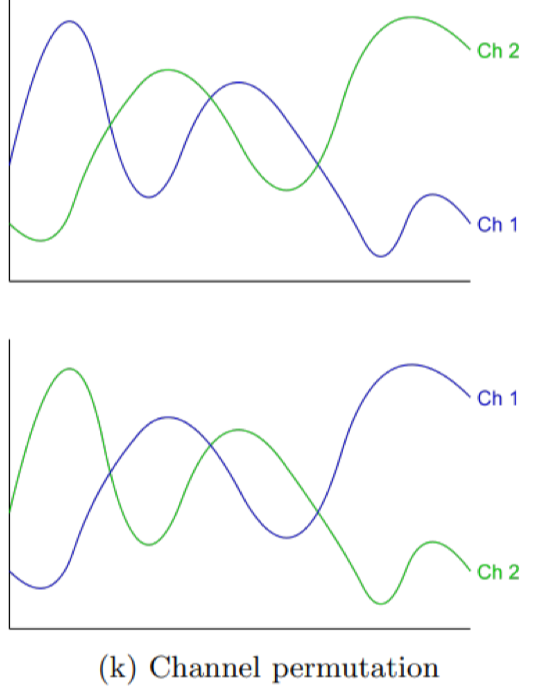
 Channel permutation
Trong dữ liệu đa kênh, thay đổi thứ tự các kênh để tạo mẫu mới, giúp mô hình không bị phụ thuộc vào thứ tự kênh.
Channel permutation
Trong dữ liệu đa kênh, thay đổi thứ tự các kênh để tạo mẫu mới, giúp mô hình không bị phụ thuộc vào thứ tự kênh.
2.2. Data Augmentation – Decomposition
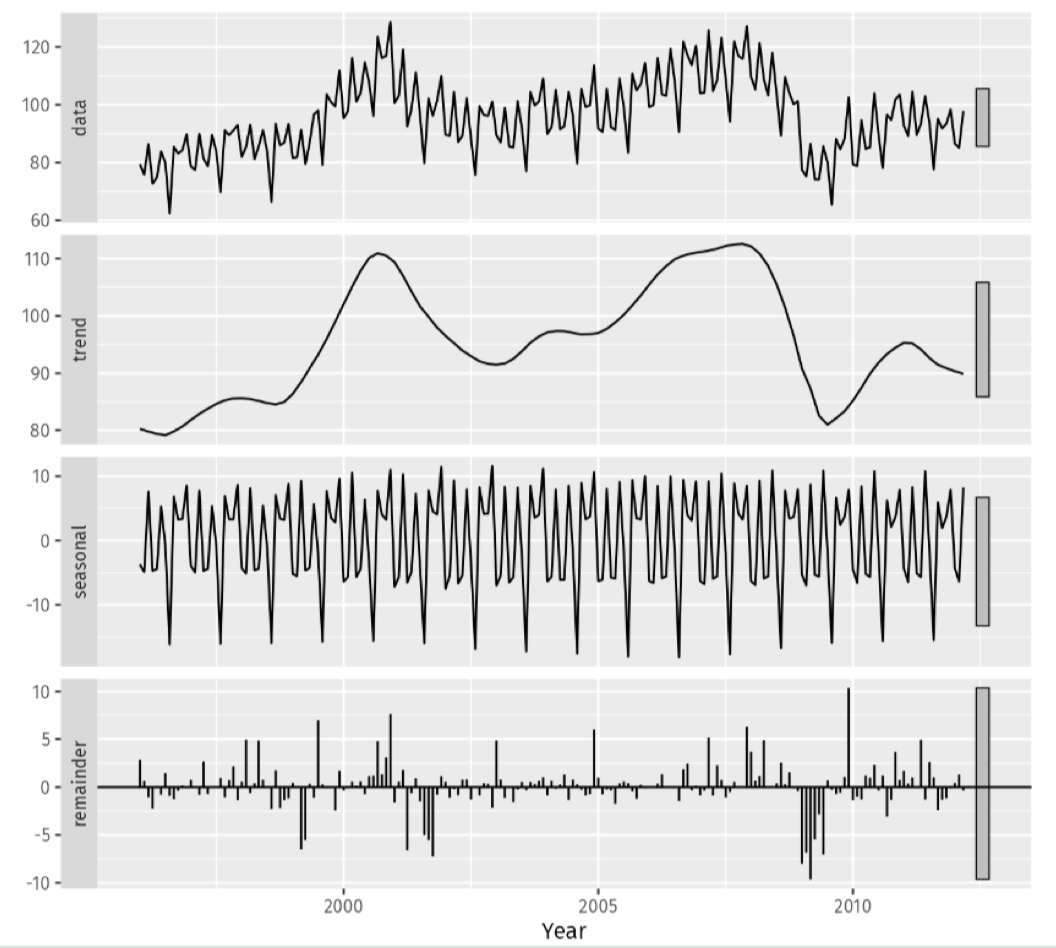
Một hướng tiếp cận khác để tăng cường dữ liệu chuỗi thời gian là phân rã (decomposition). Ý tưởng là tách chuỗi gốc thành các thành phần cơ bản như xu hướng (trend), mùa vụ (seasonal) và nhiễu (residual), sau đó biến đổi hoặc kết hợp lại để tạo mẫu mới. STL – Seasonal and Trend decomposition using Loess
- STL tách chuỗi thời gian thành 4 thành phần: Data, Trend, Seasonal, Remainder.
- Thích hợp khi độ biến thiên mùa vụ và phần dư (residuals) tương đối ổn định theo thời gian. Công thức: Trong đó:
- S: thành phần mùa vụ
- T: thành phần xu hướng
- R: phần dư (nhiễu)
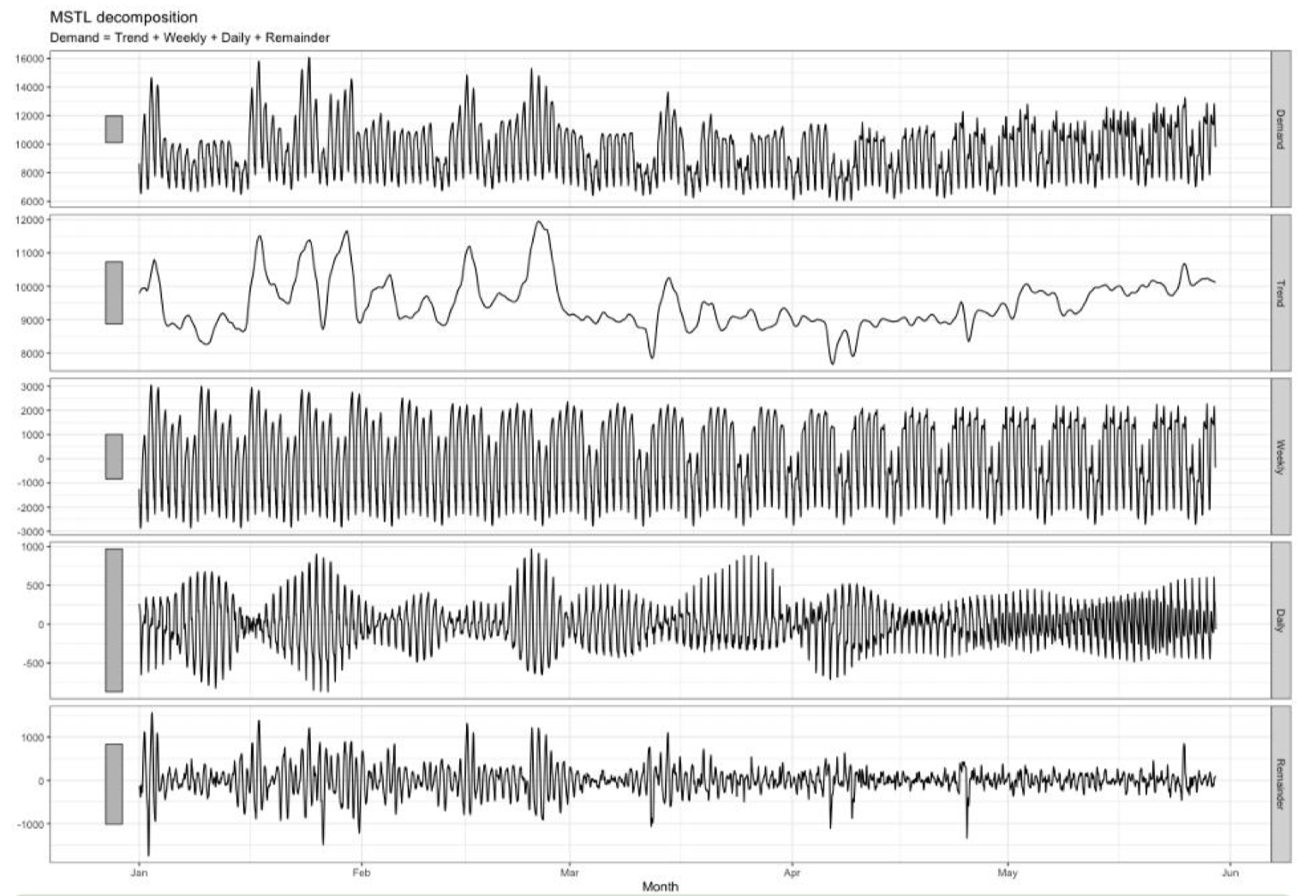
 MSTL – Trend and Multiple Seasonal decomposition using Loess
MSTL – Trend and Multiple Seasonal decomposition using Loess
- MSTL mở rộng STL, cho phép tách nhiều thành phần mùa vụ (daily, weekly, yearly, v.v.) cùng lúc.
- Hữu ích khi dữ liệu có chu kỳ lặp lại phức tạp (ví dụ: nhu cầu điện có biến động theo ngày và theo tuần).
- Phù hợp khi biến thiên mùa vụ và phần dư thay đổi theo tỷ lệ của xu hướng (trend level). Công thức: Trong đó:
- S: nhiều thành phần mùa vụ (weekly, daily, yearly, …)
- T: thành phần xu hướng
- R: phần dư (nhiễu)
2.3. Data Condensation
Data Condensation là kỹ thuật nén tập dữ liệu huấn luyện quy mô lớn thành một tập nhỏ tổng hợp (synthetic set). Mục tiêu là vẫn giữ được khả năng biểu diễn của dữ liệu gốc để mô hình có thể đạt hiệu năng tương đương khi huấn luyện.
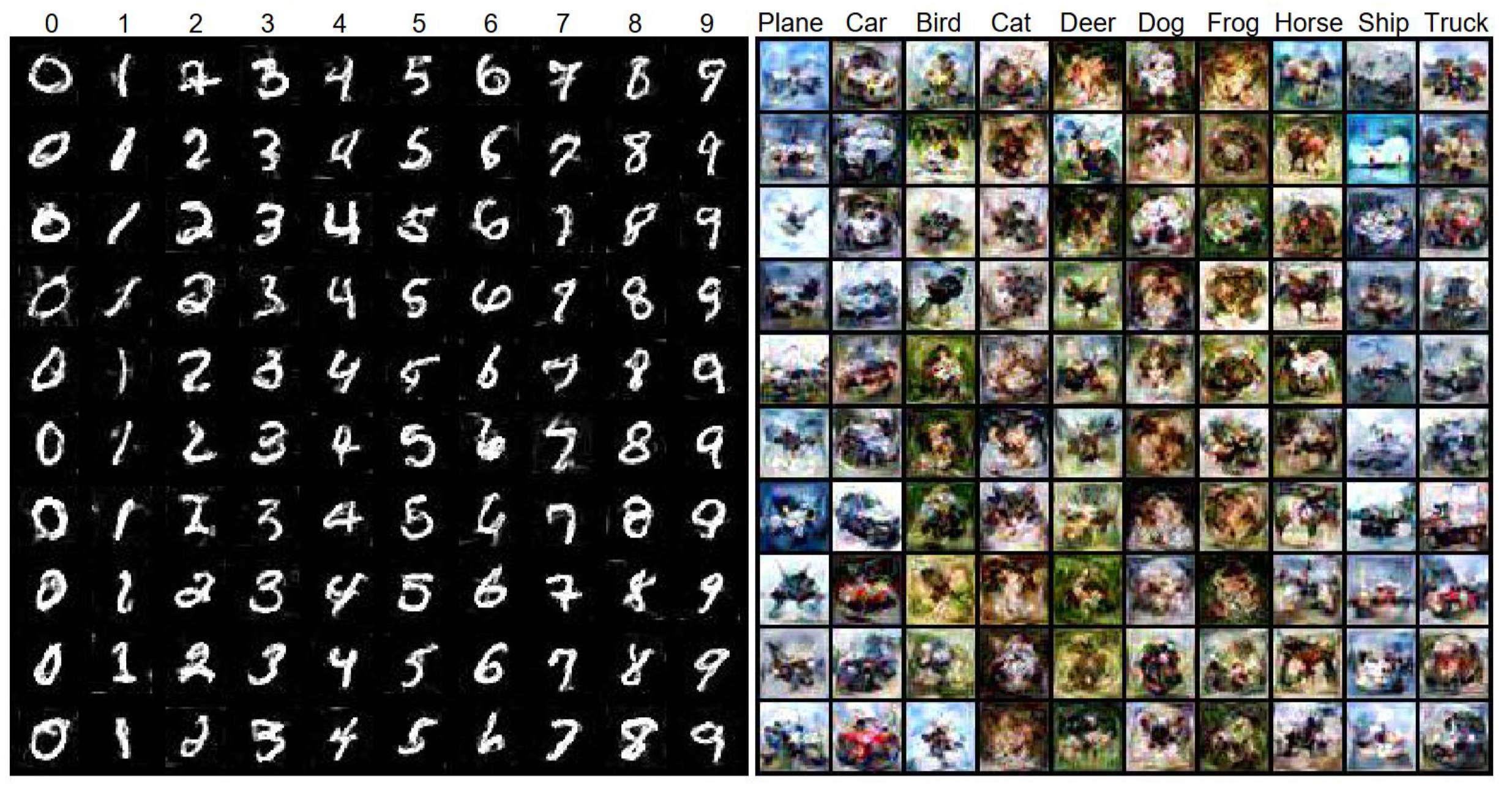
- Thay vì dùng hàng chục ngàn hoặc hàng triệu mẫu, ta tạo ra một số lượng nhỏ dữ liệu tổng hợp nhưng vẫn đủ giàu thông tin.
- Các mẫu tổng hợp này được sinh ra bằng các kỹ thuật tối ưu (ML,DL,…) , đảm bảo chúng đại diện tốt cho phân phối gốc. Ưu điểm:
- Giảm chi phí huấn luyện: tiết kiệm thời gian và tài nguyên tính toán.
- Chia sẻ dữ liệu tổng hợp: dễ dàng phân phối dữ liệu mà không cần toàn bộ tập gốc.
- Bảo vệ quyền riêng tư: dữ liệu gốc (có thông tin nhạy cảm) không cần phải chia sẻ, thay vào đó dùng dữ liệu tổng hợp. Nhược điểm:
- Distribution shift: dữ liệu tổng hợp có thể bị lệch phân phối so với dữ liệu thật, làm giảm độ chính xác.
- Cần kỹ thuật tối ưu để cân bằng giữa tính nhỏ gọn và độ đại diện của dữ liệu.
Lưu ý: Kĩ thuật này không thật sự tạo ra data mà nó là nén data lại.
3. Data Valuation
Data Valuation là quá trình định lượng và đánh giá giá trị của dữ liệu trong quá trình phân tích. Mục tiêu là xác định những đặc trưng quan trọng giúp mô hình học máy hoặc phân tích thống kê trở nên hiệu quả hơn. Khái niệm này bao gồm nhiều hướng tiếp cận khác nhau, trong đó phổ biến nhất là dựa trên đặc trưng thống kê, đặc trưng thời gian, hoặc các phương pháp tiên tiến như influence functions và Shapley value.
3.1. Data Valuation – Statistical Properties
Statistical Properties mô tả sự phân bố của các giá trị trong chuỗi dữ liệu, nhưng không phản ánh trực tiếp hành vi theo thời gian. Các đặc trưng này thường được dùng để tóm tắt, so sánh nhóm dữ liệu, phát hiện bất thường hoặc chuẩn hóa.
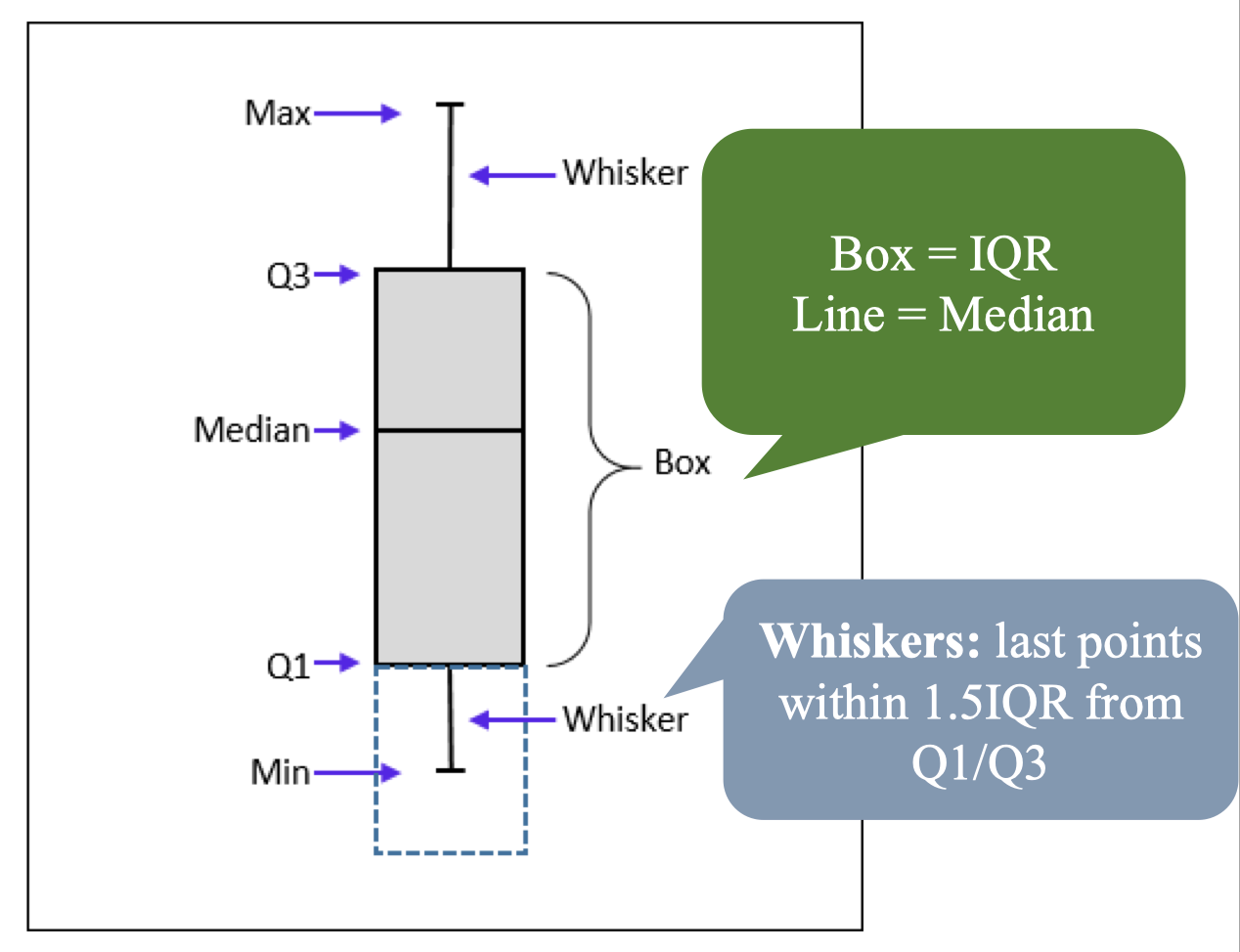
Các đặc trưng thống kê cơ bản
- Min: giá trị nhỏ nhất trong tập dữ liệu.
- Max: giá trị lớn nhất trong tập dữ liệu.
- Mean: trung bình cộng (tổng các giá trị chia cho số lượng).
- Median (Q2): trung vị, biểu diễn vị trí trung tâm, ít nhạy cảm với outlier.
- Range: khoảng giá trị, được tính bằng Max – Min.
- IQR (Interquartile Range): Q3 – Q1, thể hiện mức độ phân tán dữ liệu giữa tứ phân vị.
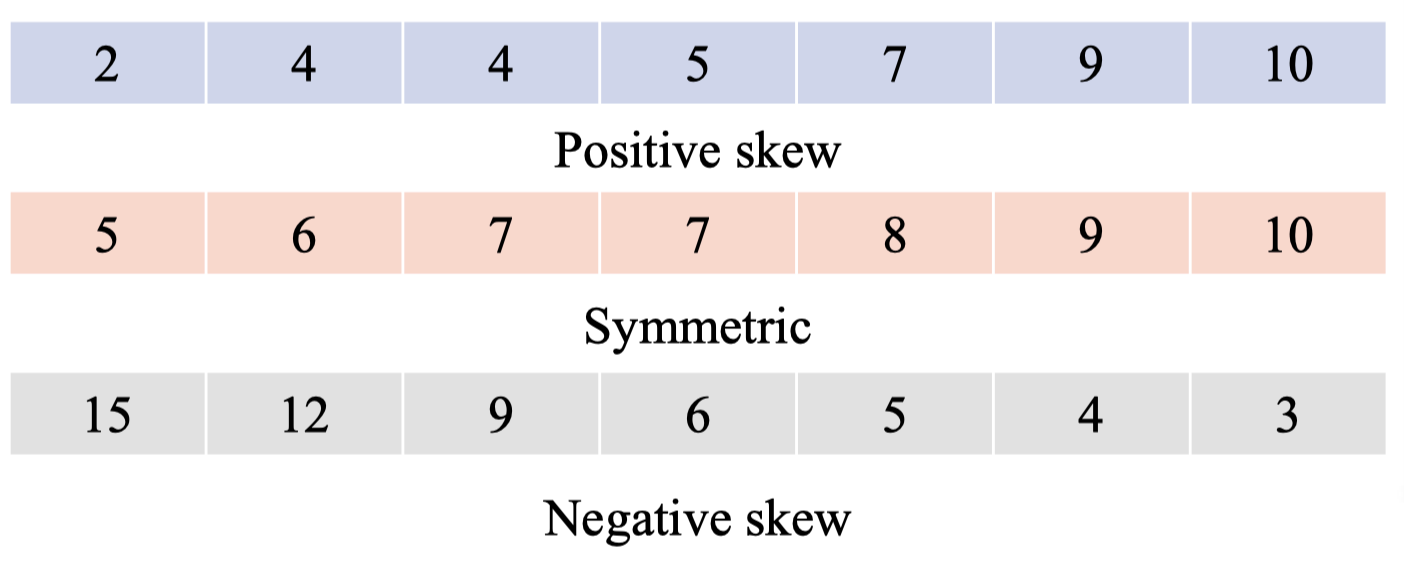
- Outlier: phần tử bất thường: Ví dụ: Với tập dữ liệu: 2, 4, 4, 5, 7, 9, 10
- Min = 2
- Max = 10
- Mean ≈ 5.86
- Median (Q2) = 5
- Range = 8
- Q1 = 4, Q3 = 9 → IQR = 5
 Ý nghĩa và ứng dụng:
Ý nghĩa và ứng dụng: - Dùng summary statistics để so sánh nhóm dữ liệu, phát hiện outlier, lựa chọn phương pháp chuẩn hóa.
- Các thống kê này không xét đến thứ tự thời gian, do đó sẽ được bổ sung bằng các phương pháp khai thác mẫu (temporal patterns) trong các bước sau.
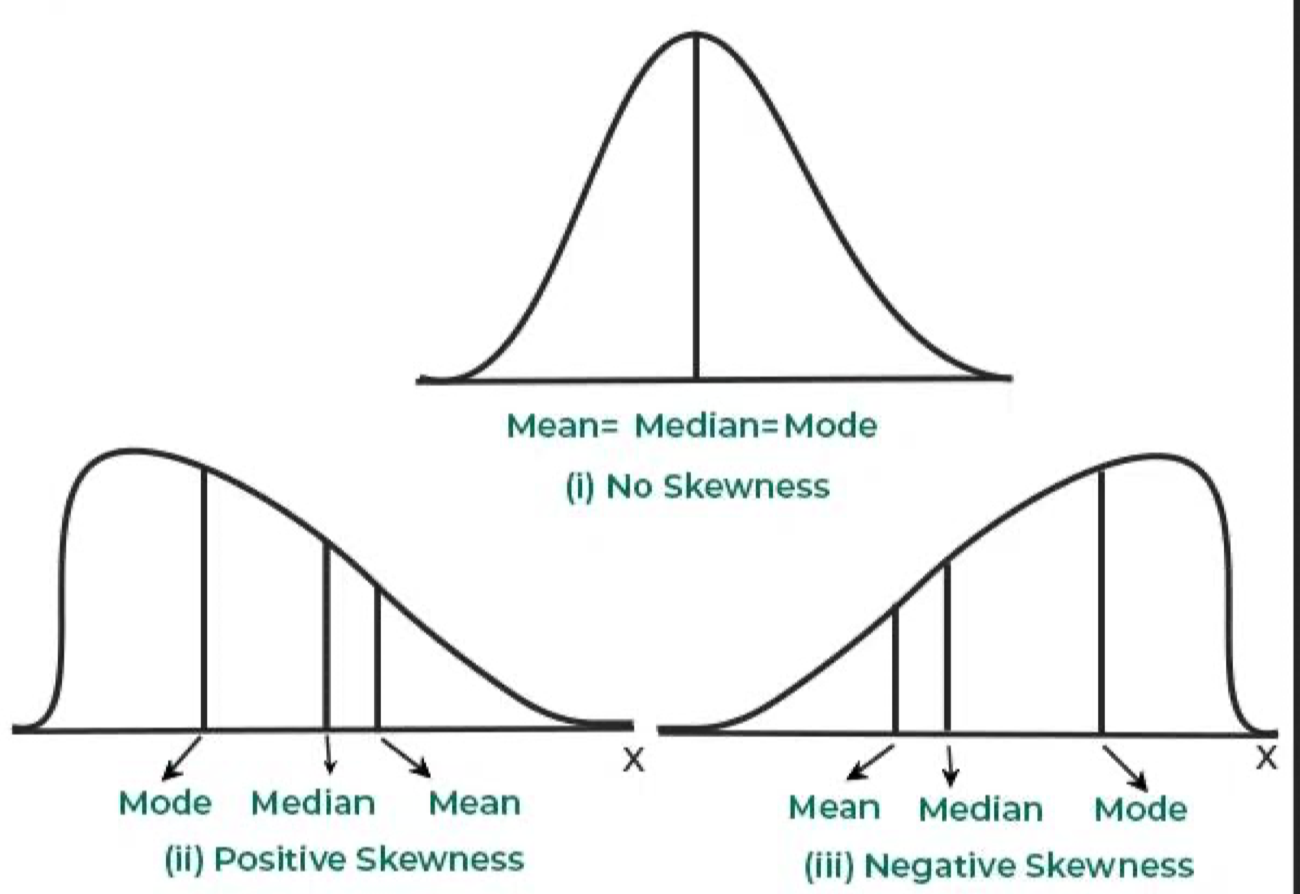
Skewness
Skewness đo lường mức độ bất đối xứng của phân phối dữ liệu. Đây là một đặc trưng quan trọng để nhận diện thiên lệch trong dữ liệu, đặc biệt trước khi áp dụng các kiểm định thống kê giả định dữ liệu tuân theo phân phối chuẩn.
- Positive skew (lệch phải): dữ liệu có đuôi dài về phía phải; Mean > Median > Mode.
- Negative skew (lệch trái): dữ liệu có đuôi dài về phía trái; Mean < Median < Mode.
- Zero skew (đối xứng): phân phối chuẩn, Mean = Median = Mode.
 Ví dụ:
Ví dụ:
 Ứng dụng
Ứng dụng
- Giúp nhận diện bias trong dữ liệu trước khi áp dụng các thuật toán hoặc kiểm định giả định tính chuẩn.
- Hỗ trợ lựa chọn phép biến đổi dữ liệu (ví dụ: log transform, Box-Cox transform) để đưa dữ liệu về gần phân phối chuẩn.
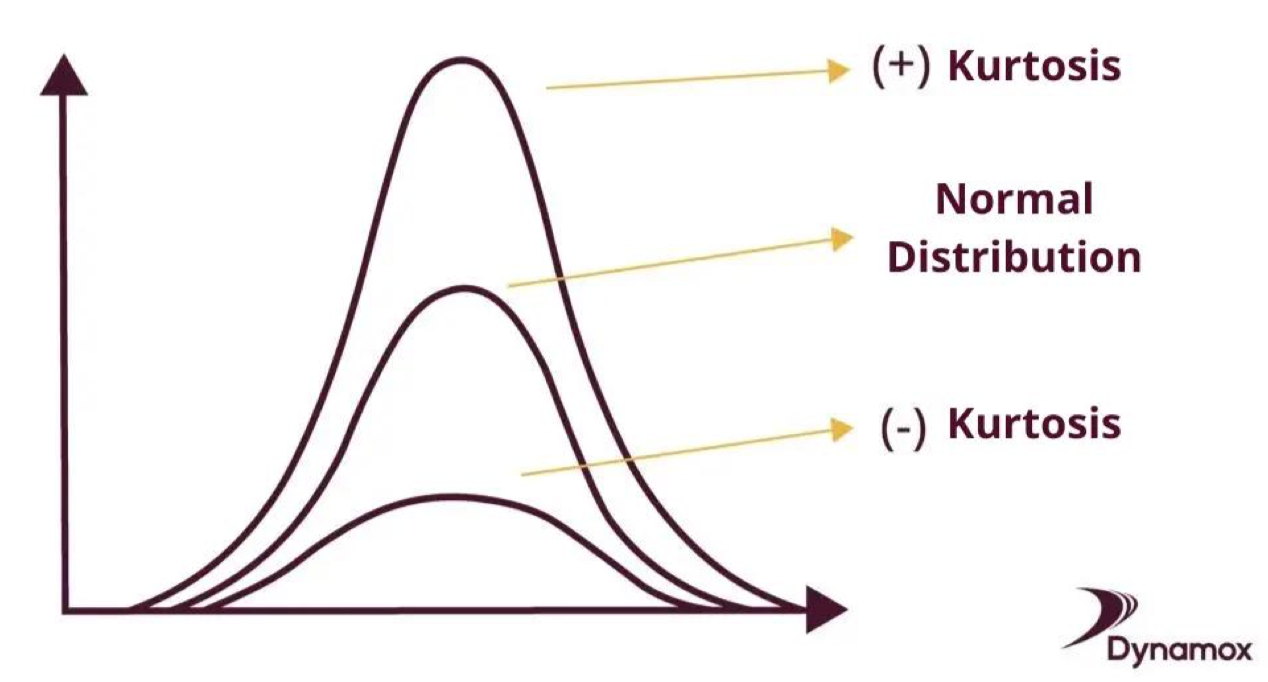
Kurtos
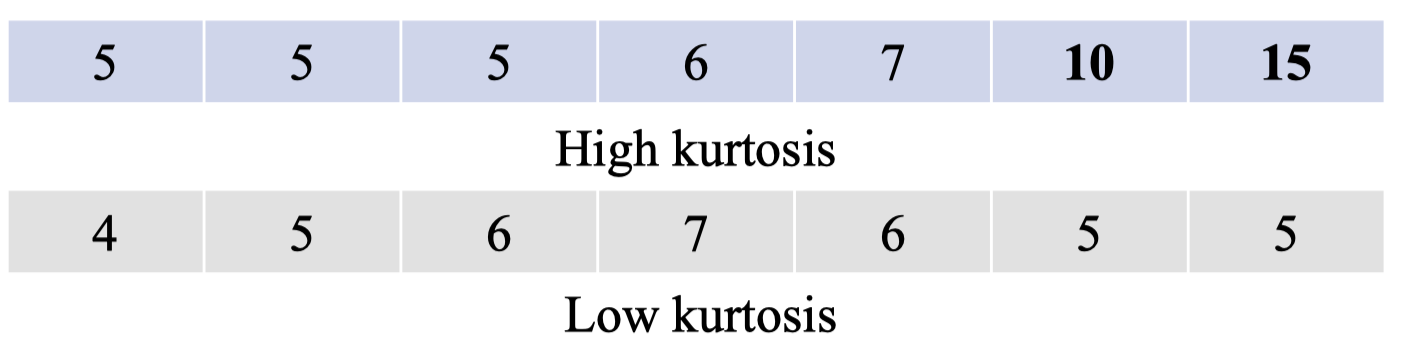
Kurtosis đo lường mức độ “nặng đuôi” (tailedness) hay “độ nhọn” (peakedness) của phân phối dữ liệu. Nó cho biết dữ liệu có xu hướng chứa nhiều giá trị cực đoan (outlier) hay không.
- High kurtosis (kurtosis lớn): phân phối có đỉnh nhọn, đuôi dày → nhiều outlier, rủi ro cao.
- Low kurtosis (kurtosis nhỏ): phân phối có đỉnh phẳng, đuôi nhẹ → ít outlier.
- Normal distribution: kurtosis ≈ 3 (nếu báo cáo excess kurtosis thì giá trị này ≈ 0).
 Ví dụ:
Ví dụ:
 Ứng dụng:
Ứng dụng: - Phát hiện outliers hoặc dữ liệu có đuôi nặng.
- Giúp đánh giá rủi ro trong các lĩnh vực như tài chính (đặc biệt với các biến động lớn).
- Kết hợp với skewness để xác định dữ liệu có tuân theo phân phối chuẩn hay không, từ đó lựa chọn phép kiểm định thống kê phù hợp.
3.2. Time Series Characteristics
Đặc trưng của chuỗi thời gian mô tả hành vi của dữ liệu theo thời gian hoặc cấu trúc tuần tự. Hai yếu tố quan trọng nhất là Seasonality (tính mùa vụ) và Trend (xu hướng).
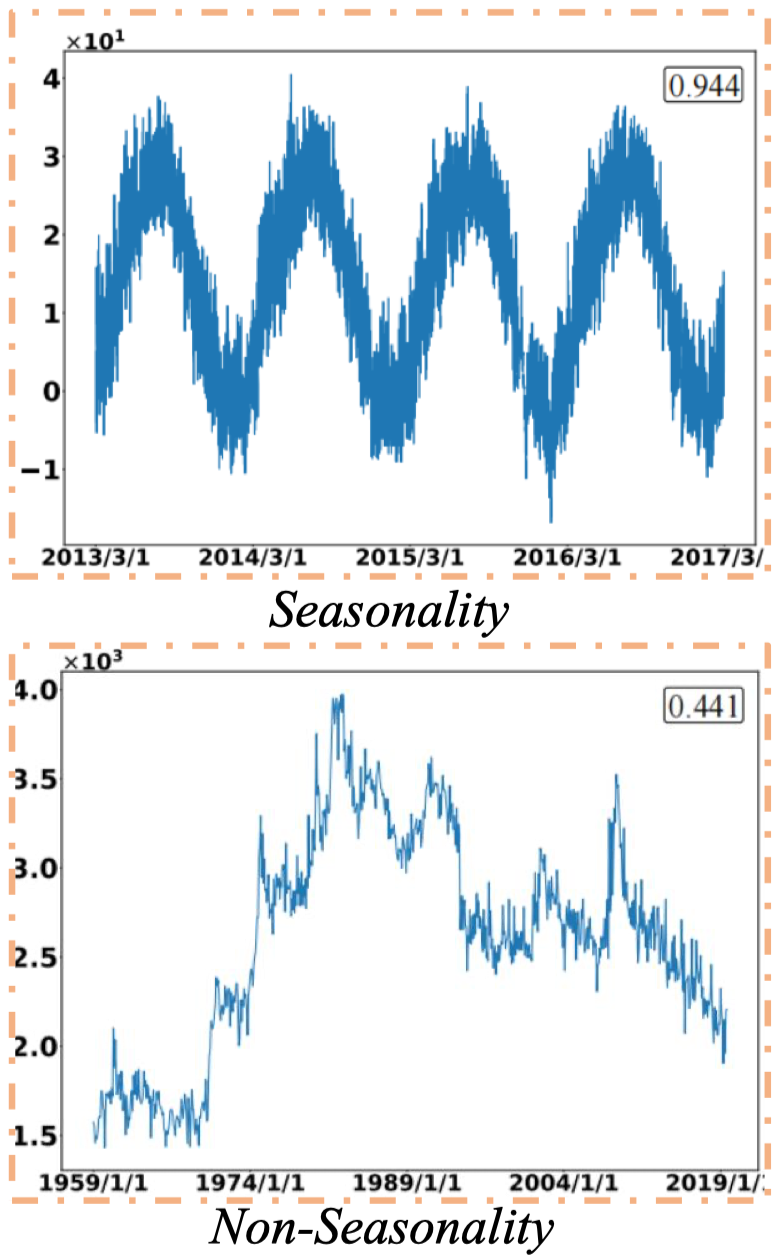
Seasonality và Non-Seasonality
- Seasonality: các mẫu lặp lại tại khoảng thời gian cố định.
- Ví dụ: “Doanh số kem đạt đỉnh vào mùa hè.”
- Non-Seasonality: biến động không có quy luật rõ ràng, khó dự đoán.
- Ví dụ: “Giá cổ phiếu dao động thất thường.”
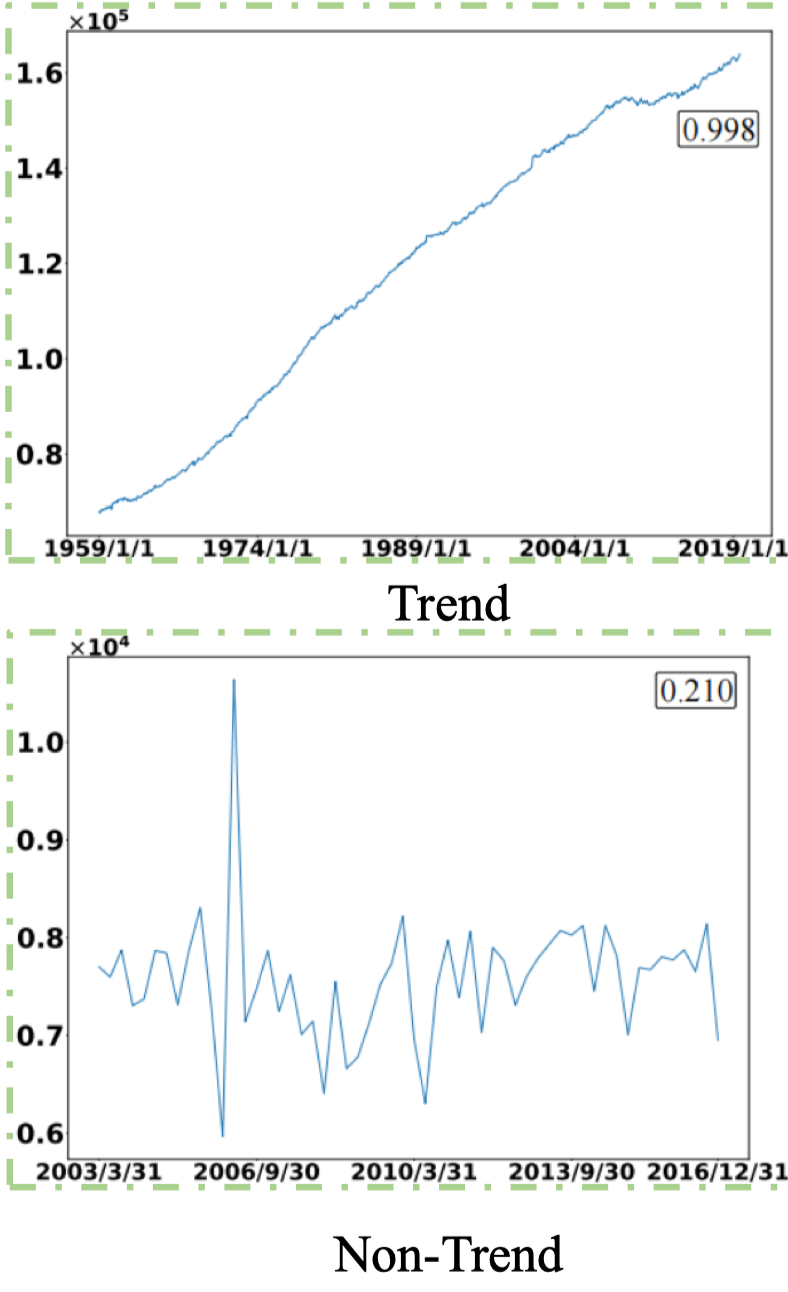
Trend và Non-Trend
- Trend: xu hướng tăng hoặc giảm dài hạn.
- Ví dụ: “Nhiệt độ trung bình toàn cầu tăng dần.”
- Non-Trend: dữ liệu chỉ chứa nhiễu ngẫu nhiên, không thể hiện hướng rõ ràng.
- Ví dụ: “Nhiễu hàng ngày trong dữ liệu cảm biến.”
 Việc xác định tính mùa vụ và xu hướng là bước quan trọng để:
Việc xác định tính mùa vụ và xu hướng là bước quan trọng để:
- Chọn mô hình dự báo phù hợp.
- Giúp phân rã dữ liệu (decomposition) để phân tích chi tiết.
- Tránh nhầm lẫn giữa nhiễu ngẫu nhiên và tín hiệu thực sự.
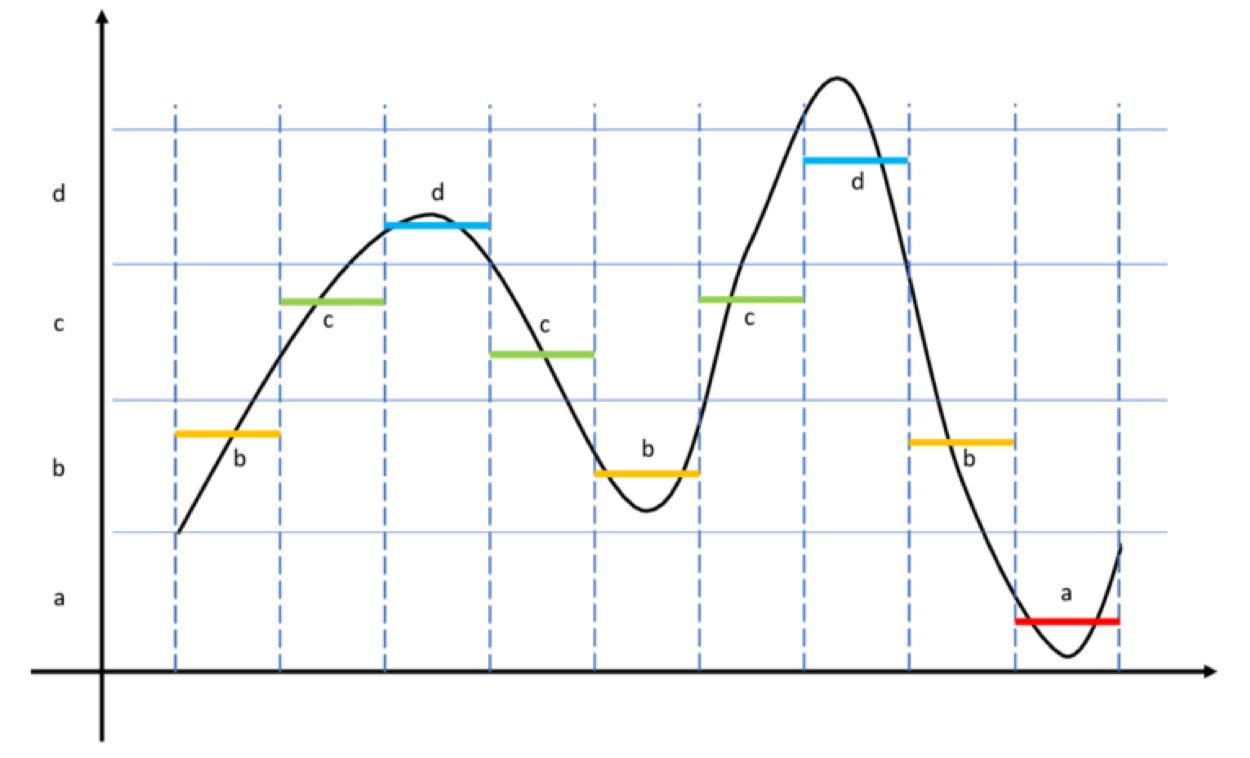
Quantitative Measures
Ngoài việc quan sát trực quan, chuỗi thời gian còn có thể được định lượng các đặc trưng chính: xu hướng (trend), mùa vụ (seasonality), và phần dư (remainder). Các công thức này giúp đo lường mức độ mạnh/yếu của từng thành phần. Original Observations
-
Dữ liệu ban đầu (original data) chứa tổng hợp của trend + seasonality + remainder.
-
Độ phân tán dữ liệu được đo bằng phương sai (variance):
Trong đó:
- xi: giá trị quan sát
- μ: trung bình
- n: số lượng quan sát
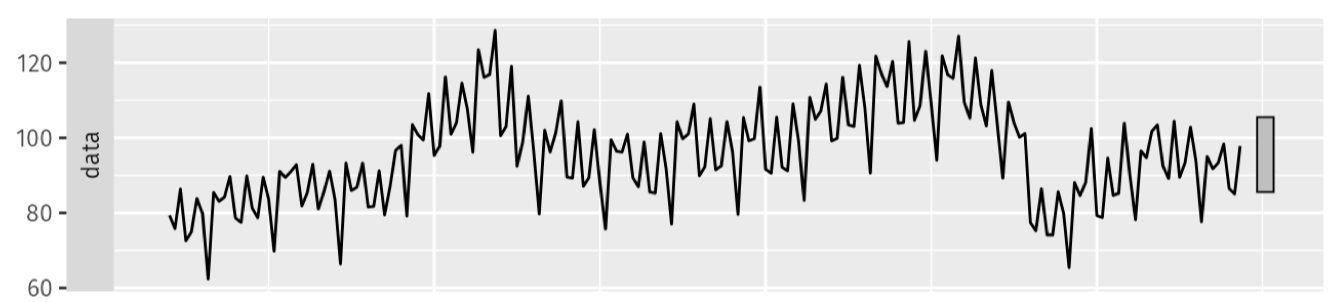 Long-term Direction (Trend Strength)
Long-term Direction (Trend Strength)
-
Xu hướng dài hạn phản ánh sự thay đổi ổn định (tăng hoặc giảm) theo thời gian.
-
Được định lượng bởi công thức:
Trong đó:
- R: phần dư
- S: thành phần mùa vụ
- X: dữ liệu gốc
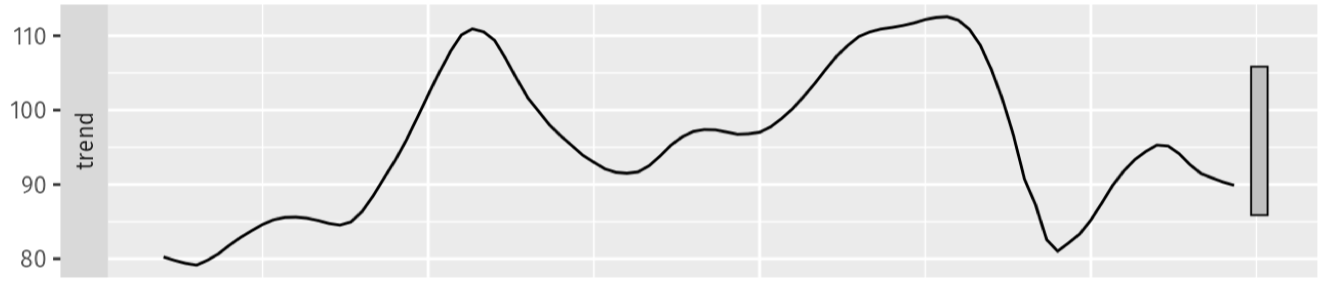 Repeating Patterns (Seasonality Strength)
Repeating Patterns (Seasonality Strength)
-
Tính mùa vụ là các mẫu lặp lại có chu kỳ cố định.
-
Được định lượng bởi công thức:
Trong đó:
- T: thành phần xu hướng
- R: phần dư
- X: dữ liệu gốc
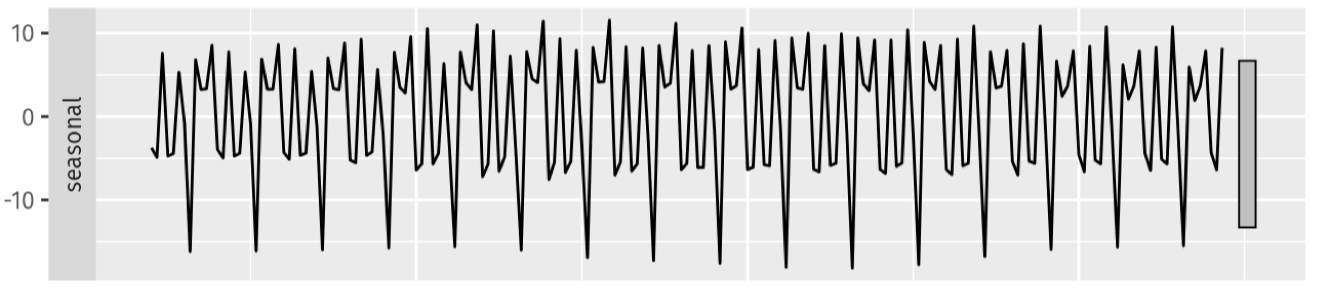 Random Noise (Remainder)
Random Noise (Remainder)
-
Phần dư là biến động không giải thích được sau khi loại bỏ trend và seasonality:
-
Nếu phương sai của remainder lớn → mô hình có thể đang bỏ sót những mẫu quan trọng.
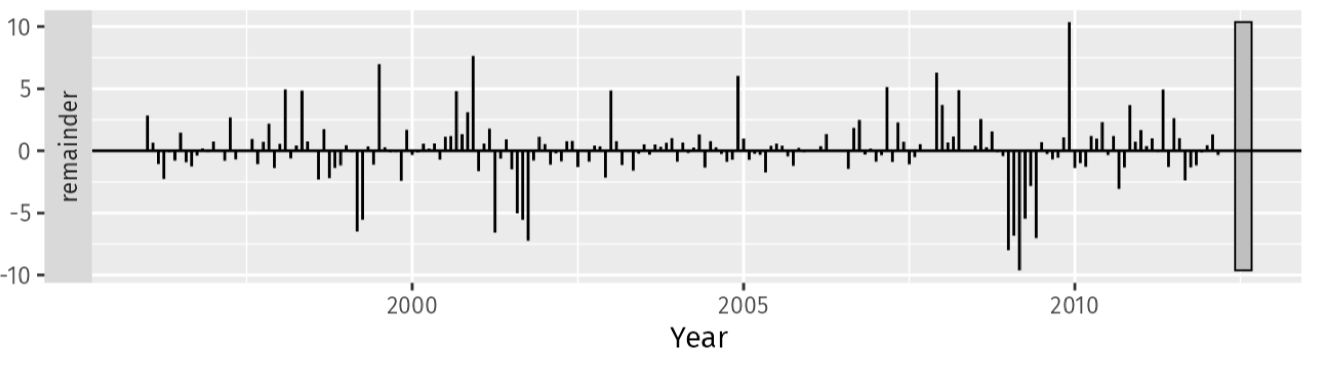
Transition
Transition trong chuỗi thời gian là những đặc trưng cố định, có thể nhận diện rõ ràng, chẳng hạn như sự xuất hiện của trend, chu kỳ (periodicity) hoặc sự kết hợp đồng thời giữa seasonality và trend. Chúng phản ánh sự thay đổi trạng thái (regime changes) của chuỗi.
-
Transition xuất hiện khi dữ liệu di chuyển từ một trạng thái này sang trạng thái khác.
-
Có thể là chuyển mức, chuyển pha, hoặc thay đổi chế độ vận hành trong dữ liệu.
-
Ví dụ: giá cổ phiếu chuyển từ pha tăng trưởng sang pha giảm, hoặc cảm biến hoạt động trong nhiều chế độ khác nhau.
 Công thức định lượng Transition:
Thuật toán giúp tính toán giá trị Transition Value (Δ) từ chuỗi thời gian X.
Công thức định lượng Transition:
Thuật toán giúp tính toán giá trị Transition Value (Δ) từ chuỗi thời gian X. -
Input: chuỗi thời gian
-
Output: giá trị
 Các bước chính:
Các bước chính:
-
Tìm điểm zero-crossing đầu tiên của hàm tự tương quan (autocorrelation).
-
Giảm mẫu chuỗi theo bước τ.
-
Sinh vector đặc trưng Z.
-
Xây dựng ma trận chuyển trạng thái M ∈ ℝ^(3×3).
-
Chuẩn hóa M → M′.
-
Tính ma trận hiệp phương sai C giữa các cột của M′.
-
Tính giá trị transition:
Trong đó C là ma trận hiệp phương sai của xác suất chuyển trạng thái.
Ý nghĩa của Transition:
- Phát hiện thay đổi chế độ (regime changes) trong chuỗi thời gian.
- Phát hiện bất thường (anomaly detection).
- Phân biệt hành vi khác nhau của các chuỗi thời gian.
4. Model
4.1. By IO Shape and IO Type
Khi xây dựng mô hình dự báo chuỗi thời gian, một cách phân loại quan trọng là dựa trên Input–Output (IO) Shape và IO Type. Cách phân loại này quyết định cách mô hình xử lý dữ liệu lịch sử và sinh ra dự báo.
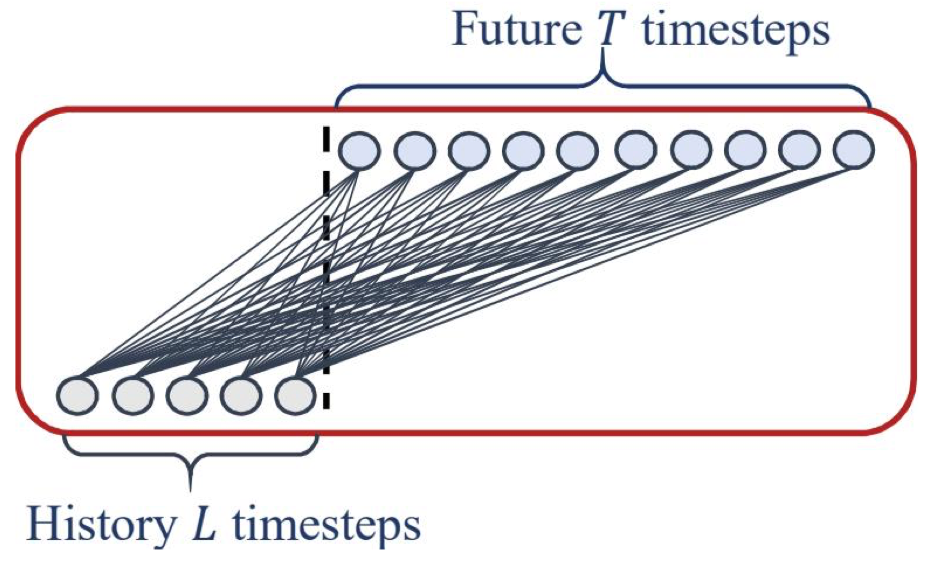
By IO Shape
- Short-term
- Sử dụng một số lượng nhỏ bước thời gian cho cả đầu vào và đầu ra.
- Độ dài đầu ra ≤ độ dài đầu vào.
- Thường phù hợp với dự báo ngắn hạn hoặc trong phạm vi một chu kỳ nhỏ.
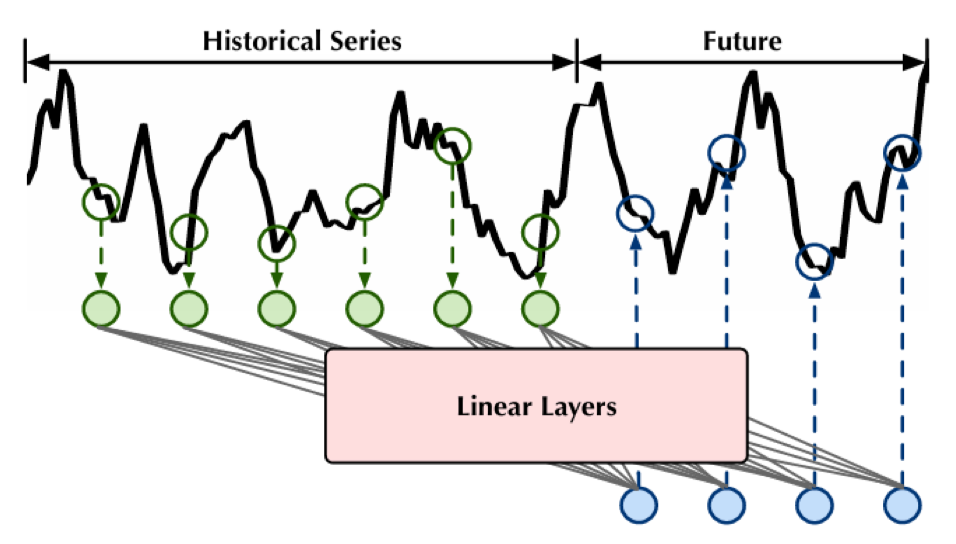
- Long-term
- Sử dụng số lượng lớn bước thời gian cho cả đầu vào và đầu ra.
- Độ dài đầu ra ≥ độ dài đầu vào.
- Dùng cho dự báo dài hạn, có tính chu kỳ hoặc xu hướng mạnh.
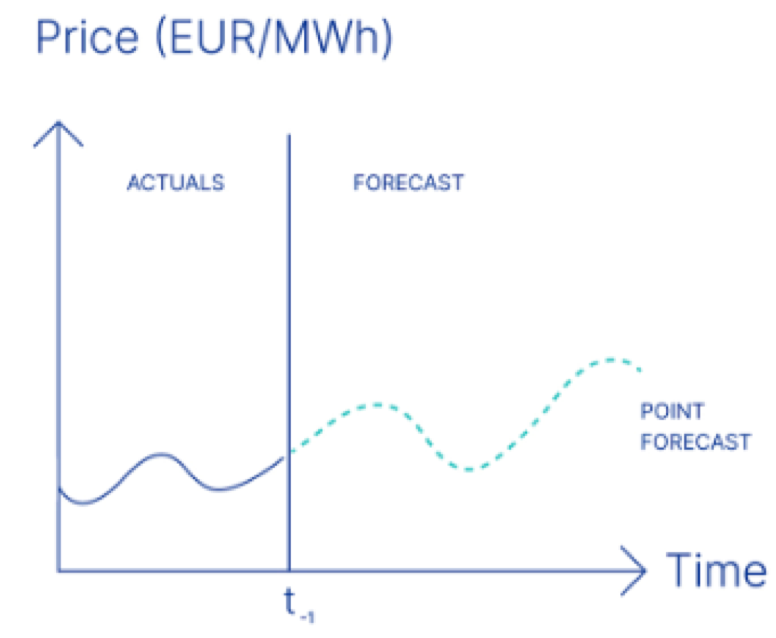
By IO Type
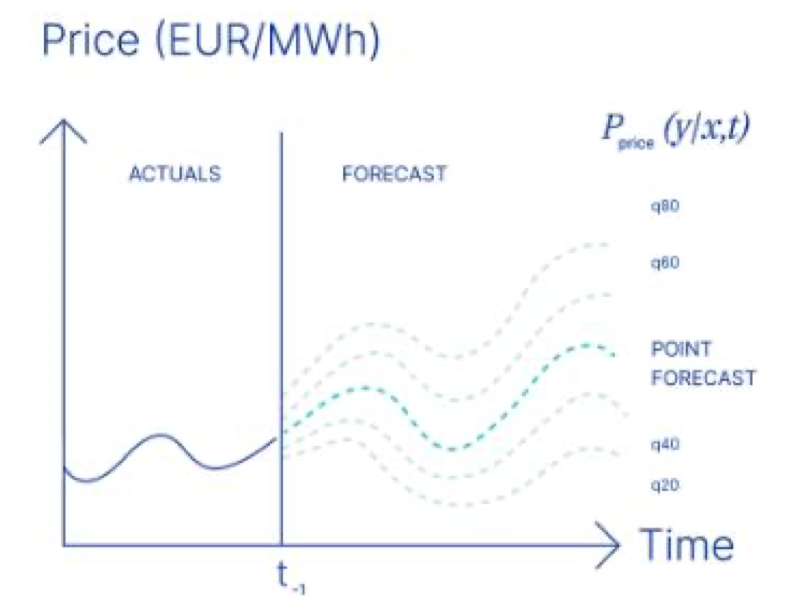
- Point / Deterministic
- Đầu ra của mô hình là giá trị chính xác duy nhất cho mỗi bước thời gian trong tương lai.
- Dùng khi dữ liệu có ít nhiễu hoặc khi cần giá trị cụ thể để ra quyết định.
- Probabilistic
- Đầu ra là một khoảng giá trị (upper bound và lower bound) hoặc phân phối xác suất.
- Thể hiện độ không chắc chắn trong dự báo.
- Hữu ích khi dữ liệu có nhiễu hoặc cần đánh giá rủi ro.
4.2. By Method
Một cách phân loại mô hình dự báo chuỗi thời gian là dựa trên phương pháp dự báo. Hai cách tiếp cận phổ biến là Direct và Recursive.
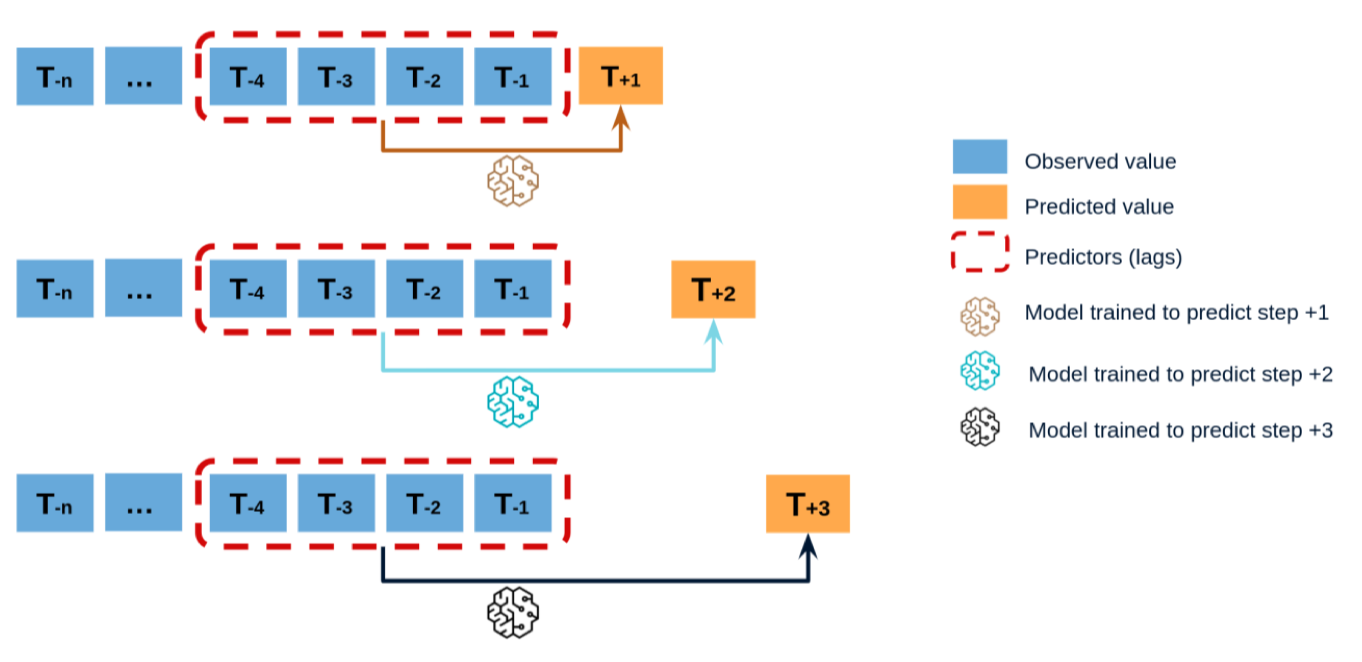
Direct Method
- Cách hoạt động: Mô hình được huấn luyện để dự báo trực tiếp số bước thời gian tương lai theo yêu cầu.
- Đặc điểm:
- Mỗi điểm tương lai được dự báo bởi một mô hình riêng hoặc một mạng nhiều đầu ra.
- Giảm sự tích lũy sai số, vì không phụ thuộc vào dự báo trước đó.
- Ví dụ: Dự báo trực tiếp T+1, T+2, T+3 từ dữ liệu quá khứ T−n…T−1.
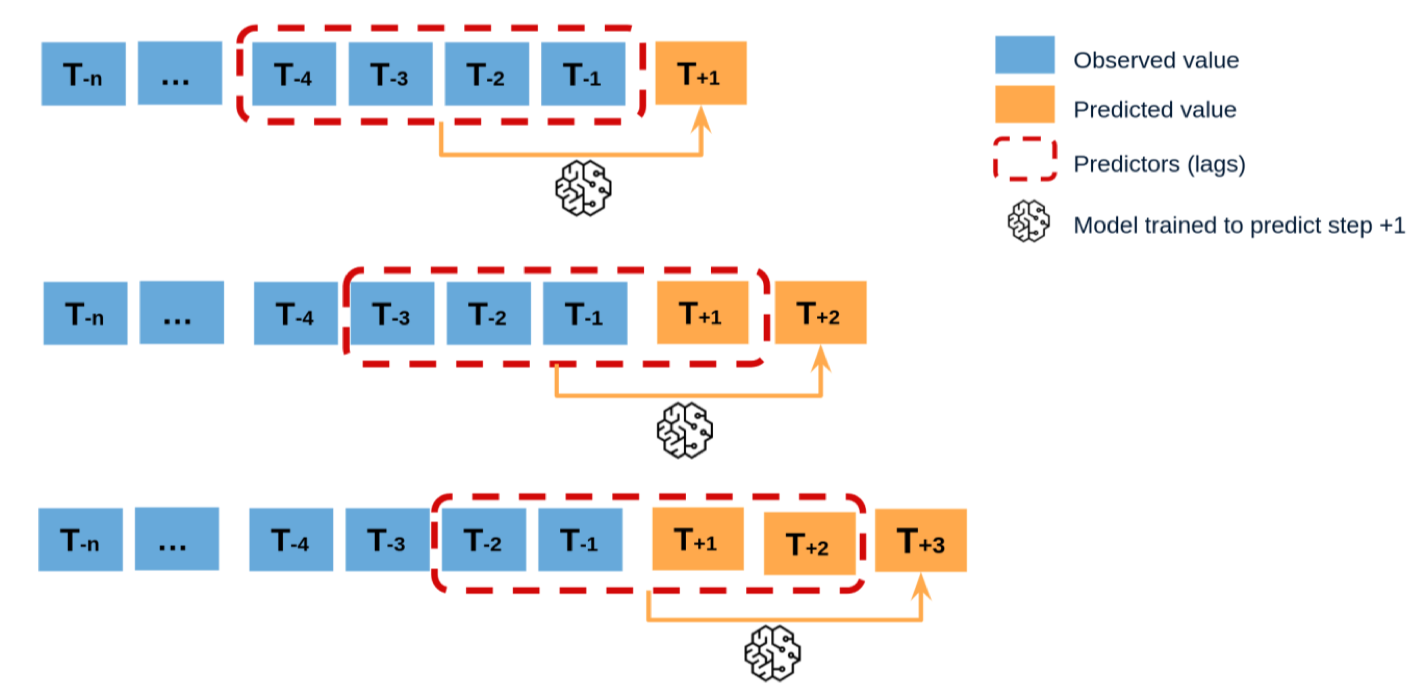
Recursive Method
- Cách hoạt động: Mô hình dự báo từng bước một. Dự báo ở bước trước sẽ được dùng làm đầu vào để dự báo bước tiếp theo.
- Đặc điểm:
- Chỉ cần một mô hình cho tất cả các bước.
- Nhược điểm: sai số tích lũy theo thời gian, vì mỗi dự báo phụ thuộc vào giá trị dự báo trước đó.
- Ví dụ: Từ dữ liệu quá khứ T−n…T−1, mô hình dự báo T+1; sau đó dùng cả T+1 để dự báo T+2; rồi tiếp tục đến T+3.
4.3. By Architecture
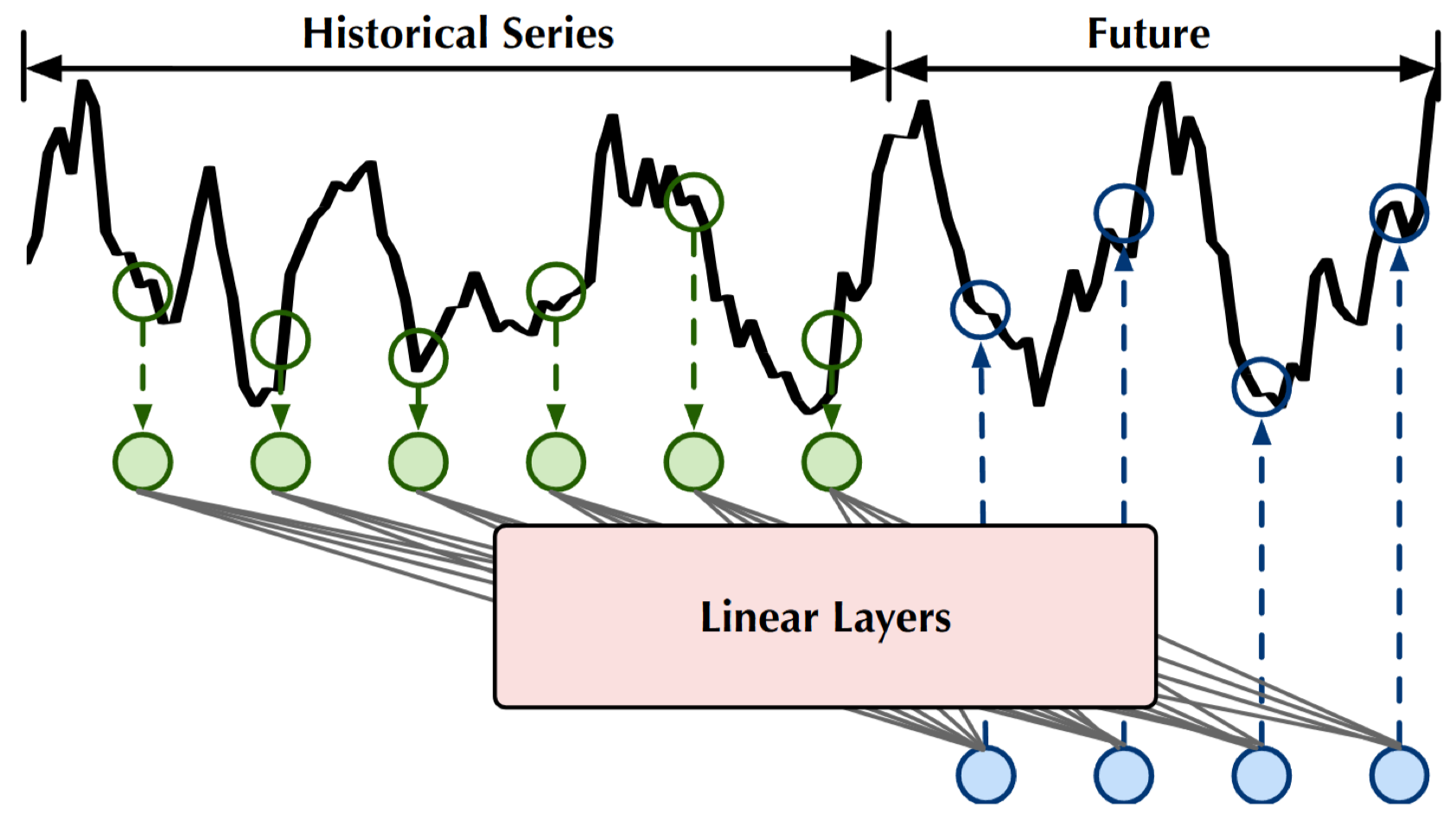
MLP
Một trong những kiến trúc cơ bản để dự báo chuỗi thời gian là MLP (Multi-Layer Perceptron). Đây là mô hình mạng nơ-ron truyền thẳng (feed-forward neural network), có thể áp dụng trực tiếp cho dữ liệu chuỗi sau khi được biến đổi thành các vector đầu vào/đầu ra.
- Ưu điểm:
- Cấu trúc rất đơn giản và huấn luyện nhanh.
- Phù hợp để thử nghiệm ban đầu với dữ liệu chuỗi thời gian.
- Nhược điểm:
- Không có trí nhớ về dữ liệu trong quá khứ.
- Không hiểu rõ thứ tự thời gian của các điểm dữ liệu.
 Các biến thể của MLP cho Time Series:
Các biến thể của MLP cho Time Series:
- Linear: chỉ có 1 tầng tuyến tính.
- NLinear: 1 tầng tuyến tính + chuẩn hóa (normalization).
- DLinear: 1 tầng tuyến tính + decomposition.
- N-BEATS: mô hình thuần MLP, không dùng kiến thức đặc thù chuỗi thời gian, nhưng hiệu quả nhờ nhiều tầng chồng lên nhau.
- FITS: linear layer được chỉnh sửa, có khả năng học biến đổi biên độ và dịch pha.
- TSMixer: kết hợp MLP với Mixer.
- TimeMixer: MLP + đa tỉ lệ (multi-scale) + decomposition + Mixer. Khi nào dùng MLP
- Khi cần baseline model đơn giản để so sánh với các mô hình khác.
- Khi chuỗi thời gian đã được tiền xử lý tốt (ví dụ decomposition, feature engineering).
- Khi cần tốc độ huấn luyện nhanh để thử nghiệm nhiều kịch bản.
RNN
RNN (Recurrent Neural Network) là một kiến trúc phổ biến cho chuỗi thời gian, có khả năng ghi nhớ và khai thác thông tin tuần tự nhờ cơ chế hồi tiếp (recurrent connections). Đặc điểm:
- Ưu điểm:
- Có bộ nhớ để hiểu và xử lý dữ liệu tuần tự.
- Có thể làm việc với chuỗi có độ dài khác nhau.
- Phù hợp với dữ liệu có tính phụ thuộc theo thời gian.
- Nhược điểm:
- Huấn luyện chậm, khó song song hóa.
- Dễ gặp vấn đề quên thông tin xa (vanishing gradient).
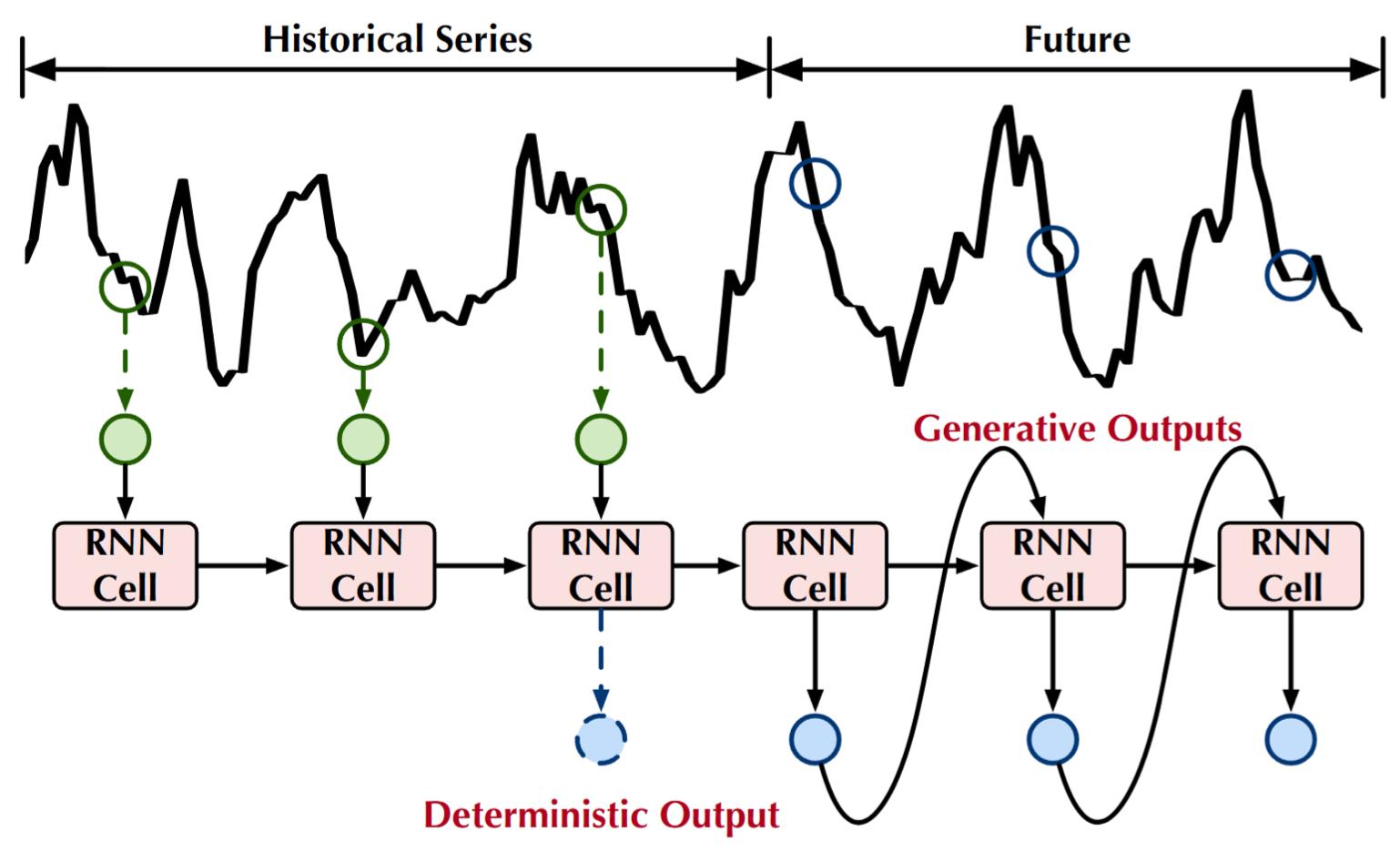 Các biến thể của RNN cho Time Series
Các biến thể của RNN cho Time Series
- LSTNet: kết hợp convolution (bắt đặc trưng ngắn hạn) + LSTM/GRU (bắt đặc trưng dài hạn).
- DA-RNN: RNN + Dual Attention, gán trọng số cao hơn cho các biến đặc trưng quan trọng.
- SegRNN: RNN/LSTM/GRU + segment-wise iteration để giảm số vòng lặp hồi quy + Parallel Multi-step Forecasting.
- xLSTM: kết hợp sLSTM (memory mixing mới) + mLSTM (matrix memory, cập nhật theo covariance rule), có khả năng song song hóa.
- xLSTMTime: decomposition + xLSTM + normalization. Khi nào dùng RNN
- Khi dữ liệu có chuỗi dài hạn nhưng không quá phức tạp.
- Khi cần mô hình có thể học từ phụ thuộc thời gian mà MLP không xử lý được.
- Khi muốn kết hợp với attention hoặc convolution để tăng hiệu quả.
CNN
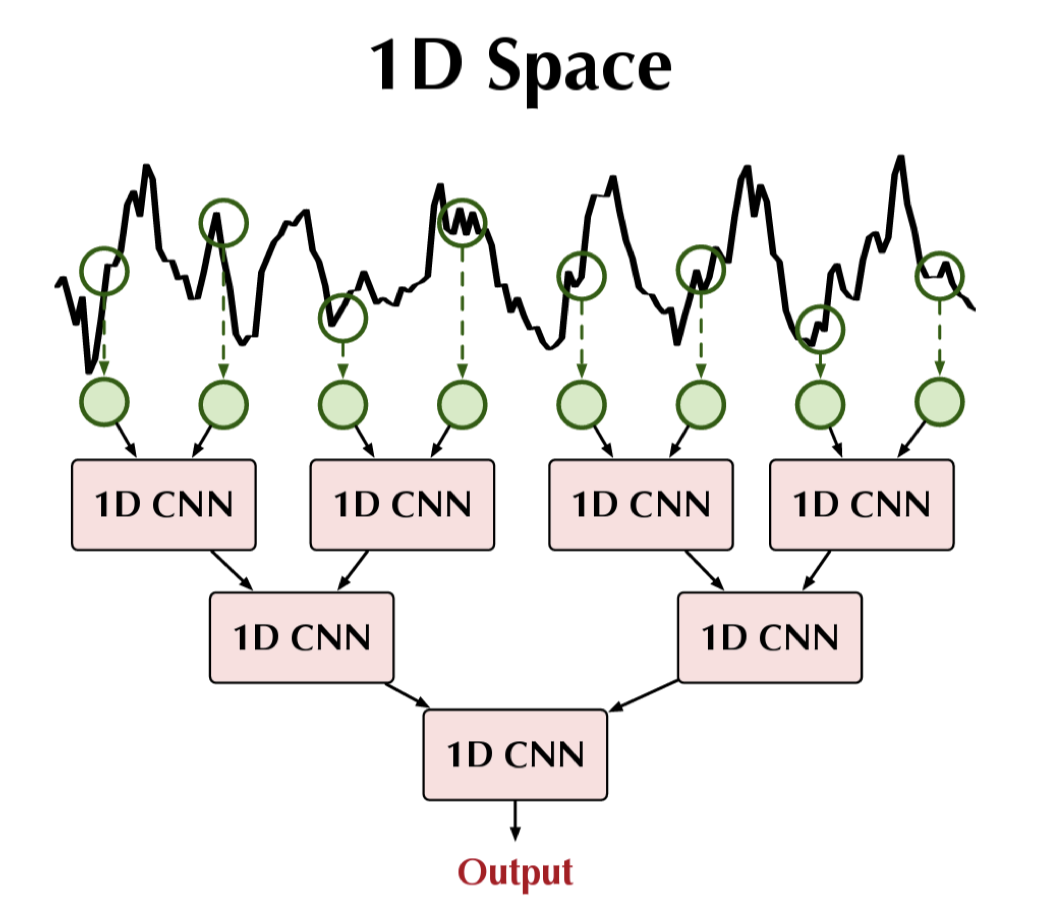
CNN (Convolutional Neural Network) thường được biết đến trong xử lý ảnh, nhưng cũng được ứng dụng mạnh mẽ trong chuỗi thời gian. CNN đặc biệt hiệu quả trong việc phát hiện các mẫu cục bộ (local patterns) xuất hiện trong khoảng thời gian ngắn. CNN trong không gian 1D:
- Cách hoạt động: áp dụng convolution trực tiếp trên chuỗi 1D.
- Ưu điểm:
- Phát hiện tốt các mẫu lặp ngắn hạn (motifs).
- Học được quan hệ cục bộ theo thời gian gần.
- Hạn chế: khó nắm bắt quan hệ dài hạn.
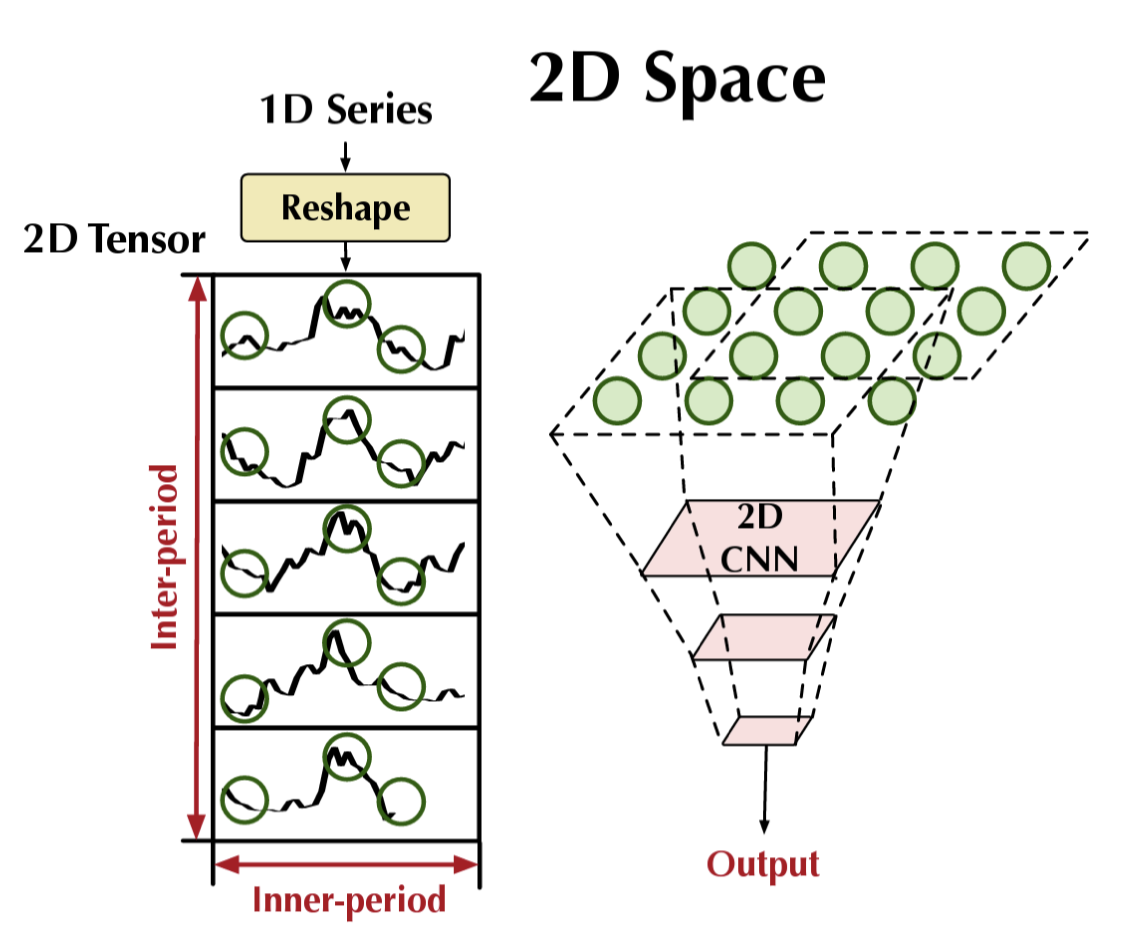
 CNN trong không gian 2D
CNN trong không gian 2D
- Cách hoạt động: chuỗi 1D được reshape thành tensor 2D (theo inner-period và inter-period), sau đó áp dụng 2D convolution.
- Ưu điểm:
- Phát hiện cấu trúc lặp trong một chu kỳ (inner-period).
- Đồng thời học được mối quan hệ giữa các chu kỳ khác nhau (inter-period).
- Ứng dụng: hữu ích với dữ liệu có chu kỳ phức tạp (ví dụ: nhu cầu năng lượng, chu kỳ kinh tế).
 Khi nào dùng CNN?
Khi nào dùng CNN? - Khi dữ liệu có mẫu cục bộ rõ ràng (ví dụ: sóng điện tim ECG, chu kỳ bán hàng ngắn hạn).
- Khi muốn tăng tốc huấn luyện (CNN thường song song hóa tốt hơn RNN).
- Khi dữ liệu có chu kỳ lặp lại phức tạp → dùng 2D CNN để khai thác cả inner và inter-period.
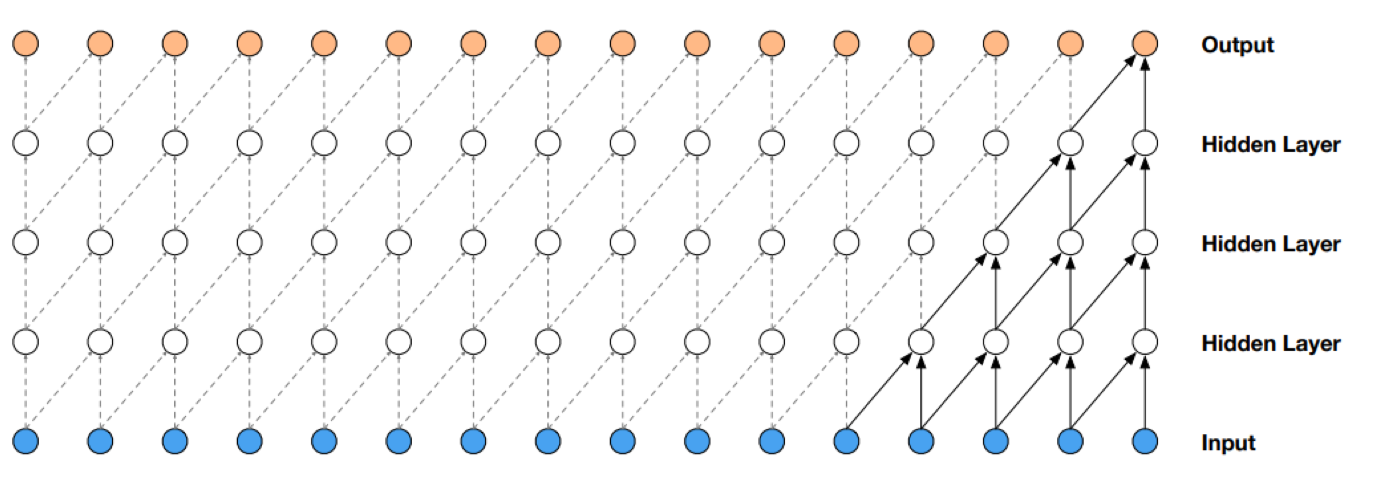
TCN
Temporal Convolutional Networks (TCN) là một dạng CNN chuyên biệt cho chuỗi thời gian. Khác với RNN, TCN sử dụng convolution nhân quả (causal convolution) để đảm bảo không có “leakage” từ tương lai, đồng thời mở rộng khả năng quan sát quá khứ bằng dilated convolution. Đặc điểm chính:
- Causality: chỉ sử dụng thông tin từ quá khứ để dự đoán → không rò rỉ thông tin tương lai.
- Dilations: mở rộng receptive field theo cấp số nhân, cho phép nắm bắt quan hệ dài hạn mà vẫn giữ chi phí tính toán hợp lý.
- Residual connections: giúp huấn luyện ổn định hơn, tránh gradient vanish.
- Fully convolutional: xử lý hiệu quả chuỗi dài nhờ hoàn toàn dựa trên convolution thay vì tính tuần tự.
- Ưu điểm
- Song song hóa tốt hơn RNN, huấn luyện nhanh.
- Nắm bắt được cả đặc trưng ngắn hạn và dài hạn nhờ dilated convolution.
- Cấu trúc đơn giản, dễ mở rộng.
- Nhược điểm
- Thiếu cơ chế chú ý (attention), nên với chuỗi có phụ thuộc phức tạp, có thể kém hiệu quả hơn Transformer.
- Độ linh hoạt thấp hơn RNN/LSTM khi dữ liệu có tính phi tuyến cao. Ứng dụng
- Dự báo nhu cầu (demand forecasting).
- Nhận dạng tín hiệu (speech recognition).
- Phân tích chuỗi cảm biến IoT.
- Mô hình nổi tiếng: Wavenet (Google DeepMind), sử dụng causal + dilated convolution cho xử lý âm thanh.
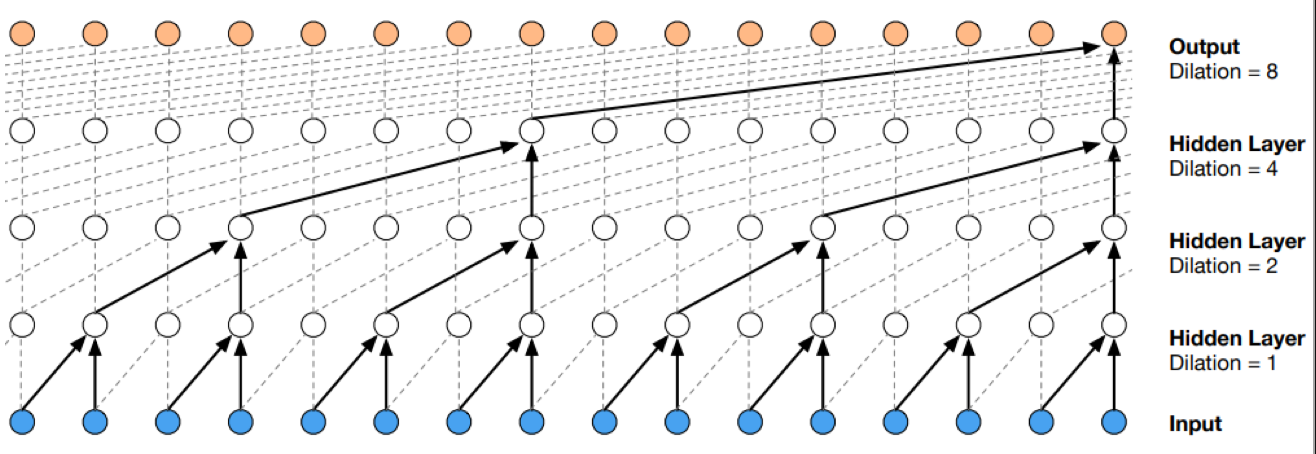 Visualization of a stack of dilated causal convolutional layers.
Tại sao phải dilate (giãn, mở rộng) như vậy?
→ Để tăng độ dài thời gian cho dữ liệu đầu vào, giữ lại được khung thời gian dài hơn, nhiều thông tin seasonal
Visualization of a stack of dilated causal convolutional layers.
Tại sao phải dilate (giãn, mở rộng) như vậy?
→ Để tăng độ dài thời gian cho dữ liệu đầu vào, giữ lại được khung thời gian dài hơn, nhiều thông tin seasonal