M05W1.4. A Bridge to Linear Regression

1. Optimization

1.1. Đạo hàm cho hàm liên tục

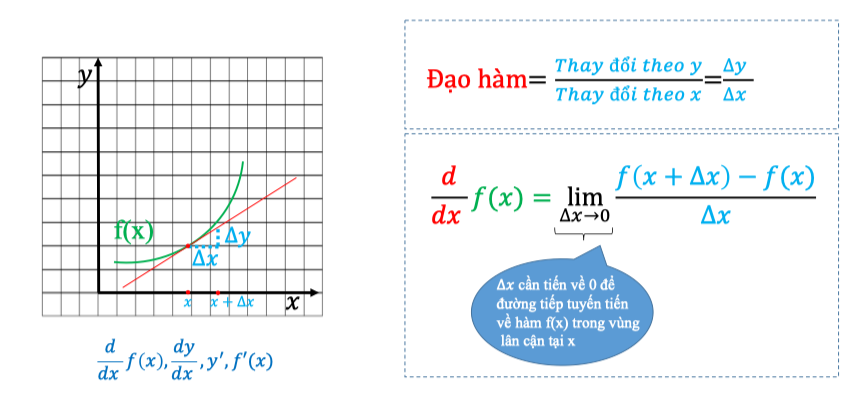
Trong phép chia $\frac{a}{b}$, điều kiện tiên quyết là $b\ne 0$. Do đó, trong công thức đạo hàm, $\Delta x$ cũng không được bằng 0. Nếu xét một hàm số không liên tục (bị gián đoạn) thì tại điểm gãy, giá trị $\Delta x$ tiến về 0 không còn ý nghĩa. Chính vì vậy, tại điểm không liên tục ta không thể xác định được đạo hàm của hàm số.

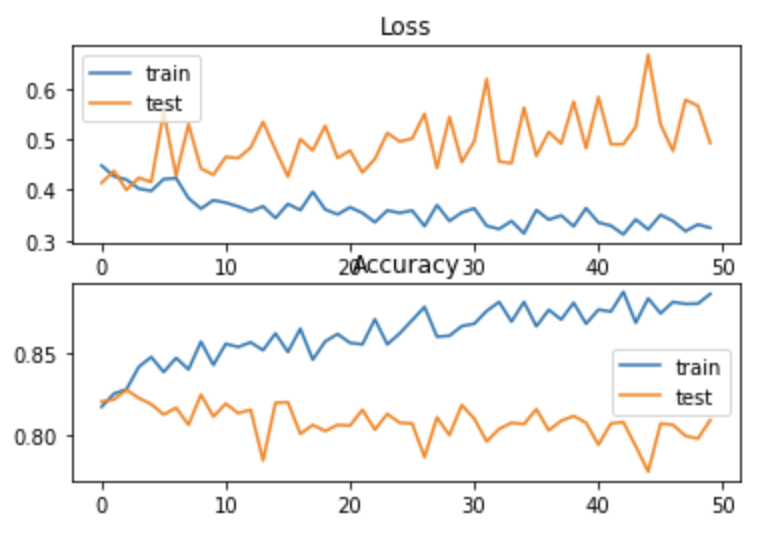
Ví dụ ở đây ta thấy hàm Accuracy bị đứt gãy vì thế đây là hàm không liên tục.

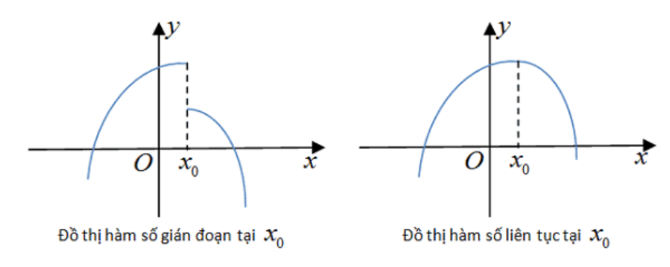
1.1.1. Hàm liên tục

Một hàm số $f(x)$ được gọi là liên tục (khả vi) tại điểm $x=a$ nếu thỏa các điều kiện sau:

1. $f(a)$ xác định (tức là tại $x=a$ hàm có giá trị cụ thể).
2. Giới hạn ${\lim }_{x\to a}f(x)$ tồn tại.
3. Giá trị của hàm tại điểm bằng giới hạn: ${\lim }_{x\to a}f(x)=f(a)$ Nếu thỏa cả ba điều kiện trên tại mọi điểm trong miền xác định thì ta nói hàm số đó liên tục trên miền đó.

---

1.1.2. Cách xác định cực trị

Điều kiện cần (dùng đạo hàm bậc 1)

• Cho hàm số $y=f(x)$ xác định trên khoảng $D$.
• Tính đạo hàm $f^{\prime }(x)$.
• Tìm điểm tới hạn (critical points): nghiệm của $f^{\prime }(x)=0$ hoặc những điểm mà $f^{\prime }(x)$ không xác định nhưng $f(x)$ xác định.

Điều kiện đủ Có 2 cách thường dùng: (a) Dùng dấu của đạo hàm bậc 1

• Lập bảng biến thiên.
• Nếu $f^{\prime }(x)$ đổi dấu từ dương sang âm tại $x_0$ → $f(x_0)$ là cực đại.
• Nếu $f^{\prime }(x)$ đổi dấu từ âm sang dương tại $x_0$ → $f(x_0)$ là cực tiểu.
• Nếu $f^{\prime }(x)$ không đổi dấu → $x_0$ không phải cực trị. (b) Dùng đạo hàm bậc 2
• Nếu $f^{\prime }(x_0)=0$ và:
  • $f^{\prime \prime }(x_0)>0$ → $f(x_0)$ là cực tiểu.
  • $f^{\prime \prime }(x_0)<0$ → $f(x_0)$ là cực đại.
  • $f^{\prime \prime }(x_0)=0$ → chưa kết luận, phải quay lại cách (a).

Kết luận cực trị

• Giá trị cực trị là $f(x_0)$.
• Điểm cực trị là $(x_0,f(x_0))$.

---

Ví dụ

Xét $f(x)=(x-2{)}^2+1$.

1. Tính đạo hàm: $f^{\prime }(x)=2(x-2)$ → nghiệm: $x=2$.
2. Dùng đạo hàm bậc 2: $f^{\prime \prime }(x)=2$
   • $f^{\prime \prime }(2)=2>0$ → cực tiểu tại $x=2$, giá trị $f(2)=1$. → Hàm có cực tiểu $(2,1)$.