7. XAI - Giải thuật SHAP

1. Shapley Value

Trả lời câu hỏi: “Mỗi thành phần đóng góp bao nhiêu vào kết quả tổng thể?”

• Ý tưởng: So sánh kết quả khi có và không có thành phần đó.
• Shapley Value = Trung bình các đóng góp biên (marginal contributions) trên tất cả hoán vị của các feature.

Ví dụ

Giả sử có 2 người chơi (Player 1 và Player 2) cùng tham gia cuộc thi AI trên Kaggle.
Giải thưởng được trao cho:

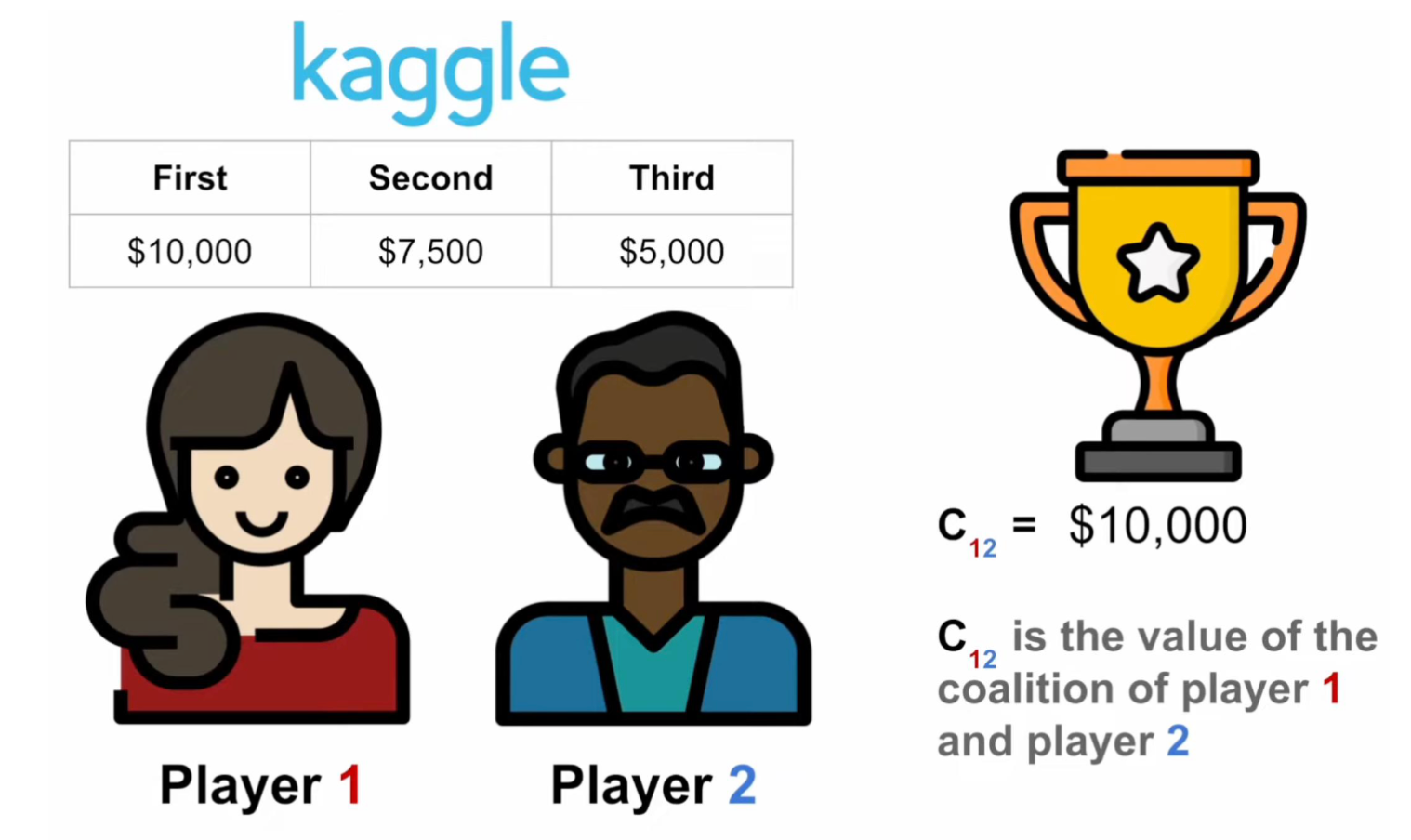
Hạng	Phần thưởng
1 st	$10 000
2 nd	$7 500
3 rd	$5 000

Nếu cả hai cùng hợp tác, họ đoạt **hạng nhất → $10000\ast \ast .\to K\acute{y}hiệu:$C_{12} = 10 000$

Vấn đề đặt ra Làm sao chia $10 000 công bằng giữa hai người?

• Player 1 đóng góp phần lớn phần cứng (GPU NVIDIA H 200 141 GB SXM).
• Player 2 viết mã huấn luyện và tối ưu mô hình.

Cả hai cùng tạo nên chiến thắng.
Ta cần một cách chia thưởng phản ánh đúng đóng góp của từng người.

Bước 1: Xác định giá trị của từng nhóm (coalition values)

Tổ hợp người chơi	Ký hiệu	Giá trị (phần thưởng)
Không ai tham gia	$C_0$	0
Chỉ Player 1	$C_1$	7 500
Chỉ Player 2	$C_2$	5 000
Cả hai cùng chơi	$C_{12}$	10 000

Đây là bảng coalition values – biểu thị giá trị mỗi nhóm đạt được.

Bước 2: Tính đóng góp biên (marginal contribution) Đóng góp biên = phần giá trị tăng thêm khi người chơi tham gia vào nhóm.

• Với Player 1:
  • Khi vào nhóm 2 → $C_{12}-C_2=5000$
  • Khi tham gia từ đầu (vào nhóm trống) → $C_1-C_0=7500$
    → Trung bình: $(5000+7500)/2=6250$
• Với Player 2:
  • Khi vào nhóm 1 → $C_{12}-C_1=2500$
  • Khi tham gia từ đầu → $C_2-C_0=5000$
    → Trung bình: $(2500+5000)/2=3750$

Kết quả:

Người chơi	Đóng góp biên trung bình	Tỷ lệ chia
Player 1	$6 250	62.5 %
Player 2	$3 750	37.5 %

Đây là Shapley Value cho 2 người.
Tổng vẫn đúng: $6250+3750=10000$.

---

Bước 3: Tổng quát công thức Shapley Value

Với $n$ người chơi: ${\varphi }_i={\sum }_{S\subseteq N\setminus \{i\}}\frac{|S|!(n-|S|-1)!}{n!}[v(S\cup \{i\})-v(S)]$

• $v(S)$: giá trị của tập con $S$.
• $[v(S\cup i)-v(S)]$: đóng góp biên của người chơi i khi tham gia vào S.
• Hệ số $\frac{|S|!(n-|S|-1)!}{n!}$: trọng số xác suất cho mọi thứ tự tham gia có thể.

Bước 4: Ví dụ với 3 người chơi Khi thêm Player 3 vào, ta có: Để tính trung bình đóng góp biên của player 1, đầu tiên ta tính xác suất cho các trường hợp (trọng số để tính trung bình)

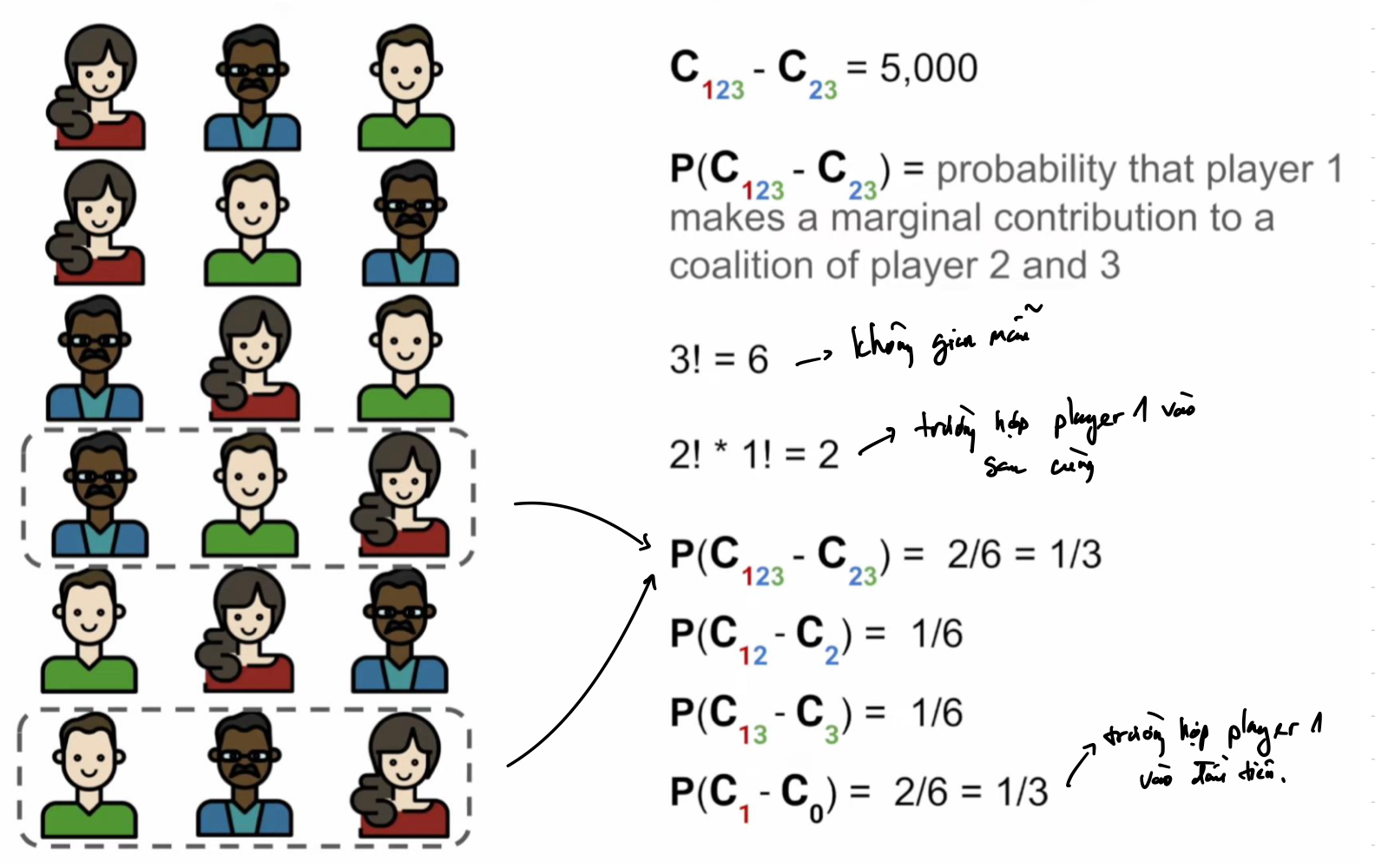
Từ đó ta có thể tính được trung bình đóng góp biên của player1

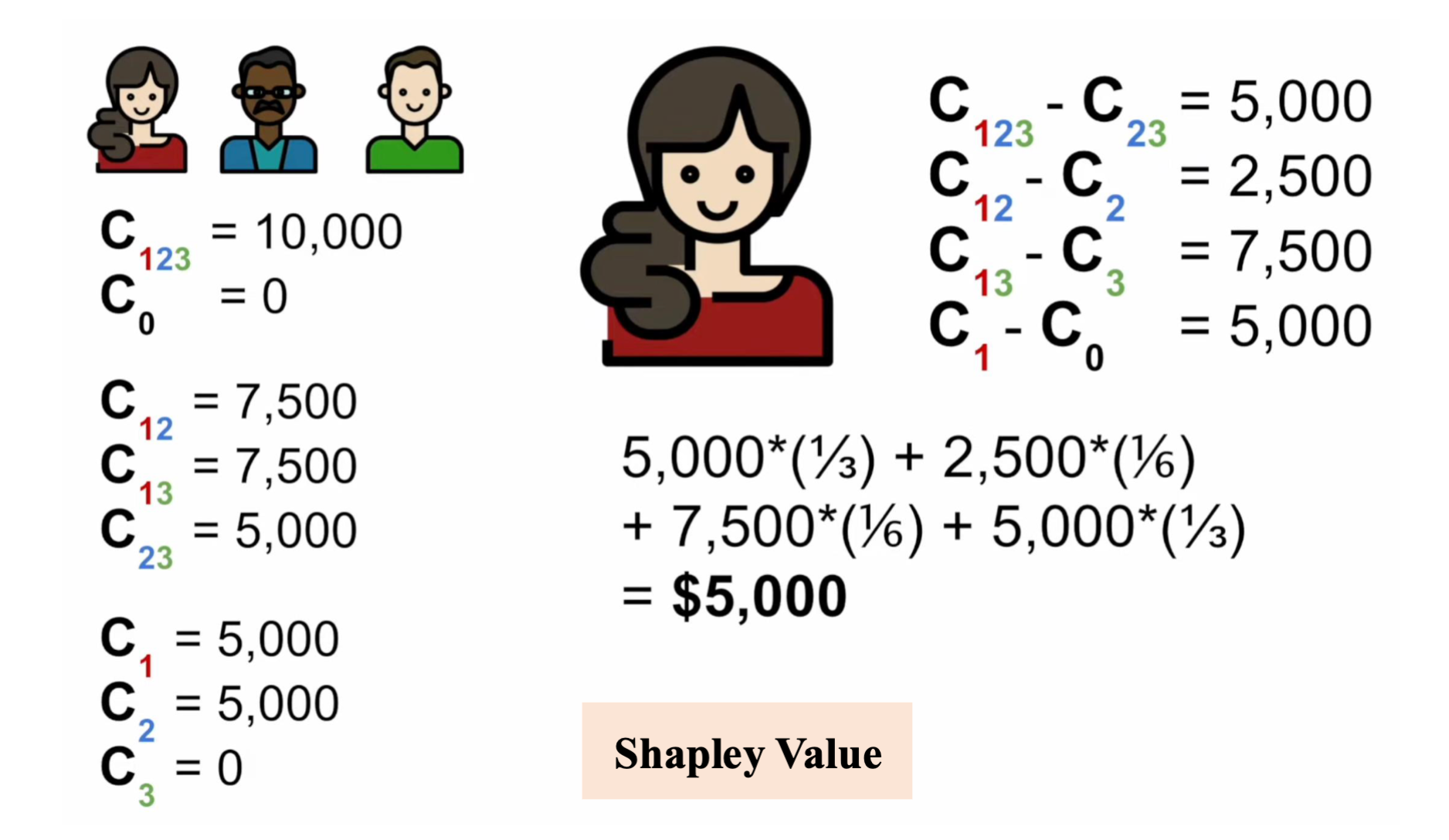
Kết luận Shapley Value = Expected Marginal Contribution
→ Là trung bình có trọng số của mọi đóng góp biên có thể xảy ra. Ưu điểm:

• Công bằng: mọi người được chia đúng với mức ảnh hưởng của mình.
• Dễ mở rộng cho nhiều người (hoặc nhiều feature trong mô hình ML).

Ứng dụng trong XAI Trong mô hình ML:

• “Người chơi” = các feature.
• “Giá trị (reward)” = mức dự đoán của mô hình.
• “Đóng góp biên” = mức thay đổi dự đoán khi thêm feature đó.

→ SHAP (SHapley Additive exPlanations) sử dụng nguyên lý này để đo lường tầm quan trọng của từng feature trong một dự đoán cụ thể.

---

Shapley Value for ML

$$f(x)-{\mathbb{E}}_X[f(X)]=\sum _i{\varphi }_i$$

Hoặc tương đương

$$f(x)={\mathbb{E}}_X[f(X)]+\sum _{i=1}^p{\varphi }_i$$

Ký hiệu	Ý nghĩa
$f(x)$	Kết quả dự đoán của mô hình cho mẫu cần giải thích
${\mathbb{E}}_X[f(X)]$	Giá trị trung bình của mô hình (base value) – dự đoán trung bình nếu không biết gì về dữ liệu
${\varphi }_i$	Đóng góp của feature thứ i vào việc đẩy kết quả từ base value lên (hoặc xuống) $f(x)$

Nói cách khác:

“Dự đoán của mô hình = Giá trị nền + Tổng đóng góp của từng feature.”

Ví dụ:

• Trung bình mô hình dự đoán 0.3 xác suất được duyệt vay.
• Với khách hàng A, mô hình cho 0.55.
• Các đóng góp là:
  • Tuổi: +0.10
  • Thu nhập: +0.20
  • Nợ xấu: −0.05 → $0.55=0.3+(0.10+0.20-0.05)$

Bốn thuộc tính (axioms) đảm bảo tính “công bằng” của Shapley Value

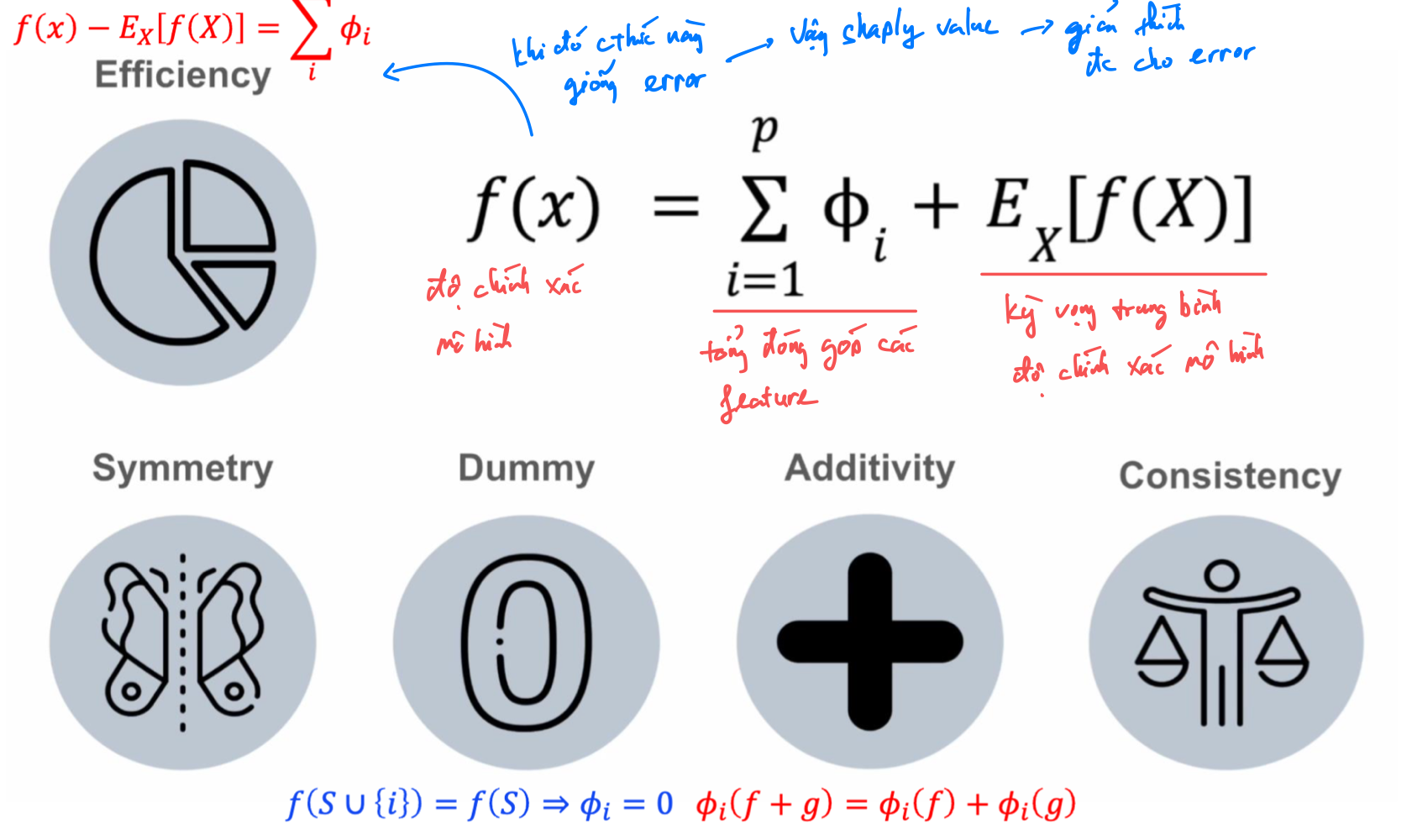
Shapley chứng minh rằng chỉ có một cách chia duy nhất thỏa mãn 4 tiêu chí công bằng này — đó chính là Shapley Value.

(1) Efficiency – Hiệu quả ${\sum }_i{\varphi }_i=f(x)-{\mathbb{E}}_X[f(X)]$

→ Tổng đóng góp của tất cả feature phải đúng bằng chênh lệch dự đoán thật so với giá trị trung bình. Ví dụ: mô hình dự đoán cao hơn trung bình 0.25 → tổng tất cả ${\varphi }_i=0.25$.

(2) Symmetry – Tính đối xứng Nếu hai feature đóng góp như nhau cho mọi tình huống, chúng phải nhận giá trị Shapley bằng nhau.

$\text{Neˆˊu }f(S\cup \{i\})-f(S)=f(S\cup \{j\})-f(S)\Rightarrow {\varphi }_i={\varphi }_j$

→ Ví dụ: “diện tích nhà” và “số tầng” có ảnh hưởng tương đương đến giá dự đoán → SHAP phải cho hai feature này cùng giá trị.

(3) Dummy (Null player) – Người chơi không đóng góp Nếu thêm feature i không làm thay đổi kết quả mô hình, thì đóng góp của nó phải bằng 0.

$f(S\cup \{i\})=f(S)\Rightarrow {\varphi }_i=0$

→ Ví dụ: “Mã khách hàng” không ảnh hưởng gì đến dự đoán tín dụng → giá trị SHAP của nó = 0.

(4) Additivity – Tính cộng gộp

Nếu ta có hai mô hình $f$ và $g$, thì SHAP của mô hình tổng $(f+g)$ bằng tổng SHAP của từng mô hình riêng.

${\varphi }_i(f+g)={\varphi }_i(f)+{\varphi }_i(g)$

→ Điều này giúp ta có thể cộng các phần giải thích từ nhiều mô hình hoặc tầng mạng khác nhau.

(5) Consistency – Tính nhất quán Nếu trong một mô hình mới, feature i có đóng góp mạnh hơn (hoặc ít hơn) so với trước, thì giá trị Shapley của nó phải thay đổi cùng hướng.

$\text{Neˆˊu }{f}^{\prime }(S\cup \{i\})-f^{\prime }(S)\ge f(S\cup \{i\})-f(S)\Rightarrow {\varphi }_i(f^{\prime })\ge {\varphi }_i(f)$

→ Tức là khi mô hình “tin tưởng hơn” vào feature i, SHAP phải phản ánh điều đó bằng giá trị lớn hơn.

---

Mức đóng góp (𝜙ᵢ) của feature $i$.

Công thức đóng góp biên:

undefined

\mathbb{E}[f(x)] = \int f(x) P(x) , dx

undefined