Phần này giới thiệu khái niệm độ tương tự (similarity) và độ khác biệt (dissimilarity) trong khai phá dữ liệu.

Trong các ứng dụng như phân cụm (clustering), phát hiện ngoại lệ (outlier detection) và phân loại láng giềng gần nhất (nearest-neighbor classification), việc đo mức độ giống nhau giữa các đối tượng là rất quan trọng.
Mục tiêu là nhóm các đối tượng có đặc điểm tương đồng (ví dụ: thu nhập, khu vực sống, độ tuổi của khách hàng), để tìm ra các cụm (clusters) — mỗi cụm gồm các đối tượng tương tự nhau, và khác biệt với đối tượng ở cụm khác.
Phân tích tương tự cũng giúp xác định ngoại lệ — các đối tượng khác biệt rõ rệt so với phần lớn dữ liệu.
Ngoài ra, độ tương tự còn được dùng trong phân loại dựa trên láng giềng gần nhất (nearest-neighbor classification), khi cần gán nhãn cho một đối tượng mới dựa trên sự giống nhau với các đối tượng đã biết.

Ví dụ minh họa:

Hình 2.21: Đám mây từ khóa (tag cloud) cho thấy các chủ đề phổ biến được gắn thẻ trên web, thể hiện mức độ tương tự giữa các chủ đề theo tần suất xuất hiện.
Hình 2.22: Biểu đồ ảnh hưởng bệnh tật của người trên 20 tuổi (NHANES dataset) cho thấy mối quan hệ giữa các bệnh — những bệnh thường xuất hiện cùng nhau được xem là “tương tự” hơn.

Data Matrix vs. Dissimilarity Matrix

1. Data Matrix (ma trận dữ liệu)

Còn gọi là object-by-attribute structure hoặc two-mode matrix.
Lưu trữ giá trị của các thuộc tính (attributes) cho từng đối tượng (objects).
Có kích thước $n \times p$ , trong đó:
- $n$ : số lượng đối tượng
- $p$ : số thuộc tính (hoặc đặc trưng – features)
Mỗi hàng biểu diễn một đối tượng (object), mỗi cột biểu diễn một thuộc tính.
Ký hiệu:

$x_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i p})$

là vector thuộc tính của đối tượng $i$ .
Ví dụ: tập dữ liệu về khách hàng với các đặc trưng như tuổi, thu nhập, giới tính.

2. Dissimilarity Matrix (ma trận độ khác biệt)

Còn gọi là object-by-object structure hoặc one-mode matrix.
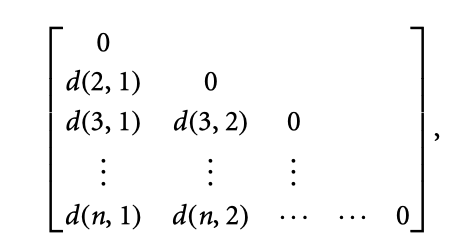
Lưu trữ giá trị đo độ khác biệt (dissimilarity) giữa từng cặp đối tượng $(i, j)$ .
Có kích thước $n \times n$ .
Phần tử $d (i, j)$ biểu diễn mức độ khác biệt giữa hai đối tượng:
- $d (i, j) \geq 0$
- $d (i, i) = 0$
- $d (i, j) = d (j, i)$ (ma trận đối xứng)
Nếu hai đối tượng giống nhau → $d (i, j) = 0$ ; càng khác nhau → giá trị càng lớn.
Dùng trong nhiều thuật toán phân cụm và tìm kiếm tương tự.

3. Mối quan hệ giữa Similarity và Dissimilarity

Hai khái niệm này liên hệ nghịch đảo:

$s im (i, j) = 1 - d (i, j)$

$s im (i, j)$ : độ tương tự giữa hai đối tượng
$d (i, j)$ : độ khác biệt giữa hai đối tượng
$s im (i, j) = 1$ khi hai đối tượng giống hệt nhau; giảm dần khi chúng khác nhau.

Proximity Measures for Nominal Attributes

1. Định nghĩa

Nominal attribute là thuộc tính có các giá trị (state) phân loại rời rạc, không có thứ tự.
→ Ví dụ: map_color có thể có các giá trị {red, yellow, green, pink, blue}.
Số lượng trạng thái của thuộc tính ký hiệu là $M$ . Các giá trị có thể được biểu diễn bằng chữ, ký hiệu, hoặc số nguyên chỉ để xử lý dữ liệu — không biểu thị thứ tự.

2. Đo độ khác biệt (Dissimilarity)

Giữa hai đối tượng $i$ và $j$ có $p$ thuộc tính, ta tính:

$d (i, j) = \frac{p - m}{p}$

$m$ : số lượng thuộc tính mà hai đối tượng giống nhau (match)
$p$ : tổng số thuộc tính mô tả đối tượng

Nói cách khác, dissimilarity = tỷ lệ các thuộc tính khác nhau.
Nếu có trọng số cho từng thuộc tính, có thể điều chỉnh công thức để tăng ảnh hưởng của thuộc tính quan trọng hoặc có nhiều trạng thái hơn.

4. Độ tương tự (Similarity)

Có thể tính tương tự từ công thức nghịch đảo:

$s im (i, j) = 1 - d (i, j) = \frac{m}{p}$

→ Là tỷ lệ các thuộc tính giống nhau.

5. Mã hóa thay thế (Alternative Encoding)

Nominal attributes có thể chuyển đổi sang dạng binary attribute để tính khoảng cách:

Với mỗi trạng thái (value) của thuộc tính danh nghĩa, tạo một biến nhị phân.
Nếu đối tượng mang giá trị đó → đặt 1; ngược lại → 0.
Ví dụ:
map_color có 5 màu {red, yellow, green, pink, blue} → tạo 5 cột tương ứng.
Nếu đối tượng có màu yellow, thì vector = (0, 1, 0, 0, 0).

Sau khi mã hóa nhị phân, có thể áp dụng các công thức dissimilarity hoặc similarity đã được trình bày cho binary attributes ở phần tiếp theo (2.4.3).

Proximity Measures for Binary Attributes

1. Khái niệm cơ bản

Binary attribute chỉ có hai trạng thái:
- 1 → thuộc tính hiện diện (present)
- 0 → thuộc tính vắng mặt (absent)
  Ví dụ: thuộc tính smoker:
- 1 = bệnh nhân có hút thuốc
- 0 = bệnh nhân không hút thuốc

→ Không nên xem binary như giá trị số vì 0 và 1 không có tính liên tục.

2. Các loại binary attributes

Có hai loại chính:

Symmetric binary attributes:
Hai trạng thái 0 và 1 quan trọng như nhau.
→ Dùng cho các đặc điểm như giới tính (male/female).
Asymmetric binary attributes:
Trạng thái 1 mang nhiều ý nghĩa hơn 0 (1 = “có”, 0 = “không”).
→ Dùng cho các thuộc tính như có bệnh, có triệu chứng, kết quả dương tính,…

3. Bảng 2×2 Contingency Table

Object i	Object j = 1	Object j = 0	Tổng
1	q	r	q + r
0	s	t	s + t
Tổng	q + s	r + t	p (= q + r + s + t)

Giải thích:

$q$ : số thuộc tính mà cả hai đều = 1
$r$ : thuộc tính = 1 ở $i$ , nhưng = 0 ở $j$
$s$ : thuộc tính = 0 ở $i$ , nhưng = 1 ở $j$
$t$ : thuộc tính mà cả hai đều = 0
$p$ : tổng số thuộc tính

4. Symmetric Binary Dissimilarity

Với symmetric attributes (0 và 1 có giá trị tương đương):

$d (i, j) = \frac{r + s}{q + r + s + t}$

Dissimilarity tăng khi số lượng thuộc tính khác nhau (r + s) tăng.

5. Asymmetric Binary Dissimilarity

Với asymmetric attributes (0 không quan trọng, chỉ quan tâm đến 1):

$d (i, j) = \frac{r + s}{q + r + s}$

→ Bỏ qua các cặp (0,0) vì không mang thông tin.
Đây là Jaccard distance.

6. Asymmetric Binary Similarity

Từ đó, độ tương tự (similarity) được định nghĩa là:

$s im (i, j) = 1 - d (i, j) = \frac{q}{q + r + s}$

→ Gọi là Jaccard coefficient, rất phổ biến trong khai phá dữ liệu.

Ví dụ: → Jack và Mary có độ khác biệt thấp nhất → tương tự nhất (có thể mắc bệnh giống nhau).
Jim và Mary khác biệt nhất → ít khả năng có cùng bệnh.

Dissimilarity of Numeric Data: Minkowski Distance

2. Chuẩn hóa dữ liệu trước khi tính khoảng cách

Trước khi tính toán, dữ liệu số thường được chuẩn hóa để tránh sự chênh lệch về đơn vị đo hoặc thang giá trị.
Ví dụ: chiều cao có thể đo bằng cm hoặc inch, nếu không chuẩn hóa thì thuộc tính này sẽ ảnh hưởng quá lớn đến kết quả.

Các cách chuẩn hóa phổ biến:

Thu nhỏ dữ liệu về khoảng $[- 1, 1]$ hoặc $[0, 1]$ .
Nhằm đảm bảo mỗi thuộc tính có trọng số tương đương khi tính khoảng cách.

3. Euclidean Distance (L₂ norm)

$d (i, j) = (x_{i 1} - x_{j 1})^{2} + (x_{i 2} - x_{j 2})^{2} + \dots + (x_{i p} - x_{j p})^{2}$

Là khoảng cách “đường chim bay” giữa hai điểm trong không gian p-chiều.
Dùng phổ biến nhất khi các thuộc tính độc lập và cùng thang đo.

4. Manhattan Distance (L₁ norm)

$d (i, j) = ∣ x_{i 1} - x_{j 1} ∣ + ∣ x_{i 2} - x_{j 2} ∣ + \dots + ∣ x_{i p} - x_{j p} ∣$

Còn gọi là city block distance, giống như đi theo lưới đường phố.
Dùng tốt khi chỉ muốn tính tổng chênh lệch tuyệt đối, không quan tâm hướng.

5. Các tính chất của một “metric”

Cả hai khoảng cách Euclidean và Manhattan đều thỏa mãn:

Không âm: $d (i, j) \geq 0$
Phản xạ: $d (i, i) = 0$
Đối xứng: $d (i, j) = d (j, i)$
Bất đẳng thức tam giác: $d (i, j) \leq d (i, k) + d (k, j)$

6. Minkowski Distance (Lₚ norm) – Tổng quát hóa

$d (i, j) = (\sum_{f = 1}^{p} ∣ x_{i f} - x_{j f} ∣^{h})^{1/ h}$

với $h \geq 1$ .

$h = 1 \Rightarrow$ Manhattan distance
$h = 2 \Rightarrow$ Euclidean distance
$h \to \infty \Rightarrow$ Supremum distance (Chebyshev)

7. Supremum (Chebyshev) Distance

undefined

An Hoai Thai's Notes

Trong bài này

Measuring Data Similarity and Dissimilarity