Chúng ta thường sử dụng mô hình hồi quy vào những bài toán như dự đoán một giá trị số:

Dự đoán giá cả (như giá nhà, cổ phiếu, v.v.),
Dự đoán thời gian lưu trú (ví dụ: thời gian bệnh nhân nằm viện),
Dự báo nhu cầu (chẳng hạn như doanh số bán lẻ),

Tuy nhiên, không phải mọi bài toán dự đoán đều là bài toán hồi quy cổ điển. Chúng ta sẽ tìm hiểu về các bài toán phân loại (classification), nơi mà mục tiêu là dự đoán một nhãn thuộc vào tập hợp các danh mục (categories).

Ví dụ minh họa: Giả sử chúng ta muốn ước lượng giá của các căn nhà (tính bằng đô la) dựa trên diện tích (tính bằng feet vuông) và tuổi của ngôi nhà (tính bằng năm). Để xây dựng mô hình dự đoán giá nhà, trước tiên chúng ta cần có dữ liệu thực tế, bao gồm giá bán, diện tích, và tuổi nhà cho mỗi căn. Trong ngữ cảnh của học máy:

Tập dữ liệu đó được gọi là tập huấn luyện (training dataset hoặc training set).
Mỗi dòng dữ liệu (ứng với một giao dịch bán nhà) gọi là một mẫu (example) hay còn gọi là instance / data point / sample.
Giá bán là giá trị mà chúng ta cần dự đoán, gọi là nhãn (label) hoặc mục tiêu (target).
Các biến được dùng để dự đoán (tuổi và diện tích) gọi là đặc trưng (features) hoặc biến đồng biến (covariates). Lưu ý ở đây dùng Jupyter Notebook:

%matplotlib inline  # Dùng để hiển thị biểu đồ ngay trong notebook
import math
import time
import numpy as np
import torch
from d2l import torch as d2l  # Thư viện Dive into Deep Learning sử dụng PyTorch

1. Basic

Hồi quy tuyến tính (Linear Regression) là công cụ đơn giản nhất và cũng phổ biến nhất trong số các phương pháp tiêu chuẩn dùng để giải bài toán hồi quy.

Phương pháp này đã xuất hiện từ đầu thế kỷ 19 — do Legendre (1805) và Gauss (1809) phát triển.

Giả định hồi quy tuyến tính

Giả định thứ nhất:

Mối quan hệ giữa đặc trưng (feature) và mục tiêu (target) gần như tuyến tính.

Nói cách khác, giá trị trung bình kỳ vọng của biến cần dự đoán có thể được viết dưới dạng tổng có trọng số của các đặc trưng đầu vào.
Giả định thứ hai:

Mặc dù dự đoán là tuyến tính, giá trị thực tế có thể lệch đi một chút so với dự đoán, do có yếu tố nhiễu (noise) trong quan sát.

Ta giả sử rằng nhiễu này tuân theo phân phối chuẩn (Gaussian distribution), tức là không có gì bất thường hoặc cực đoan.

Một số ký hiệu thường dùng trong mô hình:

$n$ : số lượng mẫu (ví dụ) trong tập dữ liệu
$x^{(i)}$ : mẫu thứ $i$ (số trên là superscript để đánh số mẫu)
$x_{j}^{(i)}$ : đặc trưng (tọa độ) thứ $j$ của mẫu thứ $i$

Nói dễ hiểu: nếu bạn có 100 ngôi nhà và mỗi ngôi nhà có 2 đặc trưng (diện tích và tuổi), thì:

$x^{(17)}$ : là thông tin của ngôi nhà thứ 17

$x_{1}^{(17)}$ : là diện tích của ngôi nhà thứ 17

$x_{2}^{(17)}$ : là tuổi của ngôi nhà đó

1.1. Model

Trái tim của mọi mô hình học máy là một hàm số mô tả cách các đặc trưng (feature) được chuyển đổi thành dự đoán (ước lượng) của nhãn (label).

Từ giả định tuyến tính (giả định thứ nhất) ta có: Giá trị kỳ vọng của nhãn (ví dụ: giá nhà) có thể được viết dưới dạng tổng có trọng số của các đặc trưng (diện tích, tuổi nhà).

Biểu thức toán học tuyến tính đơn giản: Ví dụ mô hình: $\overset{y}{^} = w_{1} \cdot x_{1} + w_{2} \cdot x_{2} + b$ Trong đó:

$\overset{y}{^}$ : giá nhà dự đoán
$x_{1}$ : diện tích
$x_{2}$ : tuổi nhà
$w_{1}, w_{2}$ : trọng số (weights), nói lên mức độ ảnh hưởng của mỗi đặc trưng
$b$ : hằng số dịch chuyển (bias), còn gọi là hệ số chặn (intercept)

Có thể gọi

$y$ : response/target/dependent variable

$x$ : Predictor/feature/independent/input variable

$w$ : Regression coefficient/weight/parameter

Dù không có ngôi nhà nào thật sự có diện tích = 0 và tuổi = 0, ta vẫn cần có $b$ để mô hình có thể linh hoạt, không bị giới hạn phải đi qua gốc tọa độ (0,0).

→ Về mặt hình học, đây là phép biến đổi affine, tức là tuyến tính cộng với dịch chuyển.

Biểu diễn ngắn gọn bằng đại số tuyến tính (cho dữ liệu nhiều chiều)

Khi số lượng đặc trưng nhiều (gọi là ddd), ta cần cách viết ngắn gọn hơn. Thay vì viết từng biến, ta gom:

Tập hợp đặc trưng: $x = [x_{1}, x_{2}, ..., x_{d}]^{⊤}$
Tập trọng số: $w = [w_{1}, w_{2}, ..., w_{d}]^{⊤}$
Kí hiệu T là là phép chuyển vị (transpose) trong đại số tuyến tính:
- Nếu $A \in R^{m \times n}$ thì $A^{T} \in R^{n \times m}$ và $(A^{T})_{ij} = A_{ji}$
- Với vector, $[x_{1}, x_{2}, \dots, x_{d}]^{T}$ , nghĩa là vector cột kích thước $d \times 1$ . Còn $[x_{1}, \dots, x_{d}]$ (không T) thường hiểu là vector hàng $1 \times d$ .
- $A A^{T} x = [142536] \in R^{2 \times 3}, = 123456 \in R^{3 \times 2} . = 123, x^{T} = [123] .$ Ta viết lại mô hình: $\overset{y}{^} = w^{⊤} x + b$

Đây là tích vô hướng (dot product) giữa vector trọng số và vector đặc trưng, cộng thêm bias. $\overset{y}{^} = [w_{1} w_{2} \dots w_{d}] x_{1} x_{2} ⋮ x_{d} + b = \sum_{j = 1}^{d} w_{j} x_{j} + b$ Nếu viết cho toàn bộ n mẫu: $\hat{y} = Xw + b$

trong đó $X \in R^{n \times d}$ , mỗi hàng là $x^{(i) ⊤}$ . Mục tiêu của hồi quy tuyến tính là tìm vector trọng số 𝑤 và hệ số chặn 𝑏 sao cho, khi cho trước đặc trưng của một mẫu dữ liệu mới được lấy từ cùng phân phối với 𝑋 , nhãn của mẫu mới này sẽ (theo kỳ vọng) được dự đoán với sai số nhỏ nhất.

Nhiễu

Ngay cả khi chúng ta tin rằng mô hình tốt nhất để dự đoán $y$ từ $x$ là tuyến tính, ta cũng không kỳ vọng tìm thấy một tập dữ liệu thực tế gồm $n$ mẫu mà $y^{(i)}$ bằng chính xác $w^{⊤} x^{(i)} + b$ với mọi $1 \leq i \leq n$ . Ví dụ: Bất kể công cụ nào chúng ta dùng để đo các đặc trưng $x$ và nhãn $y$ , vẫn có thể tồn tại một lượng nhỏ nhiễu đo lường. Do đó, ngay cả khi chúng ta tin tưởng rằng mối quan hệ cơ bản là tuyến tính, ta vẫn cần đưa vào thành phần nhiễu để tính đến những sai số này. Vì vậy Trước khi có thể bắt đầu tìm các tham số tốt nhất (hay tham số mô hình) $w$ và $b$ , chúng ta sẽ cần thêm hai yếu tố:

Một thước đo để đánh giá chất lượng của một mô hình cho trước
Một quy trình để cập nhật mô hình nhằm cải thiện chất lượng của nó.

1.2. Loss Function

Việc khớp mô hình với dữ liệu đương nhiên đòi hỏi chúng ta phải thống nhất về một thước đo mức độ phù hợp (hay tương đương, mức độ không phù hợp). Hàm mất mát (loss function) định lượng khoảng cách giữa giá trị thật và giá trị dự đoán của biến mục tiêu. Giá trị mất mát thường là một số không âm, trong đó giá trị nhỏ hơn biểu thị mô hình tốt hơn, và dự đoán hoàn hảo sẽ có mất mát bằng 0.

Sum of Squared Errors (SSE)

Đối với bài toán hồi quy, hàm mất mát phổ biến nhất là bình phương sai số (squared error). Khi dự đoán cho một mẫu $x^{(i)}$ là $\overset{y}{^}^{(i)}$ và nhãn thật tương ứng là $y^{(i)}$ $ℓ^{(i)} (w, b) = \frac{1}{2} (\overset{y}{^}^{(i)} - y^{(i)})^{2}$ Hằng số $\frac{1}{2}$ không ảnh hưởng đến bản chất của mất mát, nhưng tiện lợi về ký hiệu vì nó triệt tiêu khi lấy đạo hàm. $\frac{d}{d y ^} \frac{1}{2} (\overset{y}{^} - y)^{2} = (\overset{y}{^} - y)$ Vì tập huấn luyện đã được cho sẵn (ngoài tầm kiểm soát của ta), nên sai số kinh nghiệm (empirical error) chỉ là hàm của tham số mô hình. Trong hình dưới, ta minh họa việc khớp một mô hình hồi quy tuyến tính cho dữ liệu đầu vào 1 chiều. image 43.png

Lưu ý: Sai khác lớn giữa $\overset{y}{^}^{(i)}$ và $y^{(i)}$ tạo ra đóng góp lớn hơn nhiều cho mất mát do dạng bình phương của nó. Điều này có thể là con dao hai lưỡi: vừa giúp mô hình tránh lỗi lớn, vừa có thể khiến mô hình quá nhạy cảm với điểm bất thường. Để đo chất lượng mô hình trên toàn bộ tập dữ liệu gồm $n$ mẫu, ta lấy trung bình (hoặc tương đương, tổng) mất mát trên tập huấn luyện: Mean Squared Error (MSE) $L (w, b) = \frac{1}{n} \sum_{i = 1}^{n} ℓ^{(i)} (w, b)$ Tính chất quan trọng của MSE

Ưu điểm: phạt mạnh lỗi lớn → mô hình hạn chế sai số nghiêm trọng.
Nhược điểm: nhạy với outlier → đôi khi cần hàm mất mát thay thế như MAE hoặc Huber Loss. Khi huấn luyện mô hình, ta tìm bộ tham số $(w, b)$ sao cho tối thiểu hóa tổng mất mát trên tất cả mẫu huấn luyện: $(w^{*}, b^{*}) = ar g min_{w, b} L (w, b)$
Câu hỏi đào sâu:
- Tại sao hàm mất mát không được có giá trị âm?
  
  → “Sai” thì không thể mang giá trị âm, vì âm sẽ không còn phản ánh trực quan “mức độ tệ” nữa.

1.3. Nghiệm giải tích (Analytic Solution)

So với các mô hình khác thì hồi quy tuyến tính mang đến một bài toán tối ưu đáng ngạc nhiên là dễ giải. Cụ thể, ta có thể tìm tham số tối ưu (đánh giá trên tập huấn luyện) một cách giải tích bằng công thức đơn giản sau: Bước “hấp thụ bias”: Thêm cột 1 vào $X$ → $b$ trởi thành phần tử đầu tiên của $w$ → công thức gọn hơn: $\hat{y} = \overset{ˉ}{X} \overset{ˉ}{w}$ Với $\overset{ˉ}{X} \in R^{n \times (d + 1)}$ Khi đó, bài toán dự đoán trở thành tối thiểu hóa hàm mất mát MSE.

Miễn là ma trận thiết kế $X$ có hạng đầy đủ (full rank, tức là không có đặc trưng nào phụ thuộc tuyến tính vào đặc trưng khác), thì sẽ chỉ có một điểm tới hạn trên bề mặt hàm mất mát, và điểm này tương ứng với nghiệm tối thiểu toàn cục. Lấy đạo hàm: $\nabla_{w} L (w) = 0 \Rightarrow X^{⊤} X w = X^{⊤} y$ Giải ra $w$ ta thu được nghiệm tối ưu của bài toán: $w^{*} = (X^{⊤} X)^{- 1} X^{⊤} y$ Điều kiện khả nghịch: Nghiệm này chỉ duy nhất khi ma trận $X^{⊤} X$ khả nghịch (invertible), tức các cột của $X$ độc lập tuyến tính. Nếu không khả nghịch (đa cộng tuyến), ta cần kỹ thuật như giải pháp Moore–Penrose pseudoinverse hoặc regularization (Ridge). Ưu điểm:

Nhanh và chính xác về mặt toán học với dữ liệu nhỏ–vừa.
Không cần lặp lại nhiều lần. Nhược điểm:
Tính toán $(X^{⊤} X)^{- 1}$ tốn kém với dữ liệu lớn.
Không áp dụng được với các mô hình phi tuyến hoặc phức tạp (như deep learning). Mặc dù các bài toán đơn giản như hồi quy tuyến tính có thể có nghiệm giải tích, nhưng đừng quá trông chờ vào may mắn này. Yêu cầu về nghiệm giải tích rất hạn chế và sẽ loại bỏ gần như toàn bộ các khía cạnh thú vị của học sâu (deep learning).

1.4. Gradient Descent Ngẫu nhiên Theo Minibatch (Minibatch Stochastic Gradient Descent – SGD)

Gradient Descent

Huấn luyện mô hình học sâu thường không thể tìm được nghiệm giải tích như hồi quy tuyến tính. Tuy vậy, trong thực tế, ta vẫn có thể huấn luyện hiệu quả bằng các phương pháp tối ưu lặp (iterative optimization), trong đó phổ biến nhất là Gradient Descent – cập nhật tham số theo hướng giảm giá trị hàm mất mát. Gradient Descent cơ bản tính gradient dựa trên toàn bộ dữ liệu huấn luyện trước mỗi lần cập nhật. Cách này chính xác nhưng rất chậm khi dữ liệu lớn và có thể lãng phí do dữ liệu trùng lặp thông tin. 💡 Tip: Trong học sâu, tốc độ huấn luyện quan trọng không kém độ chính xác gradient. Không nhất thiết phải dùng toàn bộ dữ liệu cho mỗi lần cập nhật.

Câu hỏi gợi mở:
- Vì sao gradient descent toàn bộ dữ liệu (full batch) có thể chậm?
  - Chi phí tính toán cao: Mỗi bước cần đọc và xử lý toàn bộ dữ liệu ⇒ với dataset lớn (hàng triệu mẫu), một bước update có thể mất nhiều giây/phút, dẫn đến tốc độ hội tụ rất chậm.
  - Không tận dụng cập nhật sớm: Dù gradient đã đủ “ổn định” từ vài nghìn mẫu, ta vẫn phải tính thêm trên toàn bộ dataset trước khi cập nhật tham số.
- Tình huống nào dữ liệu huấn luyện có tính dư thừa cao?
  - Dữ liệu được nhân bản (data duplication), ví dụ khi crawl web, nhiều bản copy cùng một ảnh hoặc văn bản.
  - Lặp mẫu với nhiễu nhỏ (same sample + noise), ví dụ ảnh cùng góc chụp nhưng độ sáng khác nhau rất ít.
  - Mẫu gần tuyến tính phụ thuộc: Các vector đặc trưng gần như nằm trên cùng một mặt phẳng con ⇒ gradient đóng góp rất giống nhau.
  - Mẫu từ cùng phân phối con (sub-distribution bias), ví dụ 90% ảnh đều thuộc một vài lớp dễ phân biệt, còn các lớp khó chỉ chiếm tỷ lệ nhỏ.
- Ngoài tốc độ, full batch còn hạn chế gì khi huấn luyện mô hình lớn?
  - Không có nhiễu để giúp thoát local min
  - Yêu cầu bộ nhớ lớn
  - Khó parallel hóa hiệu quả
  - Không phản hồi sớm
  - Hội tụ kém khi dữ liệu không đồng nhất

Stochastic Gradient Descent (SGD)

Chỉ dùng một mẫu cho mỗi lần cập nhật. Cách này nhanh hơn nhưng lại gặp hai vấn đề:

Hiệu suất phần cứng kém: Về mặt tính toán, bộ xử lý tính nhân–cộng số nhanh hơn nhiều so với việc chuyển dữ liệu từ bộ nhớ chính vào bộ nhớ đệm CPU. Thực hiện một phép nhân ma trận–vector có thể hiệu quả hơn đến cả bậc độ lớn so với số lượng tương ứng các phép nhân vector–vector. Điều này nghĩa là xử lý từng mẫu một có thể mất nhiều thời gian hơn so với xử lý nguyên một batch.
Một số lớp đặc biệt (vd: batch normalization) yêu cầu nhiều hơn một mẫu để hoạt động tốt.

Chiến lược Minibatch SGD

Minibatch SGD là giải pháp dung hòa:

Không dùng toàn bộ dữ liệu như full batch.
Không dùng 1 mẫu như SGD thuần.
Thay vào đó, lấy một nhóm nhỏ (minibatch) kích thước (thường từ 32–256, bội số của 2) để tính gradient. Kích thước minibatch phụ thuộc vào:
Dung lượng bộ nhớ.
Số lượng GPU/TPU.
Kiến trúc mô hình.
Kích thước tập dữ liệu. 💡 Tip: Minibatch vừa giúp tận dụng phần cứng, vừa giảm nhiễu so với SGD thuần, đồng thời cập nhật nhanh hơn full batch.
Câu hỏi gợi mở
1. Vì sao batch size thường chọn là bội số của 2?
2. Batch size lớn quá sẽ gây tác động gì đến quá trình hội tụ?
3. Trong trường hợp bộ nhớ hạn chế, nên ưu tiên batch size bao nhiêu?

Quy trình cập nhật

Với mỗi vòng lặp $t$ :

Lấy minibatch $B_{t}$ gồm $m$ mẫu ngẫu nhiên
Tính gradient trung bình trên minibatch:

$g_{t} = \frac{1}{m} \sum_{i \in B_{t}} \nabla_{θ} ℓ^{(i)} (θ)$
Cập nhật tham số:

$θ \leftarrow θ - η \cdot g_{t}$

Với $η$ là learning rate

Câu hỏi gợi mở
- Vì sao learning rate và batch size được coi là hyperparameter?
  - Tham số (parameters): Là những giá trị mô hình tự học được qua quá trình tối ưu (ví dụ: trọng số w và bias b trong mạng neural).
  - Siêu tham số (hyperparameters): Là những giá trị bạn phải đặt trước khi bắt đầu huấn luyện, chúng không được cập nhật qua gradient descent.

Tính chất và thực tế áp dụng

Hyperparameters: batch size, learning rate do người dùng chọn, có thể tinh chỉnh bằng kỹ thuật như Bayesian Optimization.
Tính không tất định: kết quả huấn luyện khác nhau mỗi lần chạy do chọn minibatch ngẫu nhiên.
Mục tiêu: không cần tìm chính xác nghiệm tối ưu toàn cục, chỉ cần bộ tham số dự đoán tốt trên dữ liệu mới (tổng quát hóa).
Trong deep learning: dễ tìm nghiệm tốt trên tập huấn luyện; khó hơn là đạt hiệu suất tốt trên tập chưa thấy. 💡 Tip: Đánh giá mô hình nên dùng tập validation độc lập để đo khả năng tổng quát hóa.

1.5. Dự đoán (Predictions)

Khi đã huấn luyện xong mô hình $(w, b)$ , ta có thể dự đoán giá trị đầu ra cho mẫu mới. Ví dụ: dự đoán giá bán của một căn nhà chưa từng thấy trước đó dựa trên diện tích $x_{1}$ và tuổi nhà $x_{2}$ . Công thức dự đoán: $\overset{y}{^} = w^{⊤} x + b$

Trong cộng đồng deep learning, giai đoạn dự đoán thường được gọi là inference. Tuy nhiên:

Trong nghĩa rộng, inference là bất kỳ kết luận nào rút ra từ dữ liệu, bao gồm:
- Suy luận về tham số mô hình (parameter inference).
- Dự đoán nhãn cho mẫu mới.
Trong thống kê, inference thường chỉ ước lượng tham số hơn là dự đoán đầu ra. Việc dùng chung thuật ngữ “inference” cho dự đoán trong deep learning đôi khi gây nhầm lẫn khi trao đổi với nhà thống kê. Note!: Để tránh mơ hồ, trong tài liệu này ưu tiên dùng từ “prediction” khi nói về dự đoán giá trị/nhãn cho dữ liệu mới.

2. Vector hóa để tăng tốc (Vectorization for Speed)

Khi huấn luyện mô hình, ta thường muốn xử lý toàn bộ minibatch cùng lúc thay vì từng mẫu riêng lẻ. Để làm điều này hiệu quả, cần vector hóa các phép tính và tận dụng thư viện đại số tuyến tính tối ưu (BLAS, cuBLAS…) thay vì viết vòng lặp for tốn kém trong Python. Vector hóa giúp tận dụng tối đa khả năng tính toán song song của CPU/GPU và giảm overhead của Python. Giả sử ta có hai vector $a, b$ 10,000 chiều, tất cả phần tử = 1.

import torch, time
n = 10000
a = torch.ones(n)
b = torch.ones(n)

Cách 1: Duyệt từng phần tử bằng for loop.

# Cách 1: for-loop
c = torch.zeros(n)
t = time.time()
for i in range(n):
    c[i] = a[i] + b[i]
print(f'{time.time() - t:.5f} sec')  # ~0.17802 sec

Cách 2: Cộng toàn bộ vector bằng phép toán + của thư viện.

# Cách 2: vector hóa
t = time.time()
d = a + b
print(f'{time.time() - t:.5f} sec')  # ~0.00036 sec

Kết quả: Cách 2 nhanh hơn hàng trăm lần so với cách 1. Điều này là bởi vì khi cộng vector, phép toán a + b trong PyTorch/NumPy gọi tới hàm C/C++ tối ưu, chạy nhanh hơn nhiều so với vòng lặp Python. Hơn thế nữa:

Tốc độ: thường tăng theo bậc độ lớn (order-of-magnitude speedup).
Ít lỗi: giảm số lượng phép tính thủ công.
Tính di động: code dễ chuyển sang chạy trên GPU hoặc phần cứng khác.
Câu hỏi gợi mở:
- Làm sao để phát hiện đoạn code có thể vector hóa?
  - Dấu hiệu 1 – Vòng lặp phần tử độc lập: mẫu dạng
    
    for i in range(n): y[i] = f(x[i]) → thường thay bằng ufunc: y = f(x).
  - Dấu hiệu 2 – Map–Reduce: vòng lặp tính rồi cộng dồn (+=) → dùng reductions (sum/mean/logsumexp).
  - Dấu hiệu 3 – Toán có thể viết bằng broadcasting: thay nested loops kết hợp chỉ số bằng einsum/matmul/broadcast.
  - Dấu hiệu 4 – Điều kiện theo phần tử: if/else per-element → where hoặc mask: y = np.where(cond, a, b).
  - Dấu hiệu 5 – Sliding window/convolution: tự cuộn vòng lặp cửa sổ → dùng conv1d/2d hoặc as_strided (cẩn thận).
  - Dấu hiệu 6 – Lặp theo trục: for j in range(d): thao tác cột/hàng → dùng ops theo axis.

3. Phân phối chuẩn và hàm mất mát bình phương (The Normal Distribution and Squared Loss)

Động cơ xác suất cho squared loss

Trước đây, ta đã lý giải squared loss ở góc nhìn chức năng:

Nếu quan hệ thực sự tuyến tính, nghiệm tối ưu trả về kỳ vọng có điều kiện $E [y ∣ x]$ .
Hàm mất mát phạt mạnh outlier. Ta có thể đưa ra động cơ hình thức hơn bằng cách giả định xác suất cho phân phối nhiễu. Vì khi liên hệ squared loss với phân phối chuẩn, ta mở rộng được phương pháp sang nhiều mô hình xác suất khác.
Câu hỏi gợi mở:
- Vì sao squared loss trả về kỳ vọng có điều kiện?
  
  Với một mô hình dự đoán $\overset{y}{^} = f_{θ} (x)$ , hàm mất mát squared loss trên phân phối thật $(x, y)$ là: $L (θ) = E_{(x, y)} [(y - f_{θ} (x))^{2}]$
  
  Nếu ta tối ưu theo hàm dự đoán $f (x)$ tại từng giá trị $x$ (coi $x$ cố định), bài toán trở thành: $min_{a} E [(y - a)^{2} x]$
  
  Ở đây $a$ là giá trị dự đoán tại điểm $x$ .
  
  Ta khai triển bình phương: $E [(y - a)^{2} x] = E [y^{2} ∣ x] - 2 a E [y ∣ x] + a^{2}$
  
  Lấy đạo hàm theo $a$ : $\frac{\partial}{\partial a} = - 2 E [y ∣ x] + 2 a$
  
  Cho bằng 0 để tìm cực tiểu: $- 2 E [y ∣ x] + 2 a = 0 \Rightarrow a = E [y ∣ x]$
  
  Từ đó ta được điều phải chứng minh. Giá trị $a$ (hay dự đoán tối ưu $f^{*} (x)$ ) chính là kỳ vọng có điều kiện của $y$ khi biết $x$ : $f^{*} (x) = E [y ∣ x]$
- Outlier ảnh hưởng thế nào đến squared loss?
  
  Bình phương phóng đại sai số lớn
  - Sai số $(y - \overset{y}{^})$ được bình phương, nên nếu một điểm lệch nhiều khỏi dự đoán (outlier), giá trị bình phương sẽ tăng theo cấp số nhân.
  Kéo dịch nghiệm về phía outlier
  - Vì squared loss tối ưu mean có điều kiện, nên một vài giá trị quá lớn hoặc quá nhỏ sẽ “kéo” trung bình, khiến mô hình dịch dự đoán để giảm ảnh hưởng sai số đó, dù làm giảm độ chính xác với phần lớn điểm dữ liệu khác.
  Hệ quả
  - Mô hình có thể dự đoán lệch đáng kể cho các điểm “bình thường” chỉ để giảm lỗi lớn ở vài điểm outlier.
  - Tính ổn định giảm, đặc biệt khi dữ liệu nhiễu mạnh.
- Có thể chọn hàm mất mát nào khác khi dữ liệu có phân phối nhiễu khác chuẩn?
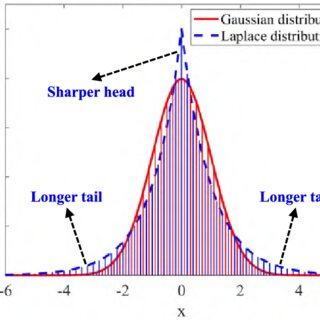
  Nhiễu phân phối Laplace (đuôi dày hơn Gaussian)
  Sao Laplace đuôi dày hơn Gaussian:
  
  Gaussian (chuẩn)
  
  PDF: $p (x) = \frac{1}{2 π σ ^{2}} e^{- \frac{x ^{2}}{2 σ ^{2}}}$
  
  Khi $∣ x ∣ \to \infty$ , xác suất giảm theo hàm mũ của bình phương ( $e^{- x^{2}}$ ) → giảm rất nhanh → đuôi mỏng.
  
  Laplace:
  
  PDF: $p (x) = \frac{1}{2 b} e^{- \frac{∣ x ∣}{b}}$
  
  Khi $∣ x ∣ \to \infty$ , xác suất giảm theo hàm mũ tuyến tính ( $e^{- ∣ x ∣}$ ) → giảm chậm hơn → đuôi dày hơn
  - Phân phối giả định: $p (ϵ) = \frac{1}{2 b} exp (- \frac{∣ ϵ ∣}{b})$
  - Hàm mất mát tương đương: MAE (Mean Absolute Error)
    
    $L (w) = \frac{1}{n} \sum_{i = 1}^{n} ∣ y_{i} - \overset{y}{^}_{i} ∣$
  - Ưu điểm: Ít nhạy cảm với outlier hơn MSE.
  Nhiễu phân phối Poisson (dữ liệu đếm, không âm)
  - Phân phối giả định: $p (y ∣ λ) = \frac{λ ^{y} e ^{- λ}}{y !}$
  - Hàm mất mát: Negative log-likelihood (NLL) Poisson
    
    $L = \frac{1}{n} \sum_{i = 1}^{n} (\overset{y}{^}_{i} - y_{i} lo g \overset{y}{^}_{i})$
  - Ứng dụng: Số lượt truy cập web, số ca bệnh, số sản phẩm bán ra.

Nhiễu phân phối Bernoulli (dữ liệu nhị phân)

Phân phối giả định: $p (y ∣ p) = p^{y} (1 - p)^{1 - y}$

Hàm mất mát: Binary Cross-Entropy

$L = - \frac{1}{n} \sum_{i = 1}^{n} (y_{i} lo g \overset{p}{^}_{i} + (1 - y_{i}) lo g (1 - \overset{p}{^}_{i}))$

Ứng dụng: Phân loại 0/1.

    > [!important] **Nhiễu phân phối Heavy-tailed (đuôi rất dày, nhiều outlier)**
    > 
    > - **Hàm mất mát: Huber loss**
    > 
    > $$L_\delta(e) =\begin{cases}  \frac{1}{2} e^2 & \text{nếu } |e| \le \delta \\  \delta(|e| - \frac{1}{2}\delta) & \text{nếu } |e| > \delta\end{cases}$$
    > 
    > - **Ưu điểm:** Kết hợp ưu điểm của MSE (ổn định khi lỗi nhỏ) và MAE (chịu outlier tốt).
    
- Làm sao để biết nhiễu sẽ tuân theo phân phối nào
    
    a) **Vẽ histogram & so sánh trực quan**
    
    - Lấy phần dư (residuals):
        
        $ei=yi−y^ie_i = y_i - \hat{y}_iei=yi−y^i$
        
    - Vẽ histogram, so với đường cong PDF Gaussian, Laplace, Poisson...
    - Nếu đuôi dài hơn nhiều so với Gaussian → có thể là Laplace hoặc heavy-tailed.
    
    ---
    
    b) **Q-Q plot (Quantile-Quantile plot)**
    
    - Vẽ các quantile thực tế của residuals so với quantile lý thuyết của phân phối giả định.
    - Nếu là đường thẳng → dữ liệu phù hợp với phân phối đó.
    - Nếu đuôi cong ra xa → có heavy-tail.
    
    ---
    
    c) **Thống kê mô tả**
    
    - So sánh **kurtosis** (độ nhọn):
        - Gaussian có kurtosis = 3
        - Laplace ≈ 6 (đuôi dày hơn)
        - Heavy-tailed > 6
    - So sánh **skewness** (độ lệch) để xem dữ liệu có đối xứng không.
    
    ---
    
    d) **Kiểm định giả thuyết thống kê**
    
    - **Shapiro–Wilk test** / **Kolmogorov–Smirnov test** cho Gaussian.
    - **Anderson–Darling test** để kiểm định phân phối bất kỳ.
    - Chạy MLE fit với nhiều phân phối, so sánh **AIC / BIC** để chọn mô hình tốt nhất.
- ==Nếu dùng== ==**SAE**== ==(Sum of Absolute Errors) thay cho== ==**SSE**== ==(Sum of Squared Errors) được không?==
    
    - $\text{SAE} = \sum_{i=1}^n \left| y_i - \hat{y}_i \right|$
    
    |Tiêu chí|SSE|SAE|
    |---|---|---|
    |**Độ nhạy với outlier**|Rất nhạy (outlier bị phóng đại do bình phương)|Ít nhạy hơn, vì lỗi chỉ tăng tuyến tính|
    |**Giải tích (analytic solution)**|Có thể giải dễ dàng bằng đạo hàm (ví dụ hồi quy tuyến tính có công thức đóng)|Không khả vi tại $e_i = 0$ → không có công thức đóng, phải dùng tối ưu số|
    |**Ý nghĩa thống kê**|Tương ứng với giả định nhiễu tuân theo phân phối **Gaussian**|Tương ứng với giả định nhiễu tuân theo phân phối **Laplace** (đuôi dày hơn Gaussian)|
    |**Độ trơn (smoothness)**|Hàm mục tiêu trơn, gradient rõ ràng|Hàm mục tiêu góc tại 0, gradient không xác định tại điểm lỗi = 0|
    |**Tốc độ tối ưu**|Thường nhanh hơn với gradient descent|Chậm hơn vì cần giải bài toán quy hoạch tuyến tính hoặc dùng phương pháp subgradient|
    
    > [!important] **Nhắc lại về không khả vi:**
    > 
    > Đạo hàm tại $x_0$ chỉ tồn tại khi **giới hạn đạo hàm một phía trái** và **một phía phải** đều tồn tại **và bằng nhau**:
    > 
    > $$f'(x_0) = \lim_{h \to 0^+} \frac{f(x_0+h) - f(x_0)}{h}= \lim_{h \to 0^-} \frac{f(x_0+h) - f(x_0)}{h}$$
    > 
    > Nếu một trong hai giới hạn không tồn tại, hoặc tồn tại nhưng khác nhau → hàm **không khả vi** tại điểm đó.
    > 
    > **Các nguyên nhân khiến hàm không khả vi**
    > 
    > 1. **Góc nhọn (corner / cusp)**
    >     
    >     Ví dụ: $f(x) = |x|$ tại $x = 0$
    >     
    >     Lưu ý: Hàm này vẫn liên tục
    >     
    >     - Trái: $f'(0^-) = -1$
    >     - Phải $f'(0^+) = 1$
    >     
    >     → Không bằng nhau ⇒ Không khả vi tại $x=0$.
    >     
    > 2. **Bước nhảy (discontinuity)**
    >     
    >     Ví dụ: $f(x) = \begin{cases} 1, & x \ge 0 \\ 0, & x < 0 \end{cases}$
    >     
    >     → Không liên tục ⇒ cũng không khả vi.
    >     
    > 3. Đạo hàm vô hạn (vertical tangent)
    >     
    >     Ví dụ: $f(x) = \sqrt[3]{x}$ tại $x = 0$ có đạo hàm tiến tới vô cực ⇒ không khả vi.
    >     
    
    Nếu giả định:
    
    - **Nhiễu Gaussian** → **MLE** dẫn đến **SSE** (hàm mất mát bình phương).
    - **Nhiễu Laplace** → **MLE** dẫn đến **SAE** (hàm mất mát trị tuyệt đối). (Được nhắn đến ở trên)

Phân phối chuẩn

Phân phối chuẩn (Gaussian) với trung bình $μ$ và phương sai $σ^{2}$ có hàm mật độ: $p (x) = \frac{1}{2 π σ ^{2}} exp (- \frac{( x - μ ) ^{2}}{2 σ ^{2}})$ Đặc điểm:

Thay đổi $μ$ → tịnh tiến đồ thị theo trục $x$ .
Tăng $σ^{2}$ → phân phối trải rộng ra, đỉnh thấp hơn. Code minh họa:

import math, numpy as np
import matplotlib.pyplot as plt
def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 * (x - mu)**2 / sigma**2)
x = np.arange(-7, 7, 0.01)
params = [(0, 1), (0, 2), (3, 1)]
for mu, sigma in params:
    plt.plot(x, normal(x, mu, sigma), label=f'mean {mu}, std {sigma}')
plt.xlabel('x'); plt.ylabel('p(x)'); plt.legend(); plt.show()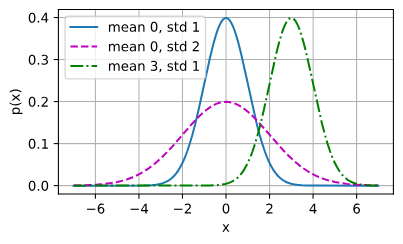

image 2 11.png Ta có thể biết là nhiều mô hình thống kê giả định nhiễu tuân theo phân phối chuẩn vì tính đối xứng và các tính chất toán học thuận lợi.

Liên hệ với hồi quy tuyến tính

Giả sử dữ liệu sinh ra từ: $y = w^{⊤} x + b + ε$ Với $ε \sim N (0, σ^{2})$ hay là e tuân theo phân phối chuẩn. Ta viết lại e theo quan sát và dự đoán: $ε = y - (w^{⊤} x + b)$ Xác suất quan sát một mẫu $(x, y)$ cho trước: $p (ε) = \frac{1}{2 π σ ^{2}} exp (- \frac{ε ^{2}}{2 σ ^{2}})$ $p (y ∣ x) = \frac{1}{2 π σ ^{2}} exp (- \frac{( y - ( w ^{⊤} x + b ) ) ^{2}}{2 σ ^{2}})$

Nguyên tắc hợp lý cực đại (MLE): chọn $w, b$ để tối đa hóa xác suất toàn bộ tập dữ liệu: $max_{w, b} \prod_{i = 1}^{n} p (y^{(i)} ∣ x^{(i)})$ Vì các mẫu độc lập, tích trên có thể lấy log để chuyển thành tổng.

Từ MLE đến squared loss

Hàm khả năng (Likelihood function): Với $n$ quan sát độc lập, xác suất đồng thời là tích của từng xác suất riêng lẻ: $L (w, b) = \prod_{i = 1}^{n} p (y_{i} ∣ x_{i}; w, b)$ $= \prod_{i = 1}^{n} \frac{1}{2 π σ ^{2}} exp (- \frac{( y _{i} - ( w ^{⊤} x _{i} + b ) ) ^{2}}{2 σ ^{2}})$ Lấy log-likelihood → hàm mục tiêu trở thành tổng của các hạng tử $- \frac{( y - y ^ ) ^{2}}{2 σ ^{2}}$ cộng hằng số. Do $l o g$ là hàm đơn điệu nên lấy log để dễ tính toán: $ℓ (w, b) = lo g L (w, b) = \sum_{i = 1}^{n} lo g [\frac{1}{2 π σ ^{2}} exp (- \frac{( y _{i} - ( w ^{⊤} x _{i} + b ) ) ^{2}}{2 σ ^{2}})]$ Tách log: $ℓ (w, b) = \sum_{i = 1}^{n} [- \frac{1}{2} lo g (2 π σ^{2}) - \frac{( y _{i} - ( w ^{⊤} x _{i} + b ) ) ^{2}}{2 σ ^{2}}]$ Đổi dấu (tối đa hóa ↔ tối thiểu hóa) → negative log-likelihood (NLL): $NLL (w, b) = - ℓ (w, b) = \frac{n}{2} lo g (2 π σ^{2}) + \frac{1}{2 σ ^{2}} \sum_{i = 1}^{n} (y_{i} - (w^{⊤} x_{i} + b))^{2}$

$\frac{n}{2} lo g (2 π σ^{2})$ không ảnh hưởng đến tối ưu hóa (không phụ thuộc vào $w, b$ ), nên bỏ qua. Còn lại: $NLL (w, b) \propto \sum_{i = 1}^{n} (y_{i} - (w^{⊤} x_{i} + b))^{2}$ Bài toán MLE với giả định nhiễu Gaussian tương đương với bài toán tối thiểu hóa tổng bình phương sai số (Squared Loss): $min_{w, b} \sum_{i = 1}^{n} (y_{i} - (w^{⊤} x_{i} + b))^{2}$ Nếu chia cho $n$ , ta được: $min_{w, b} \frac{1}{n} \sum_{i = 1}^{n} \frac{( y ^{(i)} - y ^ ^{(i)} ) ^{2}}{2 σ ^{2}}$ Nếu $σ^{2}$ cố định, bỏ hằng số $\frac{1}{2 σ ^{2}}$ → chính là MSE. Từ đó ta thấy MSE không chỉ là lựa chọn “tiện tay” mà còn xuất phát từ giả định nhiễu Gaussian và nguyên tắc MLE.

4. Linear Regression as a Neural Network

4.1. Hồi quy tuyến tính như một mạng nơ-ron một lớp

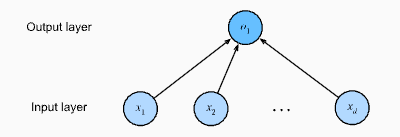
Mô hình tuyến tính có thể được xem như một mạng nơ-ron nhân tạo 1 lớp: mỗi đặc trưng là một nơ-ron đầu vào, tất cả kết nối đầy đủ đến một nơ-ron đầu ra. Cách nhìn này giúp nối hồi quy tuyến tính với các khái niệm NN như trọng số, bias, lớp tuyến tính, hàm kích hoạt. Ở lớp đầu vào có $d$ đặc trưng $x \in R^{d}$ . Lớp đầu ra gồm 1 nơ-ron cho bài toán dự đoán một đại lượng liên tục. Mô hình: $\overset{y}{^} = w^{⊤} x + b$ Về mặt cấu trúc, đây là mạng fully-connected một lớp (một nơ-ron): mọi đầu vào đều nối tới đầu ra qua trọng số $w_{j}$ , và có bias $b$ . image 3 11.png

4.2. Liên hệ sinh học (Biology)

Một nơ-ron sinh học gồm dendrite (đầu vào), nucleus (tổng hợp & xử lý), axon và axon terminals (đầu ra). Trọng số synapse điều chỉnh ảnh hưởng của tín hiệu tới nơ-ron. 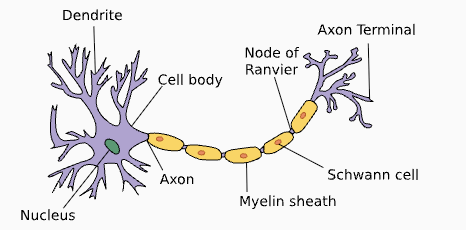image 4 8.png Tương ứng trong mô hình:

Đầu vào $x_{j}$ ↔ dendrite nhận tín hiệu.
Trọng số $w_{j}$ ↔ synaptic weight (kích thích/ức chế).
Tổng có trọng số $\sum_{j} w_{j} x_{j} + b$ ↔ tích lũy tại nucleus.
Hàm kích hoạt $ϕ (\cdot)$ ↔ xử lý phi tuyến (ở hồi quy tuyến tính, $ϕ$ là đồng nhất). Dù NN lấy cảm hứng sinh học, thiết kế hiện đại chủ yếu dựa vào toán học, thống kê, tối ưu; tương tự “máy bay lấy cảm hứng từ chim”, nhưng không sao chép cơ chế sinh học.

Tóm tắt

Hồi quy tuyến tính chọn tham số để tối thiểu hóa squared loss trên tập huấn luyện.
Squared loss có thể được biện minh bởi MLE với giả định nhiễu Gaussian cộng.
Khía cạnh tính toán: vector hóa, minibatch SGD, và đánh giá trên dữ liệu chưa thấy.
Về kiến trúc NN: hồi quy tuyến tính = mạng 1 lớp fully-connected với $ϕ$ đồng nhất. Đọc tiếp: 3.2. Object-Oriented Design for Implementation

An Hoai Thai's Notes

Trong bài này

3.1. Linear Regression

1. Basic

Giả định hồi quy tuyến tính

1.1. Model

Biểu diễn ngắn gọn bằng đại số tuyến tính (cho dữ liệu nhiều chiều)

Nhiễu

1.2. Loss Function

Sum of Squared Errors (SSE)

1.3. Nghiệm giải tích (Analytic Solution)

1.4. Gradient Descent Ngẫu nhiên Theo Minibatch (Minibatch Stochastic Gradient Descent – SGD)

Gradient Descent

Stochastic Gradient Descent (SGD)

Chiến lược Minibatch SGD

Quy trình cập nhật

Tính chất và thực tế áp dụng

1.5. Dự đoán (Predictions)

2. Vector hóa để tăng tốc (Vectorization for Speed)

3. Phân phối chuẩn và hàm mất mát bình phương (The Normal Distribution and Squared Loss)

Động cơ xác suất cho squared loss

Phân phối chuẩn

Liên hệ với hồi quy tuyến tính

Từ MLE đến squared loss

4. Linear Regression as a Neural Network

4.1. Hồi quy tuyến tính như một mạng nơ-ron một lớp

4.2. Liên hệ sinh học (Biology)

Tóm tắt

Biểu Đồ

Bảng Nội Dung

Liên Kết Ngược