1. Vectors in NumPy
Định nghĩa:
- Trong đại số tuyến tính, vector là danh sách có thứ tự các số.
- Có hai đặc điểm chính:
- Dimensionality – số lượng phần tử trong vector.
- Orientation – hướng của vector:
- Column vector: đứng dọc (nhiều hàng, 1 cột).
- Row vector: nằm ngang (1 hàng, nhiều cột).
Ký hiệu và cách biểu diễn:
- Ký hiệu : tập hợp các vector có N phần tử thực.
- Ví dụ: nghĩa là vector có 4 phần tử thực.
- Các ví dụ: \mathbf{y} = \begin{bmatrix} 0.3 \\ -7 \end{bmatrix}, \quad \mathbf{z} = [1, 4, 5, 6]$$ * $\mathbf{x}$: vector cột 4 D * $\mathbf{y}$: vector cột 2 D * $\mathbf{z}$: vector hàng 4 D
Sự khác biệt giữa toán học và Python
- Trong toán học:
- Dimensionality = số phần tử của vector.
- Trong Python (NumPy):
- Dimensionality = số chiều hình học (shape của mảng).
- Mọi vector (cột/hàng) đều là mảng 2D trong NumPy.
- Danh sách 1D (orientationless) có shape
(3,). - Vector hàng có shape
(1, 3). - Vector cột có shape
(3, 1).
Tầm quan trọng của Orientation
- Orientation có thể gây lỗi trong các phép toán (vd: dot product, matrix multiply).
- NumPy không tự động phân biệt hàng – cột nếu không khai báo rõ.
- Quy ước:
- Mặc định vector là column vector.
- Row vector được viết là (T: transpose).
Cách tạo vector trong NumPy
import numpy as np
asList = [1, 2, 3]
asArray = np.array([1, 2, 3]) # 1D array
rowVec = np.array([[1, 2, 3]]) # row vector
colVec = np.array([[1], [2], [3]]) # column vector
print(asList) # (3,)
print(asArray.shape) # (3,)
print(rowVec.shape) # (1,3)
print(colVec.shape) # (3,1)Kết quả:
asList: (3,)
asArray: (3,)
rowVec: (1,3)
colVec: (3,1)
(rows, columns)cho biết định hướng của vector.
Geometry of Vector
Hai cách hiểu về vector
- Đại số (Algebraic interpretation):
Vector là một danh sách có thứ tự các số (ordered list of numbers). - Hình học (Geometric interpretation):
Vector là một đoạn thẳng có độ dài (magnitude) và hướng (direction) xác định.- Magnitude: độ dài của vector.
- Angle: góc giữa vector và trục x dương.
Hai đầu mút của vector gồm:
- Tail: điểm bắt đầu.
- Head: điểm kết thúc (thường có mũi tên chỉ hướng).
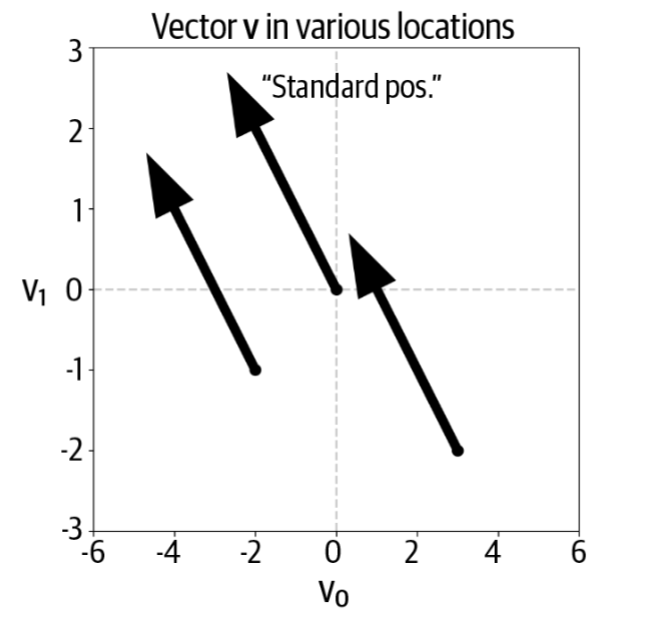
Vị trí chuẩn (Standard position)
- Một vector ở vị trí chuẩn khi điểm đầu (tail) nằm tại gốc tọa độ (0,0), và điểm đầu mũi tên (head) nằm tại tọa độ tương ứng với vector.
- Ví dụ trong hình: các mũi tên đều thể hiện cùng một vector, dù bắt đầu từ các vị trí khác nhau.
- Khi vector ở vị trí chuẩn, nó trùng với tọa độ hình học tương ứng.
Ý nghĩa của hai cách hiểu
- Hai cách hiểu đại số và hình học chỉ là hai mặt của cùng một vấn đề:
- Hình học giúp trực quan hóa, hữu ích trong vật lý, kỹ thuật (ví dụ: biểu diễn lực).
- Đại số giúp tính toán và lưu trữ, hữu ích trong khoa học dữ liệu (ví dụ: lưu chuỗi doanh số).
2. Operations on Vectors
Adding Two Vectors
- Định nghĩa:
Cộng từng phần tử tương ứng của hai vector cùng chiều. - Điều kiện:
Hai vector phải có cùng số chiều (dimensionality).
→ Không thể cộng với .
Phép trừ vector (Vector Subtraction)
- Định nghĩa:
Trừ từng phần tử tương ứng.
Cộng và trừ vector trong Python
import numpy as np
v = np.array([4,5,6])
w = np.array([10,20,30])
u = np.array([0,3,6,9])
v_plus_w = v + w # hợp lệ, cùng kích thước
u_plus_w = u + w # lỗi, khác kích thước- Lỗi “dimension mismatched” xảy ra khi số chiều khác nhau.
Ảnh hưởng của Orientation (Hướng của vector)
- Câu hỏi: Có cộng được row vector với column vector không? Ví dụ:
v = np.array([[4,5,6]]) # row vector (1x3)
w = np.array([[10,20,30]]).T # column vector (3x1)
v + wKết quả:
array([[14, 15, 16],
[24, 25, 26],
[34, 35, 36]])
- Python tự động áp dụng “broadcasting” — một quy tắc nhân bản dữ liệu để khớp kích thước mảng.
- Tuy nhiên, đây không phải là phép cộng vector theo nghĩa đại số, mà là kết quả của việc cộng một hàng với một cột.
Geometry of Vector Addition and Subtraction
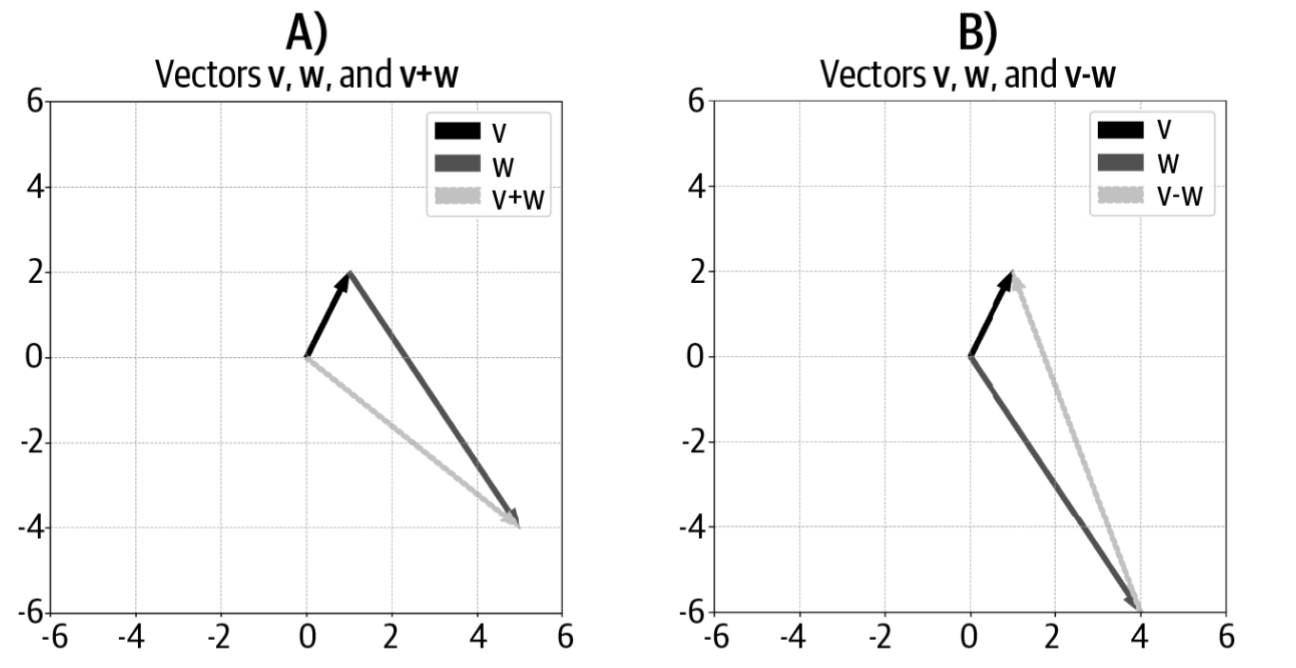
- Để cộng hai vector theo cách hình học:
- Đặt đuôi (tail) của vector thứ hai trùng với đầu (head) của vector thứ nhất.
- Vector tổng là đường nối từ đuôi của vector đầu tiên đến đầu của vector thứ hai.
- Có thể mở rộng cho nhiều vector: xếp các vector nối đuôi–đầu liên tiếp, vector tổng là đường thẳng nối từ điểm đầu tiên đến điểm cuối cùng.
Trừ vector theo hình học (Geometric Subtraction)
- Khi trừ hai vector, ta thực hiện ngược lại:
- Đặt đuôi của cả hai vector tại cùng một điểm (thường là gốc tọa độ – standard position).
- Vector hiệu là đường nối từ đầu của vector “âm” (−w) đến đầu của vector “dương” (v).
Ý nghĩa toán học và ứng dụng
- Hình học của phép trừ vector là nền tảng cho phép phân rã trực giao (orthogonal decomposition).
- Phân rã trực giao là cơ sở cho:
- Linear least squares – phương pháp bình phương tối thiểu tuyến tính.
- Ứng dụng rộng trong khoa học dữ liệu, kỹ thuật và vật lý.
Vector-Scalar Multiplication
- Scalar (vô hướng) là một số thực độc lập, không nằm trong vector hoặc ma trận (ví dụ: α, β, λ).
- Phép nhân vector–scalar: nhân từng phần tử của vector với cùng một số vô hướng.
(t-r \frac{t^T r}{r^T r})^T r = 0