Search

Bài toán tìm kiếm liên quan đến một tác nhân (agent) được cung cấp trạng thái ban đầu và trạng thái mục tiêu, sau đó trả về giải pháp để đi từ trạng thái ban đầu đến trạng thái mục tiêu. Ví dụ: Một ứng dụng chỉ đường sử dụng quy trình tìm kiếm điển hình, trong đó tác nhân (phần suy nghĩ của chương trình) nhận đầu vào là vị trí hiện tại của bạn và điểm đến mong muốn, sau đó sử dụng thuật toán tìm kiếm để đề xuất lộ trình. Tuy nhiên, có nhiều dạng bài toán tìm kiếm khác nhau, chẳng hạn như giải đố hoặc mê cung.

Trò chơi xếp số 15 (15 Puzzle)

image 4.png Việc tìm lời giải cho trò chơi xếp số 15 đòi hỏi sử dụng thuật toán tìm kiếm.

Các khái niệm quan trọng trong bài toán tìm kiếm

Tác nhân (Agent): An entity that perceives its environment and acts upon that environment.

Một thực thể nhận biết môi trường xung quanh và thực hiện hành động dựa trên môi trường đó.

Ví dụ: Trong ứng dụng chỉ đường, tác nhân có thể được mô phỏng là một chiếc xe cần quyết định hành động nào để đến đích.
Trạng thái (State): A configuration of an agent in its environment.

Một cấu hình cụ thể của một tác nhân trong môi trường.

Ví dụ, trong trò chơi xếp số 15, state là cách mà các con số được sắp xếp trên bảng tại một thời điểm nhất định.
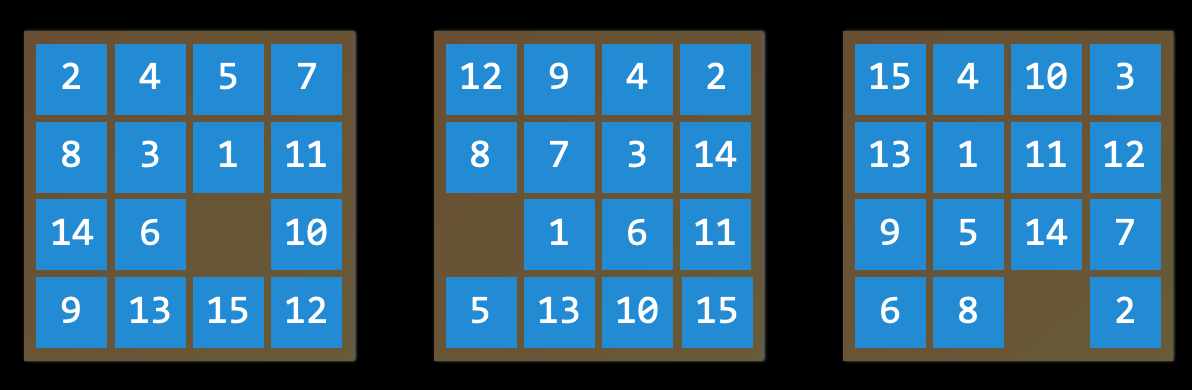
- Trạng thái ban đầu (Initial State): the state from which the search algorithm starts.
  
  Trạng thái mà thuật toán tìm kiếm bắt đầu. Trong ứng dụng chỉ đường, đây chính là vị trí hiện tại của người dùng.
Hành động (Actions): Choices that can be made in a state.

Các lựa chọn có thể thực hiện trong một trạng thái.

Chính xác hơn, hành động có thể được biểu diễn dưới dạng một hàm: với đầu vào là trạng thái s, hàm Actions(s) trả về tập hợp các hành động có thể thực hiện trong trạng thái đó.

Ví dụ, trong trò chơi xếp số 15, hành động của một trạng thái là cách mà các ô có thể trượt

4 hướng nếu ô trống ở giữa,

3 hướng nếu ô trống sát mép,

2 hướng nếu ô trống ở góc.
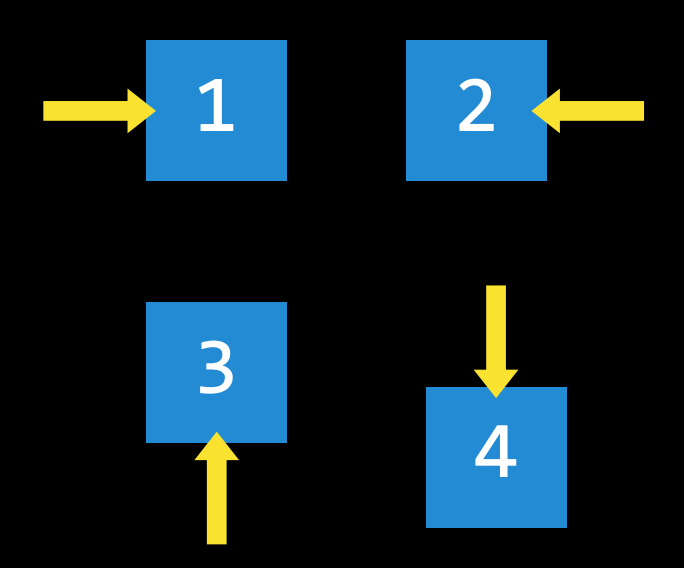
Mô hình chuyển đổi (Transition Model): A description of what state results from performing any applicable action in any state.

Mô tả trạng thái nào sẽ xuất hiện khi thực hiện một hành động trong một trạng thái cụ thể.

Mô hình chuyển đổi được định nghĩa bằng hàm: với đầu vào là trạng thái s và hành động a, hàm Results(s, a) trả về trạng thái mới sau khi thực hiện hành động a tại trạng thái s.

Ví dụ, trong trò chơi xếp số 15, nếu di chuyển một ô số (hành động a) trong một cấu hình cụ thể (trạng thái s), ta sẽ có một cấu hình mới của trò chơi (trạng thái mới).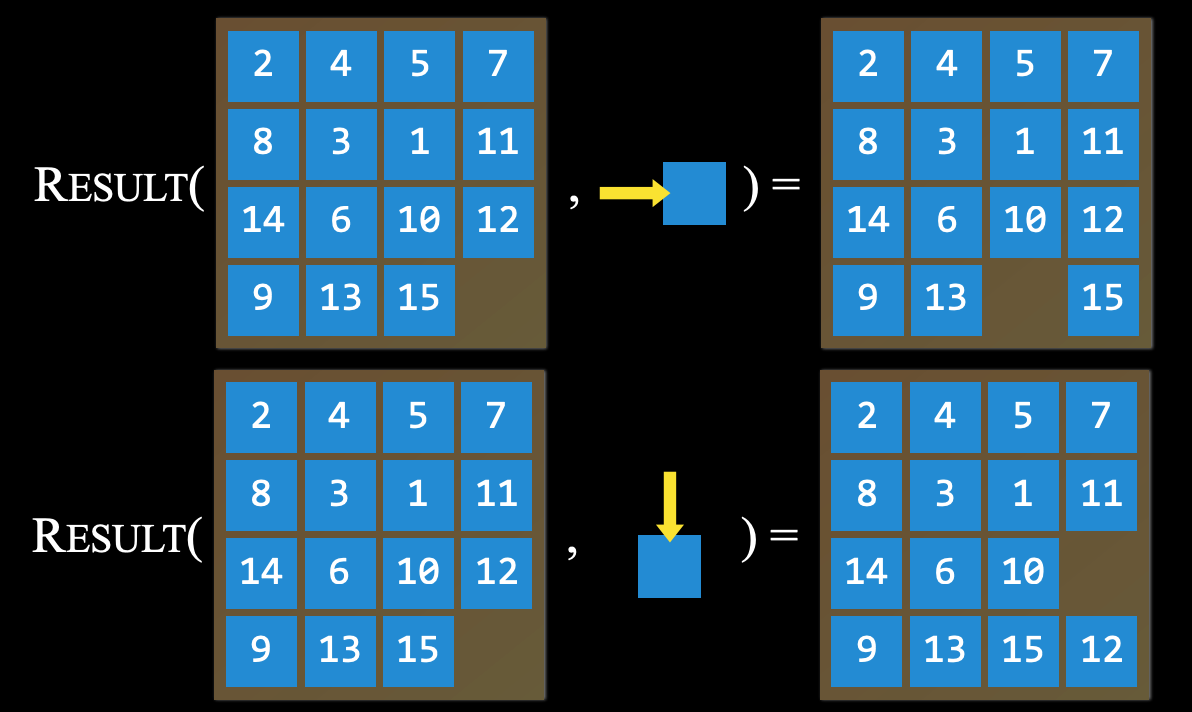
Không gian trạng thái (State Space):

Tập hợp tất cả các trạng thái có thể đạt được từ trạng thái ban đầu thông qua bất kỳ chuỗi hành động nào.

Ví dụ, trong trò chơi xếp số 15, không gian trạng thái bao gồm tất cả 16!/2 cách sắp xếp có thể có trên bảng từ bất kỳ trạng thái ban đầu nào. Không gian trạng thái có thể được biểu diễn dưới dạng một đồ thị có hướng, trong đó các trạng thái là các nút và các hành động là các mũi tên nối giữa các nút.
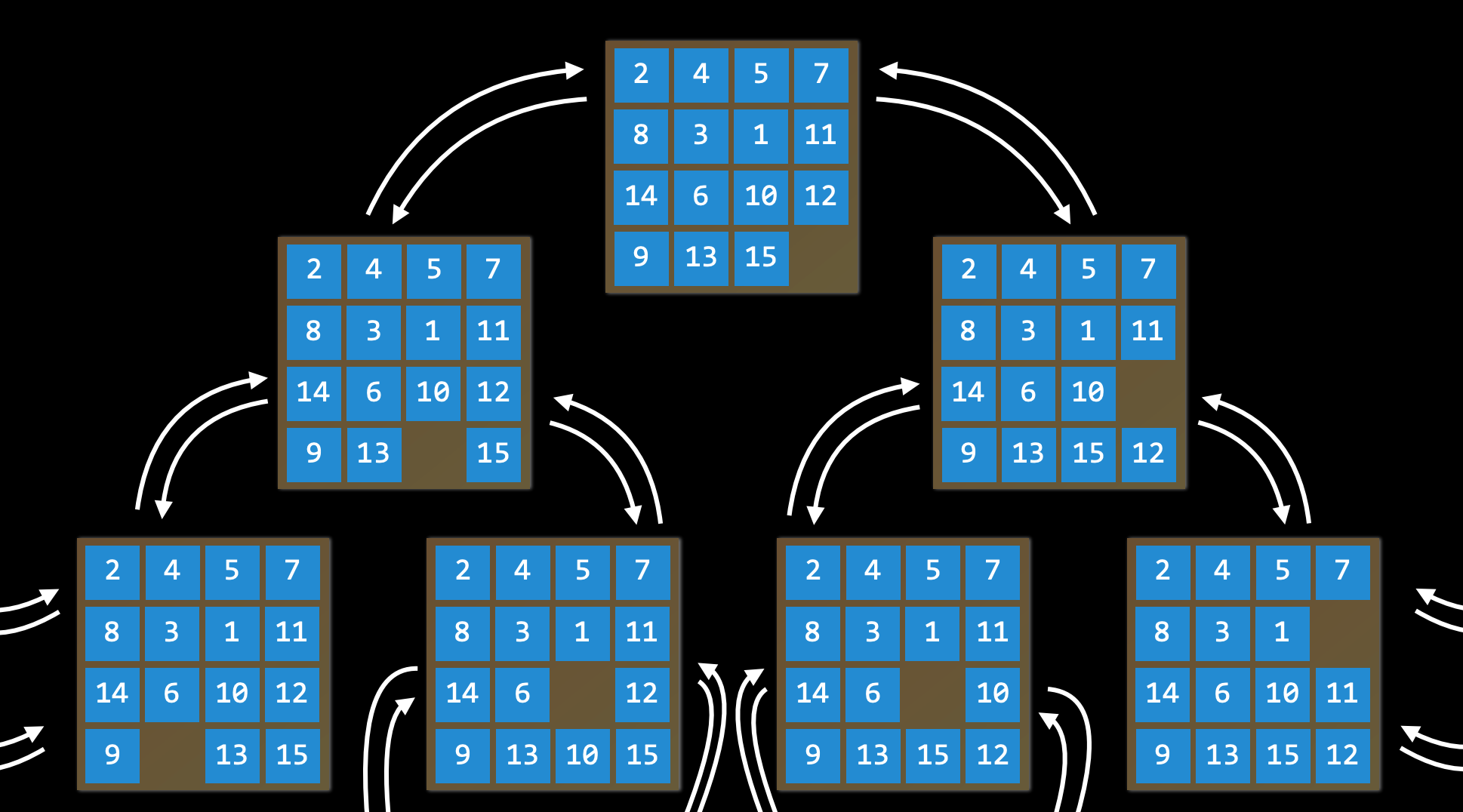
Kiểm tra mục tiêu (Goal Test):

Điều kiện xác định xem một trạng thái có phải là trạng thái mục tiêu hay không.

Ví dụ, trong ứng dụng chỉ đường, kiểm tra mục tiêu sẽ là xem vị trí hiện tại của tác nhân (xe) có trùng với điểm đến không. Nếu trùng, bài toán kết thúc. Nếu chưa, quá trình tìm kiếm tiếp tục.
Chi phí đường đi (Path Cost):

Giá trị số liên quan đến một đường đi cụ thể.

Ví dụ, ứng dụng điều hướng không chỉ đưa bạn đến đích mà còn cố gắng tối ưu hóa chi phí đường đi, tìm ra con đường nhanh nhất để bạn đến nơi.

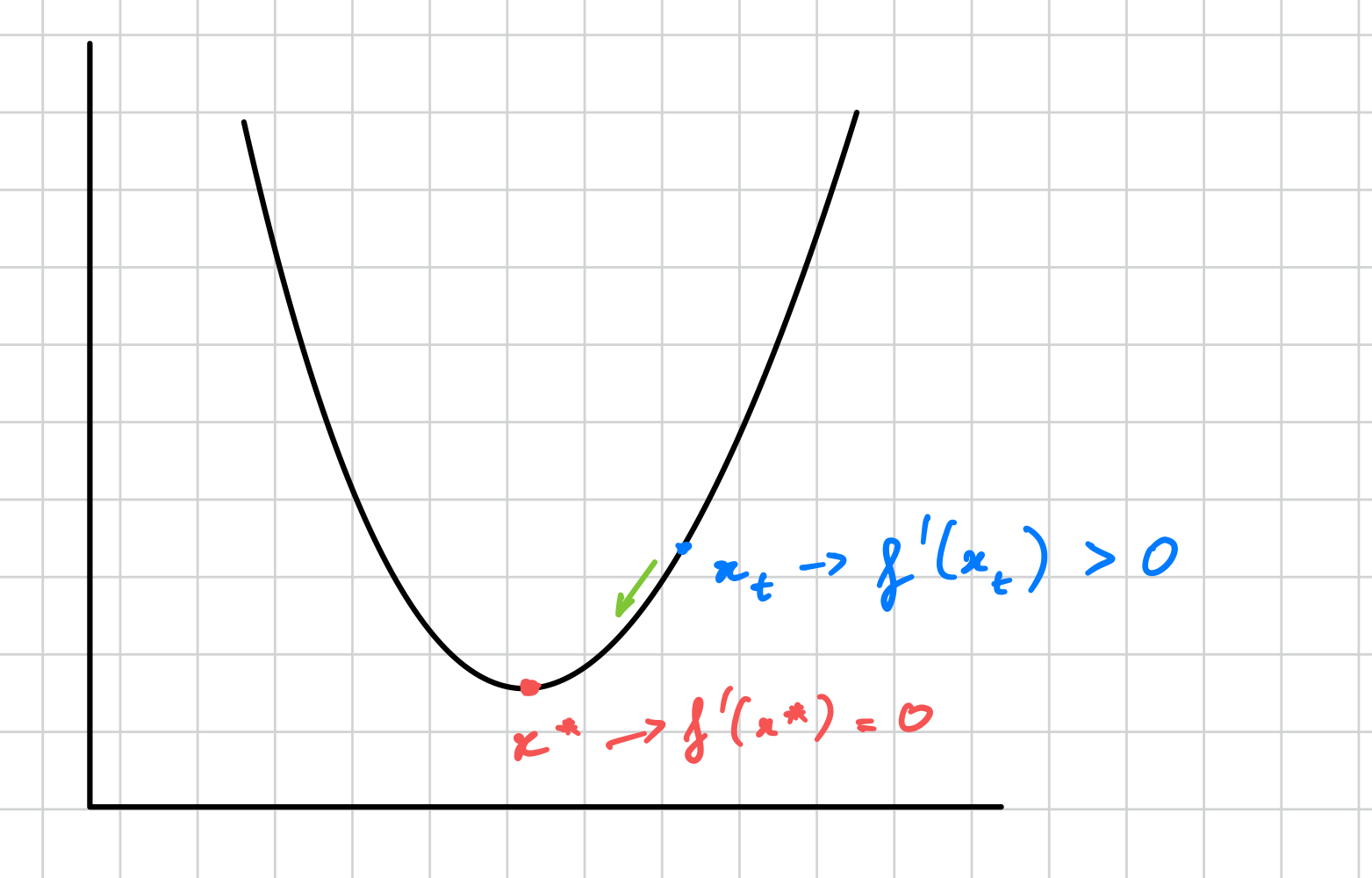
Solving Search Problems

Solution: Một chuỗi hành động dẫn từ trạng thái ban đầu đến trạng thái mục tiêu.
- Optimal Solution: Một giải pháp có tổng chi phí đường đi thấp nhất trong tất cả các giải pháp. Trong quá trình tìm kiếm, dữ liệu thường được lưu trữ trong một nút (node), một cấu trúc dữ liệu chứa các thông tin sau:
Một trạng thái (state)
Nút cha (parent node), từ đó nút hiện tại được tạo ra
Hành động (action) được áp dụng lên trạng thái của nút cha để tạo ra nút hiện tại
Chi phí đường đi (path cost) từ trạng thái ban đầu đến nút này Các nút chứa thông tin rất hữu ích cho các thuật toán tìm kiếm. Chúng chứa trạng thái, có thể kiểm tra bằng bài kiểm tra mục tiêu (goal test) để xem trạng thái đó có phải là trạng thái đích hay không. Nếu đúng, chi phí đường đi của nút có thể được so sánh với các nút khác để chọn giải pháp tối ưu. Khi một nút được chọn, do nó lưu trữ cả nút cha và hành động dẫn từ cha đến nút hiện tại, ta có thể lần theo từng bước từ trạng thái ban đầu đến nút này. Chuỗi hành động này chính là Solution (giải pháp). Tuy nhiên, các nút chỉ là một cấu trúc dữ liệu — chúng không tự tìm kiếm, mà chỉ lưu trữ thông tin. Để thực hiện việc tìm kiếm, ta sử dụng frontier, cơ chế giúp quản lý các nút. Frontier bắt đầu bằng trạng thái ban đầu và một tập rỗng các phần tử đã được khám phá. Sau đó, nó lặp lại các hành động sau cho đến khi tìm ra giải pháp:

Quy trình tìm kiếm:

Start with a frontier that contains the initial state.
Lặp lại:
1. Nếu frontier trống:
  - Dừng lại. Không có giải pháp cho bài toán.
2. Loại bỏ một nút khỏi frontier:
  - Đây là nút sẽ được xem xét.
3. Nếu nút đó chứa trạng thái mục tiêu:
  - Trả về giải pháp. Dừng lại.
4. Nếu không:
  - Mở rộng nút (tìm tất cả các nút mới có thể đạt được từ nút xem xét) và thêm các nút mới vào frontier.
  - Thêm nút hiện tại vào tập đã khám phá. Ví dụ: Tìm đường từ A đến E
Bước 1: Bắt đầu với Frontier chứa initial state. → A
Bước 2: Vì có frontier (not empty) nên tiếp tục.
Bước 3: Remove a node from the frontier. → Xóa A
Bước 4: Vì node A không phải goal state nên không return solution
Bước 5: Mở rộng nút (tìm tất cả các nút liên kết với A), trả các nút về Frontier → B
Bước 6: Xóa B
Bước 7: Thêm nút C và D
Bước 8: Remove a node from the frontier → xóa nút C
Bước 9: Thêm nút E
Bước 10: Xóa nút E:
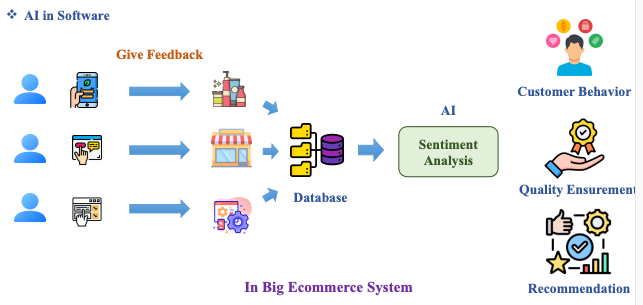
Kết luận E là solution:

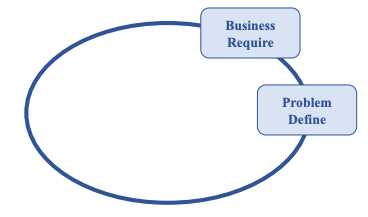
Ví dụ 2: Tìm đường từ A đến E

Bước 1: Frontier: A
Bước 2: Frontier: _ | Xét: A
Bước 3: Frontier: B
Bước 4: Frontier: _ | Xét: B
Bước 5: Frontier: A, C, D
Bước 6: Frontier: _, C, D | Xét: A
……. Bị vòng lặp ở A và nhân đôi lên nhiều khiến việc tìm giải pháp bị xa và lâu hơn dự kiến → Cách xử lý:
Nếu chúng ta đã kiểm tra node đó rồi thì không cần quay lại nữa (không thêm vào Frontier nữa)

Revised Approach

Bắt đầu với một tập Frontier trạng thái ban đầu.
Bắt đầu với một tập Explored rỗng.
Lặp lại các bước sau:
- Nếu tập Frontier rỗng, thì không có lời giải.
- Lấy ra một nút từ tập Frontier.
- Nếu nút này chứa trạng thái mục tiêu, trả về lời giải.
- Thêm nút vừa lấy vào tập Explored.
- Mở rộng nút, thêm các nút thu được vào tập Frontier nếu chúng chưa có trong tập Frontier hoặc tập Explored.

Chúng ta thấy rằng nút nào sẽ được lấy ra khỏi tập biên? Lựa chọn này có ảnh hưởng đến chất lượng lời giải và tốc độ tìm thấy lời giải đó. Có nhiều cách để quyết định xem nút nào nên được xem xét trước, trong đó hai cách phổ biến có thể được biểu diễn bằng các cấu trúc dữ liệu là ngăn xếp (stack - dùng trong tìm kiếm theo chiều sâu, DFS) và hàng đợi (queue - dùng trong tìm kiếm theo chiều rộng, BFS

Depth-First Search

Stack

Kiểu cấu trúc dữ liệu last-in first-out.

→ Kiểu Depth-First Search: Frontier có dạng cấu trúc dữ liệu Stack

Thuật toán tìm kiếm theo chiều sâu khám phá hết một hướng đi trước khi thử sang hướng khác. Trong trường hợp này, Frontier được quản lý dưới dạng cấu trúc dữ liệu ngăn xếp (stack).

LIFO: “vào sau ra trước” (last-in first-out). Sau khi các nút được thêm vào tập biên, nút đầu tiên được lấy ra để xem xét chính là nút vừa mới được thêm vào gần nhất. Cách này khiến cho thuật toán tìm kiếm sẽ đi càng sâu càng tốt theo hướng đầu tiên nó gặp, và chỉ chuyển sang các hướng còn lại khi hướng đó không còn khả năng mở rộng thêm nữa. (Một ví dụ bên ngoài bài giảng: Hãy tưởng tượng bạn đang tìm chìa khóa của mình. Với thuật toán tìm kiếm theo chiều sâu, nếu bạn quyết định bắt đầu tìm trong chiếc quần của mình, bạn sẽ tìm hết tất cả các túi trong chiếc quần trước, lục tung từng túi và kiểm tra kỹ từng vật bên trong. Bạn chỉ dừng việc tìm kiếm trong quần và chuyển sang chỗ khác khi tất cả các túi trong chiếc quần đều đã được kiểm tra kỹ càng.) Ưu điểm:

Trong trường hợp tốt nhất, thuật toán này là nhanh nhất. Nếu thuật toán “may mắn” luôn chọn đúng con đường dẫn tới lời giải (một cách ngẫu nhiên), tìm kiếm theo chiều sâu sẽ tốn thời gian ngắn nhất để tìm ra lời giải. Nhược điểm:
Lời giải tìm được có thể không phải là lời giải tối ưu nhất.
Trong trường hợp xấu nhất, thuật toán này sẽ phải thử từng con đường khả thi trước khi tìm ra lời giải, do đó mất thời gian lâu nhất có thể để đạt được lời giải. Ví dụ về code:

# Định nghĩa hàm lấy một nút ra khỏi tập biên và trả về nút đó.
def remove(self):
    # Dừng tìm kiếm nếu tập biên rỗng, bởi vì điều này có nghĩa không tồn tại lời giải.
    if self.empty():
        raise Exception("empty frontier")
    else:
        # Lưu nút cuối cùng trong danh sách (là nút vừa mới được thêm vào)
        node = self.frontier[-1]
        # Giữ lại tất cả các nút trong danh sách ngoại trừ nút cuối cùng (tức loại bỏ nút cuối)
        self.frontier = self.frontier[:-1]
        return node

Breadth-First Search

Tìm kiếm theo chiều rộng (BFS) là thuật toán ngược lại với tìm kiếm theo chiều sâu (DFS). Thuật toán tìm kiếm theo chiều rộng sẽ đi theo nhiều hướng cùng một lúc, thực hiện một bước ở mỗi hướng có thể đi trước khi thực hiện bước thứ hai ở mỗi hướng. Trong trường hợp này, biên giới (frontier) được quản lý như một cấu trúc dữ liệu hàng đợi. Điều bạn cần nhớ là “đến trước sẽ được phục vụ trước” (first-in first-out). Trong trường hợp này, tất cả các nút mới sẽ được xếp vào hàng đợi, và các nút được xem xét dựa trên thứ tự mà chúng được thêm vào (đến trước sẽ được phục vụ trước!). Điều này dẫn đến một thuật toán tìm kiếm mà trong đó một bước được thực hiện theo mỗi hướng có thể đi trước khi thực hiện bước thứ hai ở bất kỳ hướng nào. (Một ví dụ từ ngoài bài giảng: giả sử bạn đang tìm chìa khóa của mình. Trong trường hợp này, nếu bạn bắt đầu với chiếc quần của mình, bạn sẽ kiểm tra túi phải trước. Sau đó, thay vì kiểm tra túi trái, bạn sẽ kiểm tra một ngăn kéo. Sau đó, bạn kiểm tra trên bàn. Và cứ thế, bạn sẽ kiểm tra tất cả các vị trí bạn nghĩ đến. Chỉ sau khi đã kiểm tra hết tất cả các vị trí, bạn mới quay lại chiếc quần và kiểm tra túi còn lại.) Ưu điểm: Thuật toán này đảm bảo tìm ra giải pháp tối ưu. Nhược điểm: Thuật toán này gần như chắc chắn sẽ mất nhiều thời gian hơn so với thời gian tối thiểu để chạy. Trong trường hợp xấu nhất, thuật toán này mất nhiều thời gian nhất để chạy. Ví dụ mã code:

# Định nghĩa hàm loại bỏ một nút khỏi biên giới và trả về nó.
def remove(self):
    # Dừng tìm kiếm nếu biên giới rỗng, vì điều này có nghĩa là không có giải pháp.
    if self.empty():
        raise Exception("Frontier empty")
    else:
        # Lưu trữ phần tử cũ nhất trong danh sách (đã được thêm vào đầu tiên)
        node = self.frontier[0]
        # Lưu trữ tất cả các phần tử trong danh sách ngoại trừ phần tử đầu tiên (tức là loại bỏ nút đầu tiên)
        self.frontier = self.frontier[1:]
        return node

Greedy Best-First Search

Tìm kiếm theo chiều rộng và tìm kiếm theo chiều sâu là cả hai thuật toán tìm kiếm không có thông tin (uninformed search algorithms). Điều này có nghĩa là các thuật toán này không sử dụng bất kỳ kiến thức nào về bài toán mà chúng không thu được thông qua quá trình khám phá của chính chúng. Tuy nhiên, trong nhiều trường hợp, một số kiến thức về bài toán thực tế là có sẵn. Ví dụ, khi một người giải mê cung đến một ngã rẽ, người đó có thể nhìn thấy hướng nào đi về phía giải pháp và hướng nào không. AI cũng có thể làm điều tương tự. Một loại thuật toán sử dụng kiến thức bổ sung để cố gắng cải thiện hiệu suất của nó được gọi là thuật toán tìm kiếm có thông tin (informed search algorithm). Greedy Best-First Search: mở rộng nút gần nhất với mục tiêu, được xác định bởi một hàm đánh giá h(n). Như tên gọi của nó, hàm này ước tính mức độ gần gũi của nút tiếp theo với mục tiêu, nhưng có thể bị sai. Hiệu quả của thuật toán tìm kiếm tham lam tốt nhất phụ thuộc vào độ chính xác của hàm đánh giá. Ví dụ, trong một mê cung, một thuật toán có thể sử dụng một hàm đánh giá dựa trên khoảng cách Manhattan giữa các nút có thể đến và điểm kết thúc của mê cung. Khoảng cách Manhattan bỏ qua các bức tường và đếm số bước lên, xuống hoặc sang hai bên cần thiết để đi từ một vị trí đến vị trí mục tiêu. Đây là một ước lượng đơn giản có thể được rút ra từ tọa độ (x, y) của vị trí hiện tại và vị trí mục tiêu. 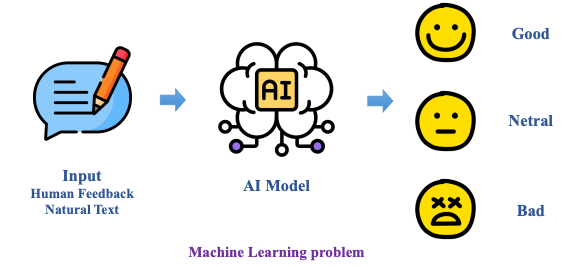Tuy nhiên, cần nhấn mạnh rằng, như với bất kỳ hàm đánh giá nào, nó có thể sai và dẫn đến thuật toán đi vào một con đường chậm hơn so với những gì nó sẽ làm nếu không sử dụng hàm đánh giá. Có thể thuật toán tìm kiếm không có thông tin sẽ đưa ra một giải pháp tốt hơn nhanh hơn, nhưng khả năng này ít có hơn so với một thuật toán có thông tin.

*A Search**

Là sự phát triển của thuật toán tìm kiếm tham lam tốt nhất, tìm kiếm A* không chỉ xem xét h(n), chi phí ước tính từ vị trí hiện tại đến mục tiêu, mà còn xem xét g(n), chi phí tích lũy cho đến vị trí hiện tại. Bằng cách kết hợp cả hai giá trị này, thuật toán có một cách chính xác hơn để xác định chi phí của giải pháp và tối ưu hóa các lựa chọn của mình trong quá trình tìm kiếm. Thuật toán theo dõi (chi phí của con đường cho đến nay + chi phí ước tính đến mục tiêu), và khi chi phí này vượt quá chi phí ước tính của một lựa chọn trước đó, thuật toán sẽ bỏ qua con đường hiện tại và quay lại lựa chọn trước đó, ngăn chặn việc đi xuống một con đường dài và không hiệu quả mà h(n) sai lầm đã đánh dấu là tốt nhất. 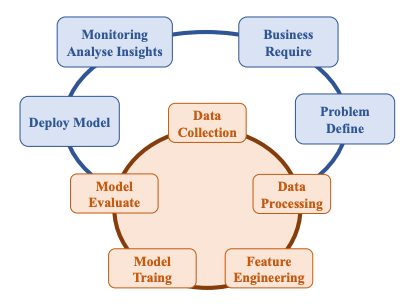Tuy nhiên, một lần nữa, vì thuật toán này cũng dựa vào một hàm đánh giá, nó sẽ tốt như hàm đánh giá mà nó sử dụng. Có thể trong một số tình huống, nó sẽ kém hiệu quả hơn tìm kiếm tham lam tốt nhất hoặc thậm chí các thuật toán không có thông tin. Để tìm kiếm A* là tối ưu, hàm đánh giá h(n) cần phải:

h(n) is admissible (never overestimates the true cost), and
h(n) is consistent (for every node n and successor n’ with step cost c, h(n) ≤ h(n’) + c)

Adversarial Search

Trong khi trước đó, chúng ta đã thảo luận về các thuật toán cần tìm một câu trả lời cho một câu hỏi, trong Adversarial Search, thuật toán đối mặt với một đối thủ cố gắng đạt được mục tiêu ngược lại. Thường thì AI sử dụng Adversarial Search trong các trò chơi, chẳng hạn như cờ ca rô.

Minimax

Là một loại thuật toán trong tìm kiếm đối kháng, Minimax đại diện cho điều kiện thắng lợi là (-1) cho một bên và (+1) cho bên kia. Các hành động tiếp theo sẽ được điều khiển bởi các điều kiện này, với bên muốn giảm điểm cố gắng đạt điểm thấp nhất, và bên muốn tăng điểm cố gắng đạt điểm cao nhất. Biểu diễn AI Cờ ca rô:

S₀: Trạng thái ban đầu (trong trường hợp của chúng ta, một bảng 3x3 trống)
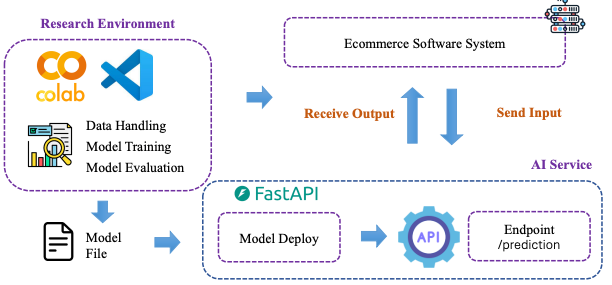
Players(s): Một hàm trả về lượt của người chơi cho trạng thái s.
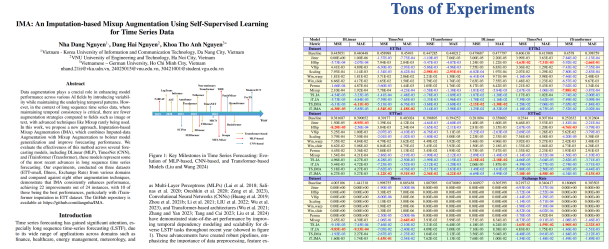
Actions(s): Một hàm trả về tất cả các nước đi hợp lệ trong trạng thái s (các ô nào còn trống trên bảng).
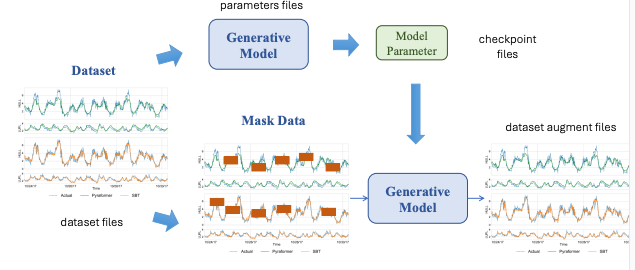
Result(s, a): Một hàm trả về trạng thái mới, sau khi thực hiện hành động a trên trạng thái s (thực hiện một nước đi trong trò chơi).
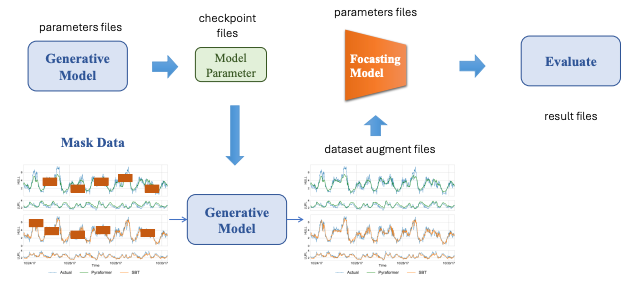
Terminal(s): Một hàm kiểm tra xem trạng thái s có phải là bước cuối cùng trong trò chơi không, tức là ai đó đã thắng hoặc có hòa không. Trả về True nếu trò chơi kết thúc, False nếu không.
Utility(s): Một hàm trả về giá trị tiện ích của trạng thái s: -1, 0, hoặc 1.

Cách hoạt động của thuật toán: Thuật toán này mô phỏng tất cả các trò chơi có thể xảy ra bắt đầu từ trạng thái hiện tại cho đến khi đạt được trạng thái kết thúc. Mỗi trạng thái kết thúc được gán giá trị là (-1), 0, hoặc (+1). Thuật toán Minimax trong Cờ Ca Rô: Biết được dựa trên trạng thái của lượt chơi, thuật toán có thể xác định liệu người chơi hiện tại, khi chơi tối ưu, sẽ chọn hành động dẫn đến trạng thái có giá trị thấp hơn hay cao hơn. Theo cách này, thay phiên giữa việc giảm thiểu và tối đa hóa, thuật toán tạo ra các giá trị cho trạng thái có thể xảy ra từ mỗi hành động có thể. Để đưa ra một ví dụ cụ thể hơn, chúng ta có thể tưởng tượng rằng người chơi tối ưu sẽ hỏi trong mỗi lượt chơi: “Nếu tôi thực hiện hành động này, một trạng thái mới sẽ được tạo ra. Nếu người chơi giảm thiểu chơi tối ưu, hành động nào mà người đó có thể thực hiện để đưa giá trị về thấp nhất?” Tuy nhiên, để trả lời câu hỏi này, người chơi tối ưu phải hỏi lại: “Để biết người chơi giảm thiểu sẽ làm gì, tôi cần mô phỏng cùng một quá trình trong đầu người chơi giảm thiểu: người chơi giảm thiểu sẽ cố gắng hỏi: ‘Nếu tôi thực hiện hành động này, hành động nào mà người chơi tối ưu có thể thực hiện để đưa giá trị về cao nhất?‘” Đây là một quá trình đệ quy, và nó có thể khó hiểu; nhìn vào mã giả dưới đây có thể giúp ích. Cuối cùng, qua quá trình suy luận đệ quy này, người chơi tối ưu tạo ra các giá trị cho mỗi trạng thái có thể xảy ra từ tất cả các hành động có thể từ trạng thái hiện tại. Sau khi có các giá trị này, người chơi tối ưu sẽ chọn giá trị cao nhất.

An Hoai Thai's Notes

Trong bài này

Các thuật toán Search