Table of Content
Important
Tham khảo
I. Vector and Matrix
System of Linear Equations
Hệ phương trình tuyến tính mô tả mối quan hệ giữa đặc trưng (Features) và nhãn (Label) thông qua một mô hình tuyến tính. Trong ví dụ này, chúng ta dự đoán Sales dựa trên chi phí quảng cáo ở các kênh TV, Radio, và Newspaper. Mô hình tuyến tính Phương trình tổng quát: Trong đó:
- a₁, a₂, a₃: hệ số ảnh hưởng của từng kênh quảng cáo
- b: hằng số (intercept), ở đây giả sử b = 0 để đơn giản hóa Bảng dữ liệu mẫu: |TV|Radio|Newspaper|Sales| |---|---|---|---| |230.1|37.8|69.2|22.1| |44.5|39.3|45.1|10.4| |17.2|45.9|69.3|12.0| Dạng hệ phương trình Từ dữ liệu, ta có hệ: a₁T₁ + a₂R₁ + a₃N₁ = S₁ a₁T₂ + a₂R₂ + a₃N₂ = S₂ a₁T₃ + a₂R₃ + a₃N₃ = S₃ Trong đó:
- Tᵢ: giá trị quảng cáo TV ở dòng i
- Rᵢ: giá trị quảng cáo Radio ở dòng i
- Nᵢ: giá trị quảng cáo Newspaper ở dòng i
- Sᵢ: doanh số (Sales) ở dòng i
Biểu diễn ma trận Hệ trên được viết gọn lại: a₁[T₁, T₂, T₃]ᵀ + a₂[R₁, R₂, R₃]ᵀ + a₃[N₁, N₂, N₃]ᵀ = [S₁, S₂, S₃]ᵀ Hoặc: A · x = b Với:
-
A = ma trận đặc trưng
-
x = vector hệ số
-
b = vector kết quả [S₁, S₂, S₃]ᵀ
 ⇒ Việc viết dưới dạng ma trận giúp ta có thể giải hệ nhanh bằng các phương pháp đại số tuyến tính (nghịch đảo ma trận, phương pháp khử Gauss, hoặc dùng NumPy).
⇒ Việc viết dưới dạng ma trận giúp ta có thể giải hệ nhanh bằng các phương pháp đại số tuyến tính (nghịch đảo ma trận, phương pháp khử Gauss, hoặc dùng NumPy).
Các cách giải
-
Phương pháp Cramer
Áp dụng cho hệ có số phương trình = số ẩn , ma trận khả nghịch.
Công thức:
- : ma trận thay cột thứ của bằng vector .
- Thích hợp cho hệ nhỏ, nhưng tính determinant tốn kém khi lớn.
-
Khử Gauss (Gaussian Elimination)
Biến đổi ma trận mở rộng thành dạng tam giác trên, sau đó giải bằng thế lùi.
Quy trình:
-
Dùng phép biến đổi sơ cấp để đưa về dạng bậc thang.
-
Giải từ phương trình cuối cùng lên trên.
Ưu điểm: tính toán đơn giản, áp dụng được cho hệ vừa và lớn.
Nhược điểm: dễ sinh sai số số học khi ma trận gần suy biến.
-
-
Phân rã ma trận
-
LU Decomposition:
Với : ma trận tam giác dưới, : tam giác trên. Giải hệ bằng 2 bước thế tiến & lùi.
-
Cholesky Decomposition:
-
I.1. Introduction
Vector
- là một số tự nhiên
- ℝ là tập hợp các số thực
- là vector có độ dài , mỗi phần tử là số thực
- Ký hiệu: Vector là ma trận 1 cột, là khối xây dựng cơ bản của ma trận. Khi học máy, vector thường biểu diễn đặc trưng hoặc trọng số.
Matrix
- Ma trận có hình chữ nhật (hàng × cột)
- Có hàng và cột
- Dùng chữ cái in hoa để biểu diễn
- Ký hiệu: Trong học máy, ma trận thường biểu diễn tập dữ liệu: mỗi hàng là 1 mẫu (sample), mỗi cột là 1 đặc trưng (feature).
I.2. Vector Operations
Vector Addition – Cộng hai vector
Cho hai vector: Phép cộng được định nghĩa: Code Python:
def add_vectors(vector1, vector2):
'''
Add corresponding elements between two vectors
vector1 and vector2 are lists
'''
return [v1 + v2 for v1, v2 in zip(vector1, vector2)]NumPy:
import numpy as np
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
print("data x \n", x)
print("data y \n", y)
# Cách 1: toán tử +
print("method 1 \n", x + y)
# Cách 2: hàm np.add
print("method 2 \n", np.add(x, y))Output:
data x
[1 2 3 4]
data y
[5 6 7 8]
method 1
[ 6 8 10 12]
method 2
[ 6 8 10 12]NumPy tự động vector hóa các toán tử, giúp xử lý nhanh trên mảng lớn mà không cần vòng lặp.
I.3. Matrix Operations
Matrix-matrix multiplication
Cho hai ma trận:
-
Tích ma trận:
Định nghĩa phần tử kết quả
Phần tử trong ma trận kết quả được tính theo công thức:
Tức là: hàng thứ i của nhân từng phần tử tương ứng với cột thứ j của .
Biểu diễn tổng quát
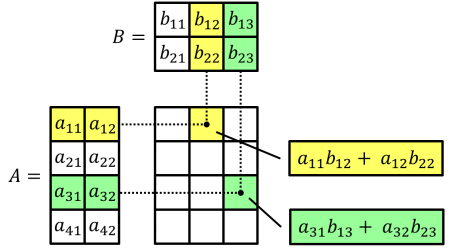 Số cột của ma trận đầu tiên (A) phải bằng số hàng của ma trận thứ hai (B). Nếu không, phép nhân không xác định.
Cài đặt Python:
Số cột của ma trận đầu tiên (A) phải bằng số hàng của ma trận thứ hai (B). Nếu không, phép nhân không xác định.
Cài đặt Python:
def matrix_multiplication(matrix1, matrix2):
'''
Multiply matrix1 (m x n) with matrix2 (n x d)
'''
matrix1_nrows = len(matrix1)
matrix1_ncols = len(matrix1[0])
matrix2_nrows = len(matrix2)
matrix2_ncols = len(matrix2[0])
# Khởi tạo ma trận kết quả kích thước m x d
result = [[0] * matrix2_ncols for _ in range(matrix1_nrows)]
for i in range(matrix1_nrows):
for j in range(matrix2_ncols):
for k in range(matrix2_nrows):
result[i][j] += matrix1[i][k] * matrix2[k][j]
return resultKiểm tra:
matrix1 = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
matrix2 = [
[1, 1, 2, 1],
[1, 2, 1, 1],
[1, 1, 2, 2]
]
result = matrix_multiplication(matrix1, matrix2)
for row in result:
print(row)Kết quả:
[6, 8, 7, 9]
[15, 20, 19, 21]
[24, 32, 31, 33]Cài đặt NumPy:
import numpy as np
X = np.array([[1, 2],
[3, 4]])
Y = np.array([[2, 3],
[2, 1]])Lưu ý phân biệt:
- Thứ tự hàng × cột rất quan trọng
- Trong học sâu, cần chú ý thứ tự khi nhân weight matrix × input

Transpose
Other Hadamard operations
argmin and argmax
Khi làm việc với vector hoặc ma trận, đôi khi ta không cần biết giá trị lớn nhất/nhỏ nhất, mà cần biết vị trí (index) của giá trị đó.
- argmin: trả về chỉ số của phần tử nhỏ nhất
- argmax: trả về chỉ số của phần tử lớn nhất Ví dụ: Tìm index nhỏ nhất:
import numpy as np
x = np.array([4, 7, 1, 5])
result = np.argmin(x)
print(result) # Output: 2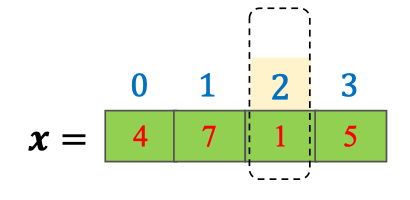 → Phần tử nhỏ nhất là
→ Phần tử nhỏ nhất là 1, nằm ở vị trí chỉ số 2
Tìm index lớn nhất:
result = np.argmax(x)
print(result) # Output: 1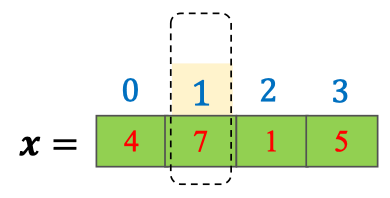 → Phần tử lớn nhất là
→ Phần tử lớn nhất là 7, nằm ở vị trí chỉ số 1
III. Cosine Similarity
III.1. Dot Product
Tích vô hướng (dot product) là phép toán cơ bản giữa hai vector, trả về một số thực thể hiện mức “thẳng hàng” giữa chúng. Nó cũng chính là độ dài hình chiếu của một vector này lên một vector khác (nếu đã chuẩn hóa). Ví dụ đơn giản: Giả sử bạn có một học sinh được đánh giá qua 3 kỹ năng:
| Kỹ năng | Điểm (x) | Trọng số (w) |
|---|---|---|
| Kỹ năng đọc | 8 | 0.2 |
| Kỹ năng viết | 6 | 0.3 |
| Kỹ năng tính toán | 9 | 0.5 |
| Tổng điểm trung bình có trọng số: | ||
| Đây chính là tích vô hướng giữa 2 vector: | ||
| ⇒ Tích vô hướng cũng chính là điểm trung bình có trọng số. |
Dạng cơ bản – Chiếu lên trục tọa độ
Cho:
-
Tích vô hướng:
Khi chiếu lên trục cơ sở chuẩn như , tích vô hướng chính là tọa độ.
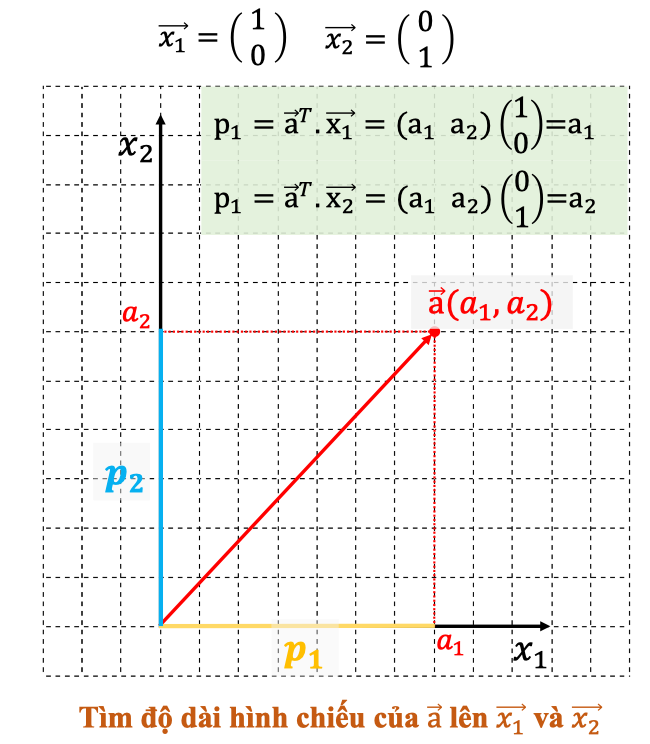
Dạng tổng quát – Chiếu lên vector bất kỳ
Cho hai vector bất kỳ:
-
Với vector , ta tính:
Nếu đã được chuẩn hóa, chính là độ dài hình chiếu của lên chúng.
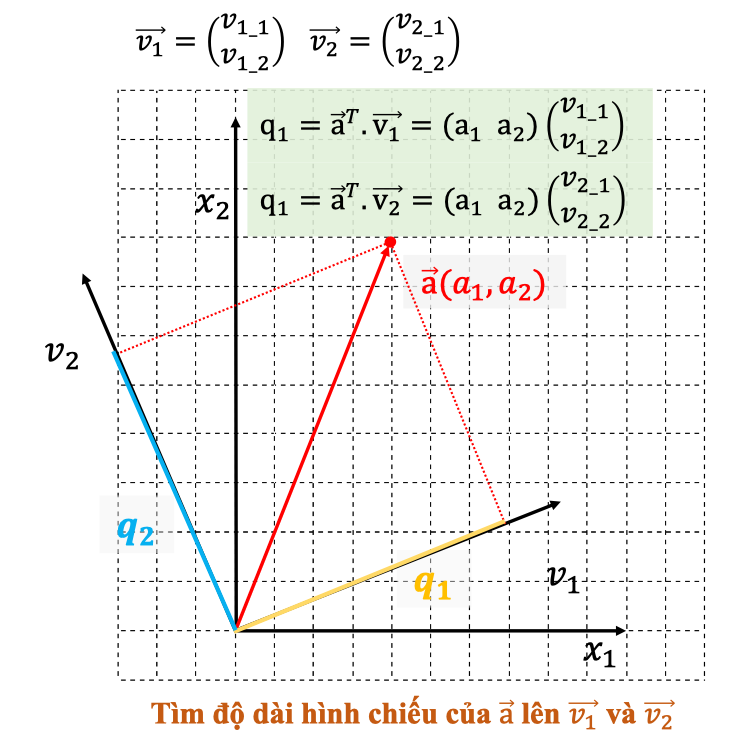
Ý nghĩa hình học của dot product
Với hai vector , công thức:
- Nếu → dot product lớn nhất
- Nếu → dot product = 0 (vuông góc)
- Nếu → dot product âm Tích vô hướng giúp kiểm tra hướng (cùng chiều hay ngược chiều) và đo khoảng cách góc (nền tảng của cosine similarity).
Tính chất hình học
Nhân vô hướng và nhân vô hướng với vô hướng
Cho:
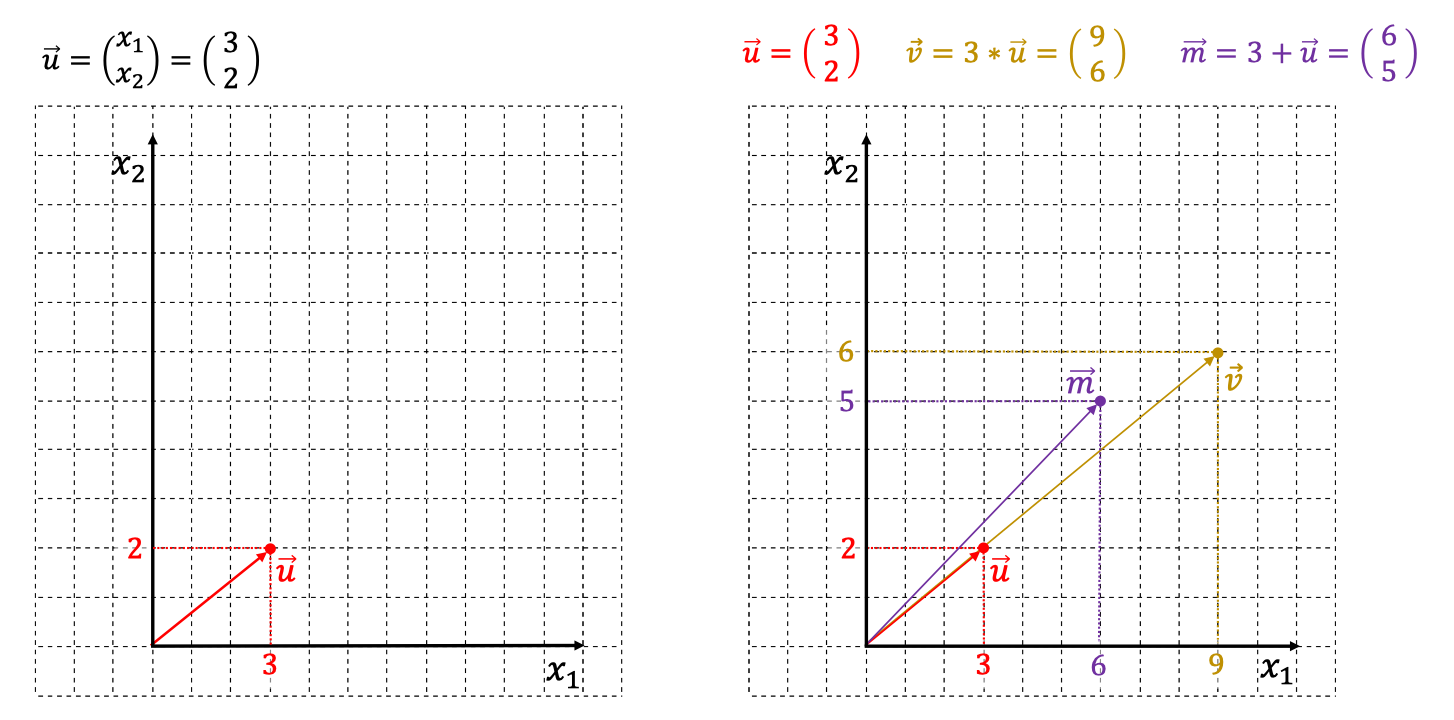 Màu đỏ: Phép nhân vô hướng giữ nguyên hướng, chỉ làm thay đổi độ dài.
Màu tím: Phép cộng làm thay đổi góc.
Màu đỏ: Phép nhân vô hướng giữ nguyên hướng, chỉ làm thay đổi độ dài.
Màu tím: Phép cộng làm thay đổi góc.
Ví dụ
Trong ví dụ này, ta sẽ dùng cả đại số tuyến tính và hình học để tính tích vô hướng giữa hai vector: Định nghĩa toán học:
- Algebra (đại số):
- Geometry (hình học):
Trong đó, , nên:
Tính độ dài:
Kết quả:
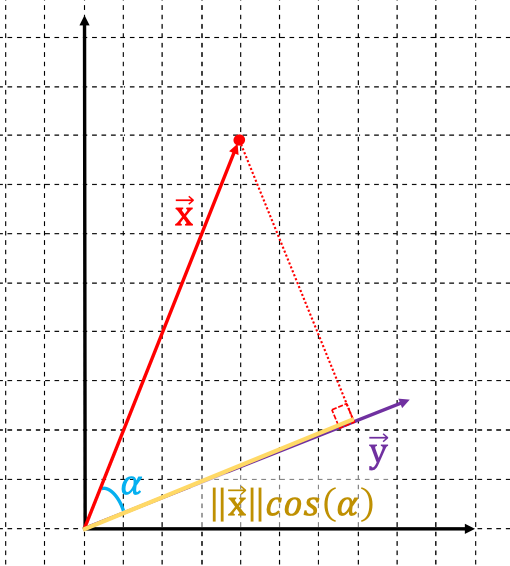
Cài đặt bằng Python: Phép tính theo đại số
import numpy as np
x = np.array([0, 5])
y = np.array([3, 3])
dproduct = np.dot(x, y)
print(dproduct) # Kết quả: 15Phép tính theo hình học
x_length = np.linalg.norm(x)
y_length = np.linalg.norm(y)
cos_xy = np.cos(np.pi / 4) # góc 45 độ
dproduct = x_length * y_length * cos_xy
print(dproduct) # Kết quả: ~15.0III.2. Cosine Similarity
Cosine similarity (cs) là độ đo phổ biến để so sánh mức độ tương đồng giữa hai vector, đặc biệt trong xử lý ngôn ngữ, truy xuất thông tin, và học máy.
Định nghĩa
Cho hai vector :
Tính chất
Property 1 – Bất biến theo scale: Chứng minh: Khi hai vector được nhân với hệ số dương, hướng không đổi, nên cosine không đổi.
Property 2 – Không bất biến theo dịch chuyển: Thêm hằng số vào các phần tử làm thay đổi góc, vì thay đổi hướng tương đối.
Ví dụ: Cho: Tính cs(x, y): Kiểm tra tính chất 1: nhân hệ số Tính: