8. Matrix Inverse

1. The Matrix Inverse

Định nghĩa: Nghịch đảo của ma trận $A$ là một ma trận khác $A^{-1}$ sao cho:

$$A^{-1}A=I$$

Trong đó $I$ là Ma trận đơn vị (identity matrix)

2. Các loại ma trận nghịch đảo và điều kiện khả nghịch

Types of Inverses and Conditions for Invertibility Không phải mọi ma trận lúc nào đều cũng có thể nghịch đảo.

Có ba loại nghịch đảo khác nhau với các điều kiện khả nghịch khác nhau.

---

2.1. Nghịch đảo đầy đủ (Full inverse)

Định nghĩa:

$$A^{-1}A=A{A}^{-1}=I$$

Có hai điều kiện để một ma trận có nghịch đảo đầy đủ:

1. Ma trận phải vuông.
2. Ma trận phải có hạng đầy đủ (full-rank) Mọi ma trận vuông có hạng đầy đủ đều có nghịch đảo, và mọi ma trận có nghịch đảo đầy đủ đều vuông và có hạng đầy đủ. Ở đây, dùng thuật ngữ nghịch đảo đầy đủ để phân biệt với hai khả năng tiếp theo; thông thường, nghịch đảo đầy đủ gọi đơn giản là nghịch đảo.

---

2.2. Nghịch đảo một phía (One_sided inverse)

Một nghịch đảo một phía có thể biến một ma trận hình chữ nhật thành ma trận đơn vị, nhưng chỉ hoạt động với một thứ tự nhân ma trận duy nhất.

• Cụ thể, một ma trận cao $T$ có thể có nghịch đảo trái (left-inverse), nghĩa là:

$$LT=I\text{nhưng}TL\ne I.$$

• Một ma trận rộng $W$ có thể có nghịch đảo phải (right-inverse), nghĩa là:

$$WR=I\text{nhưng}RW\ne I$$

Một ma trận không vuông chỉ có nghịch đảo một phía nếu nó có hạng tối đa:

• Ma trận cao có nghịch đảo trái nếu nó có hạng bằng số cột (full column rank).
• Ma trận rộng có nghịch đảo phải nếu nó có hạng bằng số hàng (full row rank).

---

2.3. Giả nghịch đảo (Pseudoinverse)

Mọi ma trận đều có giả nghịch đảo, bất kể hình dạng hay hạng.

• Nếu ma trận vuông và hạng đầy đủ, giả nghịch đảo của nó chính là nghịch đảo đầy đủ.
• Nếu ma trận không vuông nhưng có hạng tối đa, giả nghịch đảo sẽ bằng với nghịch đảo một phía (nghĩa là nghịch đảo trái đối với ma trận cao, hoặc nghịch đảo phải đối với ma trận rộng).
• Nếu ma trận bị giảm hạng (không full-rank), nó vẫn có giả nghịch đảo. Trong trường hợp này, giả nghịch đảo sẽ biến đổi ma trận suy biến thành một ma trận khác “gần giống” với ma trận đơn vị, nhưng không hoàn toàn bằng ma trận đơn vị.

---

3. Computing the Inverse

Nhắc lại, nghịch đảo của mộ số vô hướng: ta lấy phân số nghịch đảo: Ví dụ: nghịch đảo của số $3$ là $1/3$, tức là $3^{-1}$. Như vậy: $3\times 3^{-1}=1$

Từ lập luận này, có thể nghĩ rằng nghịch đảo ma trận cũng được tính bằng cách nghịch đảo từng phần tử:

$${\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]}^{-1}\stackrel{?}{=}\left[\begin{array}{cc}1/a& 1/b\\ 1/c& 1/d\end{array}\right]$$

---

Nhưng đây là cách làm sai! Nếu ta nhân ma trận gốc với ma trận chứa các phần tử đã nghịch đảo, kết quả là:

$$\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{cc}1/a& 1/b\\ 1/c& 1/d\end{array}\right]=\left[\begin{array}{cc}1+b/c& a/b+b/d\\ c/a+d/c& 1+c/b\end{array}\right]$$

Đây là một phép nhân ma trận hợp lệ, nhưng kết quả không phải ma trận đơn vị.
Điều đó chứng minh rằng: nghịch đảo từng phần tử ≠ nghịch đảo ma trận.

---

3.1. Công thức nghịch đảo cho ma trận 2×2 (Inverse of a 2×2 Matrix)

Để tính nghịch đảo của ma trận 2×2:

• Hoán đổi hai phần tử trên đường chéo chính.
• Đổi dấu hai phần tử ngoài đường chéo.
• Chia toàn bộ ma trận cho định thực $\det (A)=ad-bc$

---

Quan sát:

$$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$$ $$A^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]$$

Kiểm chứng:

$$A{A}^{-1}=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]=\frac{1}{ad-bc}\left[\begin{array}{cc}ad-bc& 0\\ 0& ad-bc\end{array}\right]=I$$

Tại sao người ta lại nghĩ ra được công thức này?

Ví dụ:

---

3.3. Nghịch đảo của bất kỳ ma trận vuông đầy đủ hạng nào

Inverting Any Square Full-Rank Matrix

Thuật toán đầy đủ để nghịch đảo một ma trận khả nghịch rất dài và tẻ nhạt, và chắc chắn sẽ không bao giờ cần dùng nó trong các ứng dụng thực tế → Thay vào đó, sẽ dùng np.linalg.inv hoặc các hàm khác gọi đến inv.

Mặt khác, việc cài đặt thuật toán này trong Python lại là một cơ hội tuyệt vời để rèn luyện kỹ năng chuyển đổi một thuật toán – được mô tả bằng công thức và tiếng Anh – sang mã Python. Vì vậy, ở đâ giải thích cách hoạt động của thuật toán mà không đưa code sẵn.

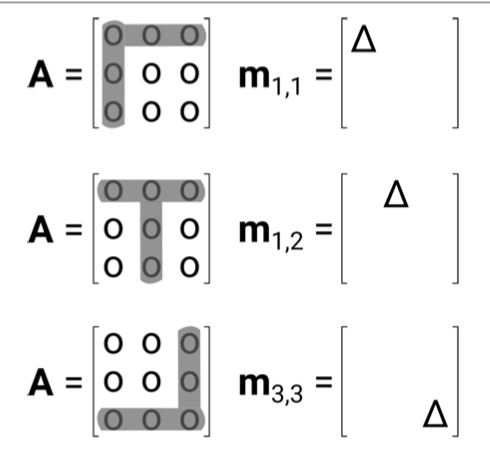
Thuật toán để tính nghịch đảo bao gồm bốn ma trận trung gian, gọi là ma trận minors, grid, cofactors, và adjugate:

---

Ma trận minors

Ma trận này bao gồm các định thức của các ma trận con. Mỗi phần tử $m_{i,j}$ của ma trận minors là định thức của ma trận con được tạo ra bằng cách loại bỏ hàng thứ $i$ và cột thứ $j$.

---