M03W2.3_Decision Tree

Important

Tham khảo

Table of Content

---

• Tham khảo
• I. Decision Tree là gì
  • Một số thuật ngữ
• II. Thuật toán phân tách trong Decision Tree: Entropy & Gini Impurity
  • II.1. Thuật ngữ và review công thức
  • II.2. Đề xuất ban đầu
  • II.3. Entropy & Information Gain
    • Entropy
    • Information Gain
  • II.4. Gini Impurity & Gini Gain
    • Gini Impurity
    • Gini Gain
  • II.5. So sánh Entropy/Information Gain và Gini/Gini Gain
• III. Xây dựng một Classification Tree (Step by Step)
  • Thực hành

    • Mô tả bài toán

    • Lời giải

I. Decision Tree là gì

Decision Tree là mô hình máy học mô phỏng quy trình ra quyết định. Ta có thể hình dung qua ví dụ: mỗi khi ra khỏi nhà, ta cân nhắc có nên mang theo ô không. Quyết định này bắt đầu từ câu hỏi “Trời có đang mưa?”. Nếu câu trả lời là đúng hoặc sai, ta sẽ đi theo một nhánh, rồi tiếp tục đặt câu hỏi khác cho đến khi có quyết định cuối cùng. Nếu Decision Tree được dùng để phân loại dữ liệu thành các nhóm rời rạc thì gọi là Classification Tree (Cây phân loại). Nếu dùng để dự đoán giá trị số liên tục thì gọi là Regression Tree (Cây hồi quy).

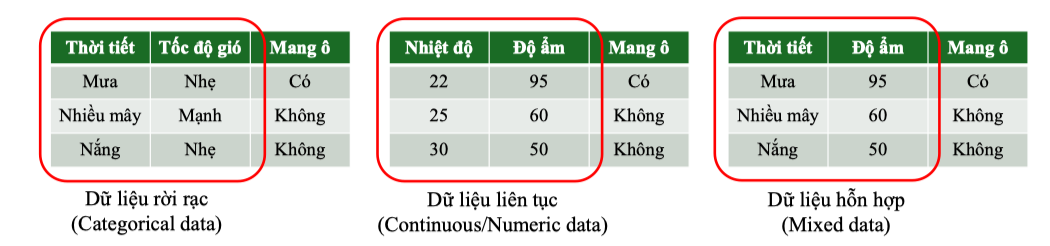
Decision Tree có thể xử lý đồng thời nhiều loại dữ liệu:

• Dữ liệu rời rạc (Categorical data):

  Ví dụ: “Mưa/Nắng/Nhiều mây”, “Có/Không”. Mỗi giá trị sẽ tạo một nhánh riêng.

• Dữ liệu liên tục (Continuous/Numeric data):

  Ví dụ: “Nhiệt độ”, “Độ ẩm”. Thuật toán sẽ tìm ngưỡng (threshold) tối ưu để phân chia dữ liệu.

• Dữ liệu hỗn hợp (Mixed data):

  Khi tập dữ liệu chứa cả biến rời rạc và biến liên tục, Decision Tree có thể kết hợp cả hai.

Một số thuật ngữ

Thuật ngữ	Định nghĩa
Root node (nút gốc)	Nút đầu tiên, vị trí khởi đầu, nằm ở đỉnh cao nhất của cây.
Internal node (nút phân nhánh)	Mỗi nút thực hiện một điều kiện kiểm tra, có các nhánh con.
Split (phân tách)	Thao tác chia tập dữ liệu tại một Internal node dựa trên giá trị hoặc ngưỡng của thuộc tính, tạo ra các nhánh con.
Branch (nhánh)	Đường kết nối giữa các nút, thể hiện kết quả True/False hoặc giá trị của biến rời rạc.
Leaf node (nút lá)	Nút cuối cùng, không còn nhánh con, đưa ra nhãn phân loại.
Depth (độ sâu)	Độ sâu của cây (chiều cao cây), là số nhánh dài nhất tính từ Root đến Leaf.
Pure (thuần/tinh khiết)	Nút mà tất cả các mẫu trong nó đều thuộc cùng một nhãn.
Impure (không thuần/không tinh khiết)	Nút có từ hai nhãn trở lên xuất hiện trong tập mẫu.
![[image 2 30.png	image 2 30.png]]

II. Thuật toán phân tách trong Decision Tree: Entropy & Gini Impurity

Trong quá trình xây dựng Decision Tree, bước quan trọng nhất là chọn thuộc tính để phân tách dữ liệu. Việc chọn thuộc tính ảnh hưởng trực tiếp đến độ chính xác và khả năng khái quát của mô hình. Hai tiêu chí thường được sử dụng là Entropy (thước đo mức độ hỗn độn) và Gini Impurity (thước đo mức độ không tinh khiết).

II.1. Thuật ngữ và review công thức

Ký hiệu	Ý nghĩa
$X,x_i$	Biến ngẫu nhiên $X$ và giá trị thứ $i$trong tập giá trị $\{x_i\}$.
$p_i=P(X=x_i)$	Xác suất để $X$ nhận giá trị $x_i$.
$\mu =\mathbb{E}[X]$	Kỳ vọng (mean) của $X$, ${\sum }_i{x}_i{p}_i$.
σ2=Var(X)\sigma^2 = Var(X)	Phương sai của XX, ∑i(xi−μ)2pi\sum_i (x_i - \mu)^2 p_i.
σ=σ2\sigma = \sqrt{\sigma^2}	Độ lệch chuẩn của XX.
SS	Tập dữ liệu ban đầu.
CC	Tập các nhãn (classes) trong SS.
pcp_c	Xác suất có nhãn cc trong SS.
I(E)I(E)	Lượng thông tin (information content) của biến cố EE (đơn vị: bit).
H(S)H(S)	Entropy của tập SS, đo độ hỗn độn của tập dữ liệu.
Vals(A)\text{Vals}(A)	Tập các giá trị (hoặc ngưỡng) của thuộc tính AA.
SvS_v	Tập con của SS gồm các mẫu có A=vA = v.
IG(S,A)IG(S, A)	Information Gain: Độ giảm trung bình của entropy khi phân tách tập SS theo thuộc tính AA.
G(S)G(S)	Gini Impurity: Mức độ không tinh khiết của tập SS theo chỉ số Gini.
GG(S,A)GG(S, A)	Gini Gain: Độ giảm impurity khi phân tách tập SS theo thuộc tính AA.
(	S
True/False	Nhãn rẽ nhánh cho kết quả kiểm tra điều kiện tại một node.

---

II.2. Đề xuất ban đầu

Giả sử ta có một túi gồm 9 viên bi đỏ và 1 viên bi xanh: Công thức xác suất: $P(\text{đỏ})=\frac{9}{10}=0.9,P(\text{xanh})=\frac{1}{10}=0.1$ Rõ ràng, việc rút được viên bi xanh gây “ngạc nhiên” nhiều hơn viên bi đỏ. Ta mong muốn có một cách đo lường chính xác mức độ “ngạc nhiên” này. Một cách tiếp cận ban đầu là định nghĩa: $Surprise(E)=\frac{1}{P(E)}$ Hàm này thoả mãn tính chất: sự kiện càng hiếm (P(E) ↓) thì Surprise(E) ↑. Tuy nhiên, tồn tại một số vấn đề:

1. Đơn vị mơ hồ: ví dụ, nếu $P(E)=0.1\Rightarrow Surprise(E)=10$. Vậy “10” này là gì? Không thể gọi là “10 ngạc nhiên”.

2. Không cộng dồn: với hai biến cố độc lập $E_1,E_2$, ta mong muốn:

   $Surprise(E_1\cap E_2)=Surprise(E_1)+Surprise(E_2)$

   Nhưng thực tế:

   $Surprise(E_1\cap E_2)=\frac{1}{P(E_1)P(E_2)}=Surprise(E_1)\times Surprise(E_2)$

   Do đó, cần một định nghĩa khác để thỏa mãn tính chất cộng dồn.

—- Theo Shannon, hàm thông tin $I(p)$ phải thỏa mãn ba điều kiện:

1. Tính liên tục: $I(p)$ liên tục theo $p$.

2. Đơn điệu: $I(p)$ giảm khi $p$ tăng

3. Tính cộng dồn: Với hai biến cố độc lập:

   $I(p_1{p}_2)=I(p_1)+I(p_2)$

Từ đây ta có hàm duy nhất (ngoại trừ hằng số tỉ lệ) thoả mãn các điều kiện trên là: $I(E)=-{\log }_{2}P(E)\text{(đơn vị: bit)}$ Ví dụ với hai biến cố độc lập $E_1,E_2$: $I(E_1\cap E_2)=-{\log }_2(P(E_1)P(E_2))=I(E_1)+I(E_2)$ Như vậy, Shannon chứng minh rằng chỉ có hàm logarit mới thỏa mãn các điều kiện lý thuyết thông tin. Cơ số log có thể là bất kỳ, nhưng thường dùng log base 2 để đo thông tin bằng bit.

II.3. Entropy & Information Gain

Entropy

Từ hàm thông tin $I(E)$, Entropy $H$ của một tập dữ liệu $S$ với phân phối xác suất $\{p_c{\}}_{c\in C}$ được định nghĩa: $H(S)=-{\sum }_{c\in C}{p}_c{\log }_2{p}_c\text{(đơn vị: bit)}$ Trong đó:

• $S$: tập dữ liệu ban đầu.
• $C$: tập các nhãn (classes).
• $p_c$: xác suất để một phần tử trong $S$ có nhãn $c$. Ý nghĩa:
• Entropy càng lớn → dữ liệu càng “không thuần” (Impure), tức là càng khó phân loại.
• Entropy càng nhỏ → dữ liệu càng “thuần” (Pure), dễ phân tách. Lưu ý:
• $H(S)=0$: khi tập dữ liệu $S$ chỉ có một lớp duy nhất, hoàn toàn thuần (Pure)
• $H(S)=1$: đạt cực đại khi $S$ có 2 nhãn phân phối đều nhau (bài toán phân loại nhị phân).
• Với $C>2$: nếu dữ liệu phân phối đều trên nhiều nhãn, thì: $H(S)={\log }_2|C|$ Điều này cho thấy Entropy phụ thuộc không chỉ vào số lượng nhãn, mà còn vào mức độ phân bố của chúng.

Ví dụ: 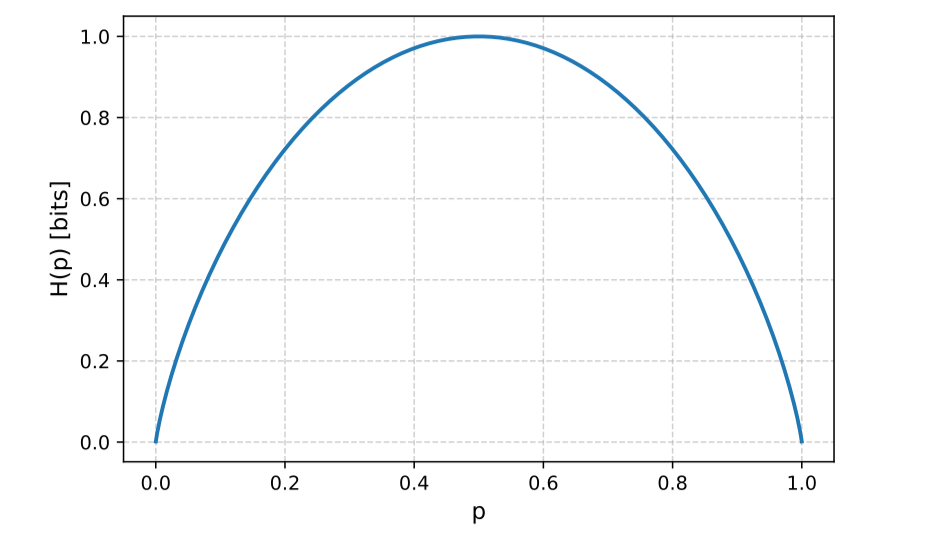Hàm Entropy trong bài toán phân loại nhị phân được viết: $H(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p),p\in (0,1)$ Nhận xét từ đồ thị:

• Khi $p\to 0$ hoặc $p\to 1$: $H(p)\to 0$

  → Tập dữ liệu gần như chắc chắn thuộc về một nhãn duy nhất → hoàn toàn thuần khiết (Pure).

• Khi $p=0.5$: $H(p)$ đạt cực đại bằng 1 bit.

  → Tập dữ liệu phân bố đều giữa 2 nhãn (ví dụ: “Đúng/Sai”, “Có/Không”) → mức độ hỗn độn cao nhất.

• Với số nhãn lớn hơn ($|C|>2$): giá trị cực đại của Entropy sẽ cao hơn, cụ thể đạt ${\log }_2|C|$ khi dữ liệu được phân bố đều trên tất cả các nhãn. Diễn giải trực quan:

• Nhãn càng lệch hẳn về một phía → Entropy thấp.

• Nhãn càng cân bằng → Entropy cao.

---

Information Gain

Khi phân tách tập dữ liệu $S$ theo một thuộc tính $A$, ta tính Information Gain (IG) để đo mức độ giảm “hỗn độn” sau phân tách: $IG(S,A)=H(S)-{\sum }_{v\in Vals(A)}\frac{|S_v|}{|S|}H(S_v)$ Trong đó:

• $A$: thuộc tính dùng để phân tách
• $Vals(A)$: tập các giá trị (hoặc ngưỡng) có thể có của $A$.
• $S_v$: tập con của $S$ gồm các mẫu có $A=v$.
• $|S_v|/|S|$: là trọng số theo kích thước tập con. Ý nghĩa:
• $IG(S,A)$ càng lớn → thuộc tính $A$ giúp dữ liệu trở nên “thuần” hơn sau phân tách.
• Khi xây dựng cây quyết định, ta chọn thuộc tính có IG lớn nhất để làm nút phân tách.

Information Gain khuyến khích chọn thuộc tính có nhiều nhánh, nhưng điều này có thể dẫn đến overfitting. Để khắc phục, một số thuật toán sử dụng Gain Ratio

---

II.4. Gini Impurity & Gini Gain

Ngoài Entropy, một tiêu chí phổ biến khác để đo mức độ hỗn độn trong Decision Tree là Gini Impurity. Chỉ số này được đề xuất bởi Breiman et al. (1984) và được sử dụng trong thuật toán CART (Classification and Regression Tree).

Gini Impurity

Gini Impurity của tập dữ liệu $S$ được định nghĩa: $G(S)={\sum }_{c\in C}{p}_c(1-p_c)=1-{\sum }_{c\in C}{p}_c^2$ Trong đó:

• $C$: tập các nhãn (classes).
• $p_c$: xác suất xuất hiện của nhãn $c$ trong $S$.
• $G(S)$: mức “không tinh khiết” (impurity) trong phân phối nhãn.

---

Gini Gain

Khi phân tách tập $S$ theo thuộc tính $A$ thành các tập con $\{S_v\},v\in Vals(A)$, Gini Gain được tính: $GG(S,A)=G(S)-{\sum }_{v\in Vals(A)}\frac{|S_v|}{|S|}G(S_v)$ Trong đó:

• $S_v$: tập con gồm các mẫu có $A=v$.
• $\frac{|S_v|}{|S|}$: trọng số theo kích thước tập con.
• $GG(S,A)$: mức giảm impurity nhờ phân tách theo $A$. Lưu ý quan trọng
• $G(S)=0$ khi dữ liệu hoàn toàn thuần (Pure), tức chỉ có một nhãn duy nhất.
• $G(S)=0.5$ khi dữ liệu có 2 nhãn phân bố đều (trường hợp phân loại nhị phân).
• Với nhiều hơn 2 nhãn ($|C|>2$): nếu dữ liệu phân bố đều, ta có: $G(S)=1-\frac{1}{|C|}$ So với Entropy, Gini Impurity thường được ưu tiên trong thực tế vì tính toán nhanh hơn (không có logarit). Cả hai tiêu chí đều cho kết quả tương tự nhau, nhưng Gini thường phù hợp hơn khi cần tốc độ.

---

II.5. So sánh Entropy/Information Gain và Gini/Gini Gain

Giống nhau	Khác nhau
Cả hai đều đánh giá chất lượng phân tách dựa trên mức độ “thuần” (Pure) của nhãn.	Entropy/Information Gain sử dụng log để đo “độ ngạc nhiên” trung bình; trong khi Gini/Gini Gain không dùng log → tính nhanh hơn.
Cả hai đều sử dụng trọng số $\frac{\Vert S_v\Vert }{\Vert S\Vert }$khi kết hợp giá trị trên nhánh con.	Entropy nhạy hơn với các nhãn có tần suất nhỏ (hiếm); Gini Impurity ưu tiên tạo các node thuần và ít dao động theo tần suất.

---

III. Xây dựng một Classification Tree (Step by Step)

Để xây dựng một cây quyết định, ta thực hiện quy trình 4 bước chính như sau: Bước 1: Tính thống kê gốc (Root Entropy hoặc Gini)

• Tính Entropy $H(S)$ cho toàn bộ tập dữ liệu (dựa trên cột nhãn).
• Nếu dùng Gini: tính Gini Impurity $G(S)$ cho toàn bộ tập. Bước 2: Tính Gain cho từng thuộc tính
• Với Entropy: $IG(S,A)=H(S)-{\sum }_{v\in Vals(A)}\frac{|S_v|}{|S|}H(S_v)$
• Với Gini: $GG(S,A)=G(S)-{\sum }_{v\in Vals(A)}\frac{|S_v|}{|S|}G(S_v)$

Bước 3: Chọn thuộc tính để phân nhánh

• Chọn thuộc tính có Information Gain hoặc Gini Gain cao nhất.
• Phân tách dữ liệu theo giá trị của thuộc tính đó.
• Lặp lại Bước 1 → 3 cho từng node con, cho đến khi:
  • Node đạt mức tinh khiết (pure) (tức tất cả các mẫu có cùng nhãn), hoặc
  • Không còn thuộc tính nào để phân chia. Bước 4: Ứng dụng cây để dự đoán
• Với một mẫu mới, bắt đầu từ root node, kiểm tra điều kiện → đi theo nhánh tương ứng → đến leaf node → trả về nhãn tương ứng.

Việc dừng cây tại đúng thời điểm (khi đủ tinh khiết hoặc không còn thuộc tính) giúp tránh overfitting. Một số thuật toán còn sử dụng kỹ thuật pruning (cắt tỉa cây) để tối ưu thêm.

Thực hành

Mô tả bài toán

Bộ dữ liệu:

STT	Điểm Tốt Nghiệp	Chứng chỉ IELTS	Cộng Điểm Dân Tộc	Đậu Đại Học
1	12.0	Không	Không	Không
2	14.5	Không	Có	Không
3	16.0	Không	Không	Không
4	18.0	Không	Có	Không
5	20.0	Có	Không	Có
6	22.0	Không	Không	Không
7	24.0	Có	Có	Có
8	26.0	Không	Không	Có
Phân tích thuộc tính:

• Điểm Tốt Nghiệp: Biến liên tục (numeric) → cần tìm ngưỡng phân tách tối ưu.
• Chứng chỉ IELTS: Biến rời rạc (categorical) → giá trị “Có” / “Không”.
• Cộng Điểm Dân Tộc: Biến rời rạc (categorical) → giá trị “Có” / “Không”.
• Đậu Đại Học: Nhãn đầu ra (label) → “Có” hoặc “Không”.

Mục tiêu bài toán: Xây dựng Classification Tree dựa trên hai tiêu chí:

1. Entropy & Information Gain → Tính entropy ban đầu và thông tin thu được khi tách theo từng thuộc tính.
2. Gini Impurity & Gini Gain → Tính impurity ban đầu và mức giảm impurity khi tách theo từng thuộc tính. Dự đoán kết quả cho học sinh mới có thông tin như sau:

• Điểm Tốt Nghiệp = 21.0
• Chứng chỉ IELTS = Không
• Cộng Điểm Dân Tộc = Có Hãy sử dụng cây quyết định bạn vừa xây dựng để dự đoán xem thí sinh có đậu đại học hay không.

Khi xử lý thuộc tính liên tục như “Điểm Tốt Nghiệp”, nên thử các ngưỡng phân chia giữa từng cặp điểm liên tiếp (ví dụ: ngưỡng giữa 18.0 và 20.0 là 19.0), và tính Entropy hoặc Gini tại từng ngưỡng để chọn ra ngưỡng tốt nhất.

---

Lời giải

Bước 1: Tính thống kê gốc Tập dữ liệu ban đầu $S_0$ gồm 8 học sinh, với nhãn:

• “CÓ” = 3
• “KHÔNG” = 5 Tính xác suất: $p_{\text{Coˊ}}=\frac{3}{8},p_{\text{Khoˆng}}=\frac{5}{8}$ Tính Entropy của gốc: $H(S_0)=-\frac{3}{8}{\log }_2\frac{3}{8}-\frac{5}{8}{\log }_2\frac{5}{8}\approx 0.9544$ Tính Gini của gốc: $G(S_0)=1-\left({\left(\frac{3}{8}\right)}^2+{\left(\frac{5}{8}\right)}^2\right)\approx 0.4688$ Bước 2: Tính Gain “Điểm Tốt Nghiệp” (numeric): cách xử lý dữ liệu liên tục:

1. Sắp xếp điểm tốt nghiệp tăng dần.
2. Tạo 7 ngưỡng (do có 8 mẫu) phân chia từ giá trị trung bình của các cặp liên tiếp: $\text{Caˊc ngưỡng}=\frac{12+14.5}{2},\frac{14.5+16}{2},\dots ,\frac{24+26}{2}$ → Các ngưỡng: 13.25, 15.25, 17.0, 19.0, 21.0, 23.0, 25.0 Ví dụ với ngưỡng 13.25:

• Xét điều kiện: Điểm < 13.25

  → Duy nhất 1 học sinh: điểm = 12, nhãn = “Không”

• Nhánh trái: 1 mẫu → Pure

• Nhánh phải: gồm 7 học sinh còn lại

  → Có 3 “CÓ”, 4 “KHÔNG” → Impure

  $H(\text{False})=-\frac{3}{7}{\log }_2\frac{3}{7}-\frac{4}{7}{\log }_2\frac{4}{7}\approx 0.9852$

  $G(\text{False})=1-\left({\left(\frac{3}{7}\right)}^2+{\left(\frac{4}{7}\right)}^2\right)\approx 0.4898$

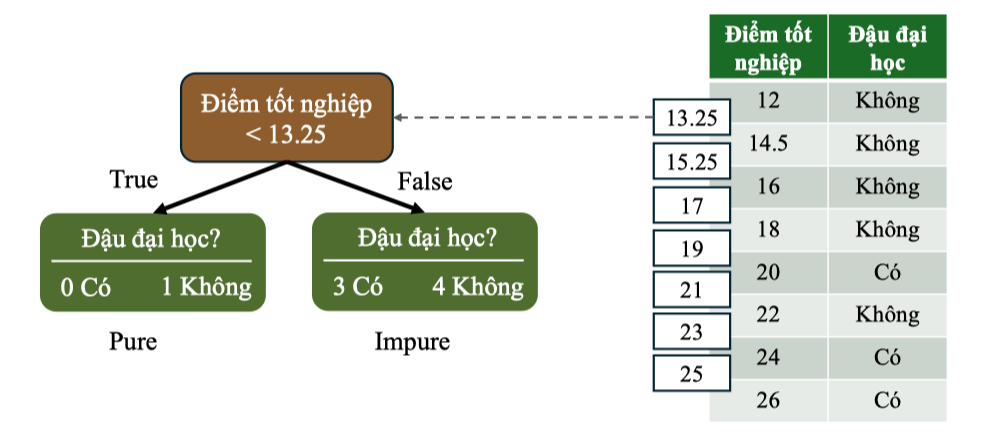Tính Gain:

• Information Gain: $IG=0.9544-\left(\frac{1}{8}\cdot 0+\frac{7}{8}\cdot 0.9852\right)\approx 0.0924$

• Gini Gain: $GG=0.4688-\left(\frac{1}{8}\cdot 0+\frac{7}{8}\cdot 0.4898\right)\approx 0.0402$ Tương tự, tính lần lượt cho từng ngưỡng và ta có: |Ngưỡng Điểm|Information Gain|Gini Gain| |---|---|---| |13.25|0.0924|0.0402| |15.25|0.2044|0.0938| |17.00|0.3476|0.1688| |19.00|0.5488|0.2812| |21.00|0.1589|0.1021| |23.00|0.4669|0.2605| |25.00|0.1992|0.1116| → Kết luận:

• Ngưỡng 19.00 cho IG và GG cao nhất

• Tách theo ngưỡng này giúp tăng độ “thuần” mạnh nhất cho các node con

  → Đây sẽ là lựa chọn phân tách đầu tiên nếu ta xây cây theo “Điểm Tốt Nghiệp”.

Việc chọn ngưỡng đúng không chỉ giúp tăng độ chính xác mà còn làm cây quyết định gọn và dễ hiểu hơn.

---

Chứng chỉ IELTS 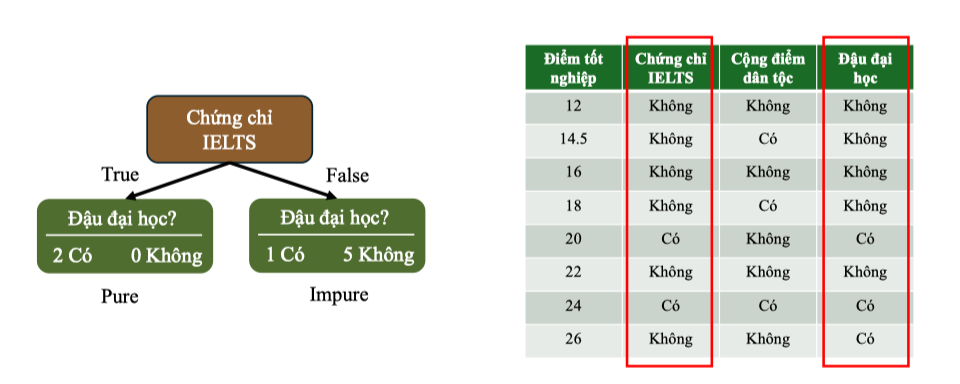→ Nhánh True (Có) là node thuần: toàn bộ đều “Đậu Đại Học” → Nhánh False (Không) là node không thuần, gồm cả “Có” và “Không”

Tính Entropy

• Nhánh True: $H(\text{True})=0$
• Nhánh False: $H(\text{False})=-\frac{1}{6}{\log }_2\frac{1}{6}-\frac{5}{6}{\log }_2\frac{5}{6}\approx 0.650$ Tính Information Gain $$\begin{gathered} IG(S_0,\text{Chứng chỉ IELTS})=H(S_0)-\left(\frac{2}{8}\cdot 0+\frac{6}{8}\cdot 0.650\right) \\ =0.9544-0.4875=0.4669 \end{gathered}$$

---

Tính Gini Impurity

• Nhánh True: $G(\text{True})=0$
• Nhánh False: $G(\text{False})=1-\left({\left(\frac{1}{6}\right)}^2+{\left(\frac{5}{6}\right)}^2\right)\approx 0.2778$ Tính Gini Gain

undefined