An Hoai Thai's Notes

M04W1.4_Random Forest Advanced Concepts and Its Applications

đọc 27 phút

Table of Content

Important

Tham khảo

M03W2.3_Decision Tree

M04W1.3_Warmup Random Forest ví dụ tính tay

1. Decision Tree Review

1.1. Giới thiệu bài toán

Bối cảnh: khi một vaccine ra đời, ta muốn dự đoán mức hiệu quả (%) tương ứng với liều lượng (unit) dùng cho bệnh nhân. Ví dụ dưới đây minh họa cách dùng Cây quyết định để suy đoán hiệu quả của liều bất kỳ dựa trên dữ liệu quan sát. Bảng dữ liệu quan sát (mỗi hàng là một ca thử nghiệm) cho biết liều vaccine (unit) và hiệu quả (effect, %). Nhiệm vụ: học một hàm quyết định từ dữ liệu để dự đoán hiệu quả khi tiêm 5 đơn vị.

Unit (đơn vị)Effect (hiệu quả) (%)
1098
200
35100
544
……
![[image 77.pngimage 77.png]]
Cây quyết định thực hiện việc chia nhỏ không gian dữ liệu dựa trên các ngưỡng (thresholds) để tìm ra vùng có dự đoán hiệu quả ổn định.
Trên đồ thị, trục ngang biểu diễn Unit (đơn vị vaccine), trục dọc biểu diễn Effectiveness (%).
  • Vùng Unit < 14.5: các điểm dữ liệu có hiệu quả gần 0%, cây dự đoán giá trị trung bình ≈ 4.2%.
  • Vùng 14.5 ≤ Unit < 23.5: hiệu quả cao (dữ liệu tập trung ở mức 100%), cây dự đoán ≈ 100%.
  • Vùng 23.5 ≤ Unit < 29: hiệu quả dao động, cây dự đoán trung bình ≈ 52.8%.
  • Vùng Unit ≥ 29: hiệu quả gần 0%, cây dự đoán ≈ 2.5%.

Sai số dự đoán trong Decision Tree Regression

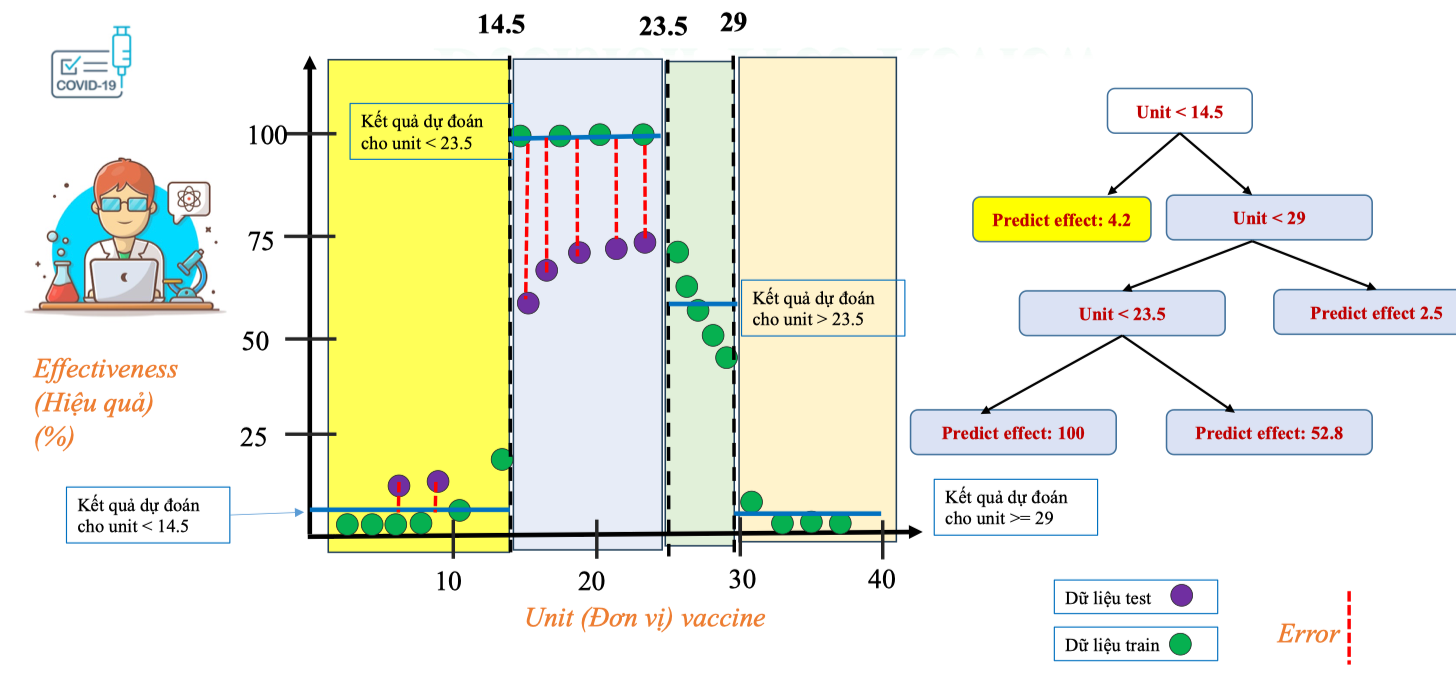
Trong mô hình Decision Tree Regression, ngoài việc học quy tắc chia ngưỡng để dự đoán, ta còn quan tâm đến mức độ sai lệch (Error) giữa giá trị thật và giá trị dự đoán. image 1 38.png

  • Dữ liệu train (màu xanh lá): được dùng để xây dựng cây, xác định các ngưỡng 14.5, 23.5 và 29.
  • Dữ liệu test (màu tím): không dùng trong quá trình học, mà để kiểm tra mức độ tổng quát (generalization) của mô hình. Trên đồ thị, các điểm test (màu tím) nằm trong vùng 14.5 ≤ Unit < 23.5 cho thấy có sự chênh lệch đáng kể so với đường dự đoán (100%). Sai số này được thể hiện bằng đường gạch đỏ (Error).

Pruning Tree (tỉa cây)

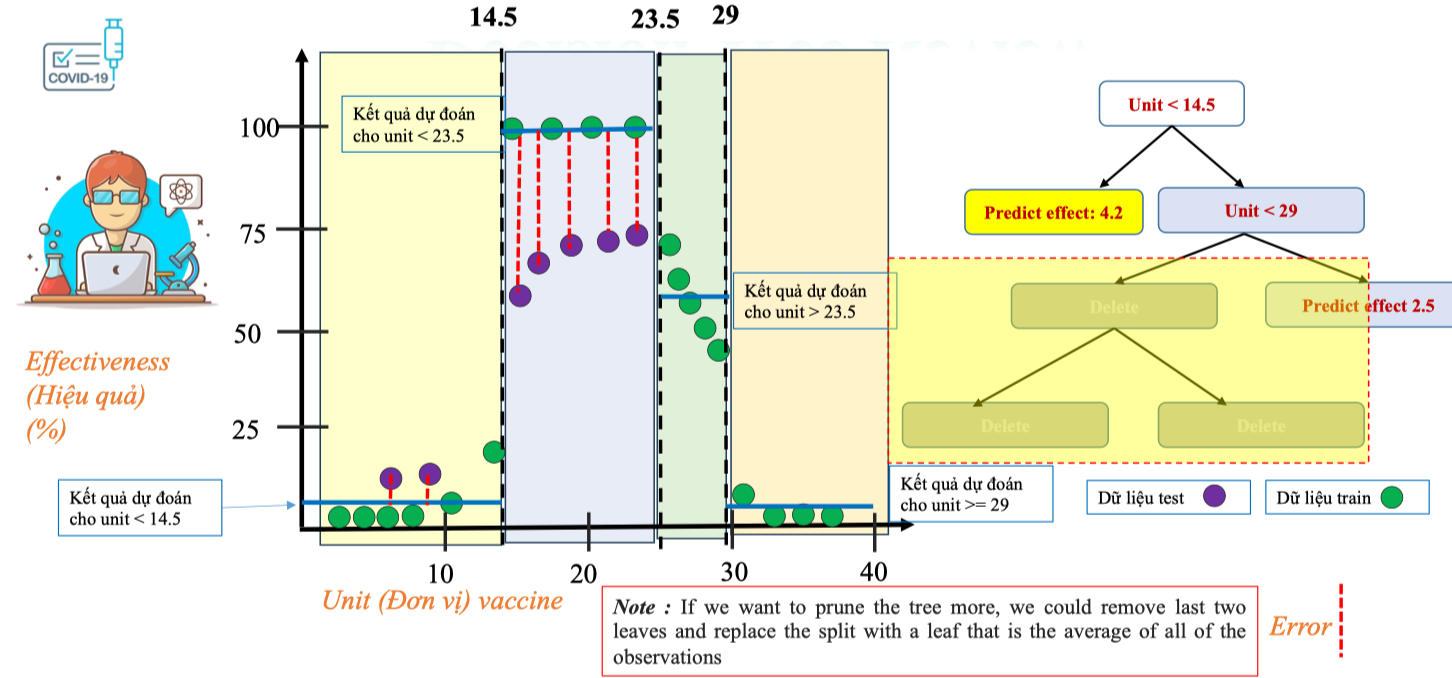
Ở trên Decision Tree của chúng ta đã bị overfitting – mô hình khớp rất tốt với dữ liệu train nhưng sai số lớn trên dữ liệu test. Để cải thiện, ta có thể dùng kỹ thuật pruning (cắt tỉa cây). image 2 36.png

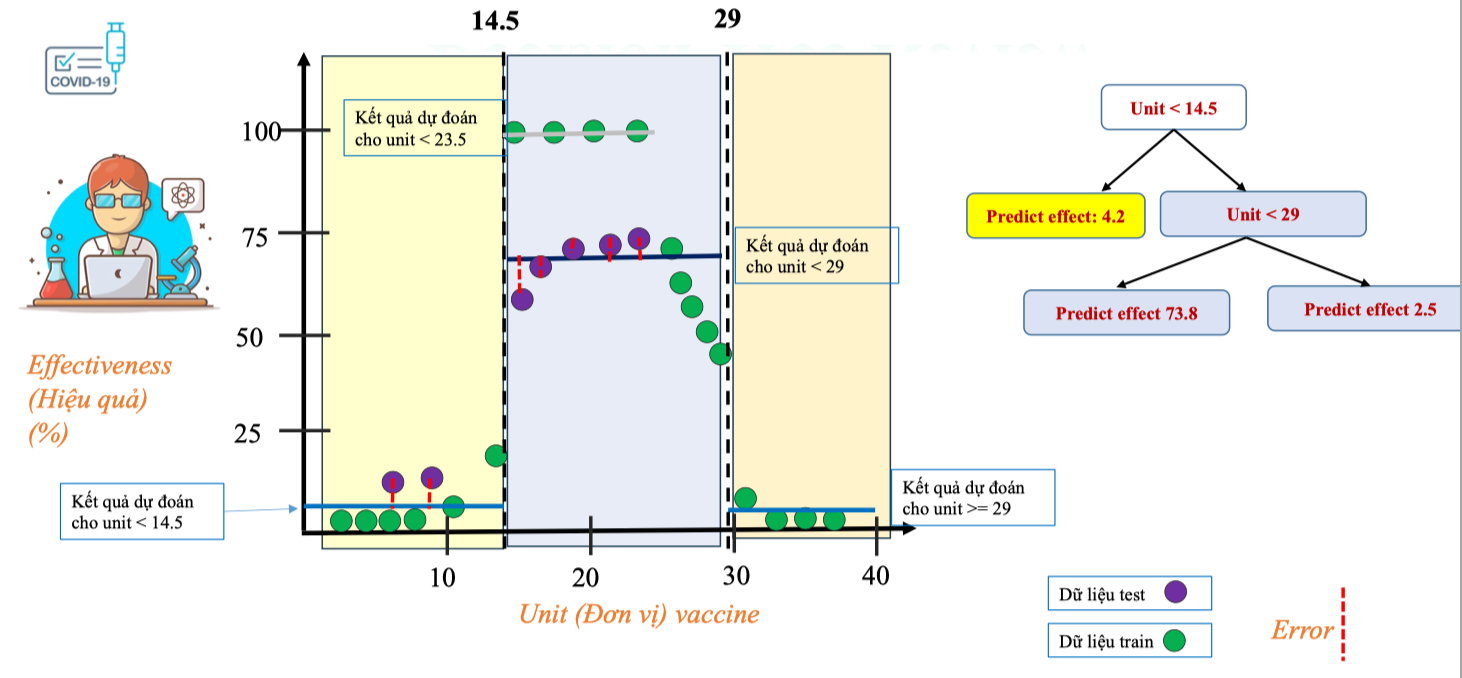
Kết quả image 3 34.png

1.2. Tree Complexity Penalty

How to select alpha

image 4 29.png

1.3. Advantages and Disadvantages

Advantages (Ưu điểm)

  • Rất dễ giải thích

    Decision Tree có cấu trúc trực quan, gần gũi như một chuỗi các câu hỏi “có/không”. Vì vậy, nhiều người không chuyên cũng có thể hiểu được cách mô hình đưa ra dự đoán.

  • Phản ánh gần giống cách suy nghĩ của con người

    Khi ra quyết định, con người cũng thường phân nhánh theo các điều kiện cụ thể. Điều này làm cho Decision Tree dễ được chấp nhận trong các lĩnh vực cần tính minh bạch.

  • Xử lý dễ dàng các biến định tính (qualitative predictors)

    Không cần tạo thêm dummy variables (biến giả) như trong hồi quy tuyến tính. Ví dụ, biến Màu sắc = {Đỏ, Xanh, Vàng} có thể chia trực tiếp thành các nhánh mà không cần mã hóa thành 0/1.

Disadvantages (Nhược điểm)

  1. Độ chính xác dự đoán thấp hơn

    So với nhiều phương pháp regression hoặc classification hiện đại (như Random Forest, Gradient Boosting, SVM), cây đơn thường kém chính xác hơn.

  2. Nhạy cảm với thay đổi dữ liệu

    Chỉ một thay đổi nhỏ trong dữ liệu có thể dẫn đến cấu trúc cây rất khác nhau → mô hình thiếu ổn định.

  3. Kém hiệu quả trong bài toán regression liên tục

    Khi mục tiêu là dự đoán biến liên tục (ví dụ: giá nhà, nhiệt độ), Decision Tree thường cho kết quả kém mượt, dạng bậc thang chứ không trơn tru.

Dummy Variable

Dummy Variable (biến giả) là cách mã hóa các biến định tính (categorical variables) thành biến nhị phân (0/1) để có thể sử dụng trong các mô hình hồi quy tuyến tính hoặc các thuật toán cần dữ liệu số. Ví dụ:

  • Biến Temperature có 3 giá trị: Hot, Warm, Cold.
  • Sau khi chuyển thành dummy variables:
    • var_hot = 1 nếu Hot, 0 nếu không
    • var_warm = 1 nếu Warm, 0 nếu không
    • var_cold = 1 nếu Cold, 0 nếu không Bảng minh họa
WaterTemperaturevar_hotvar_warmvar_cold
AHot100
BCold001
CWarm010
DCold001

Điểm mạnh của Decision Tree là không cần tạo dummy variables. Ví dụ: biến Gender có thể được chia trực tiếp thành 2 nhánh (Male / Female) thay vì phải chuyển sang 0/1. Điều này giúp mô hình:

  • Giữ nguyên tính dễ hiểu.
  • Tránh làm dữ liệu phình to khi có nhiều biến định tính. 💡 Tip: Với các thuật toán hồi quy tuyến tính hay logistic regression, dummy variables là bắt buộc. Nhưng với Decision Tree hoặc Random Forest, việc này không cần thiết vì mô hình tự xử lý nhánh theo giá trị của biến phân loại.

Bias-Variance Trade-off

Khái niệm:

  • Bias (độ chệch): sai số do mô hình quá đơn giản, không thể nắm bắt mối quan hệ thật trong dữ liệu. → dẫn đến underfitting.
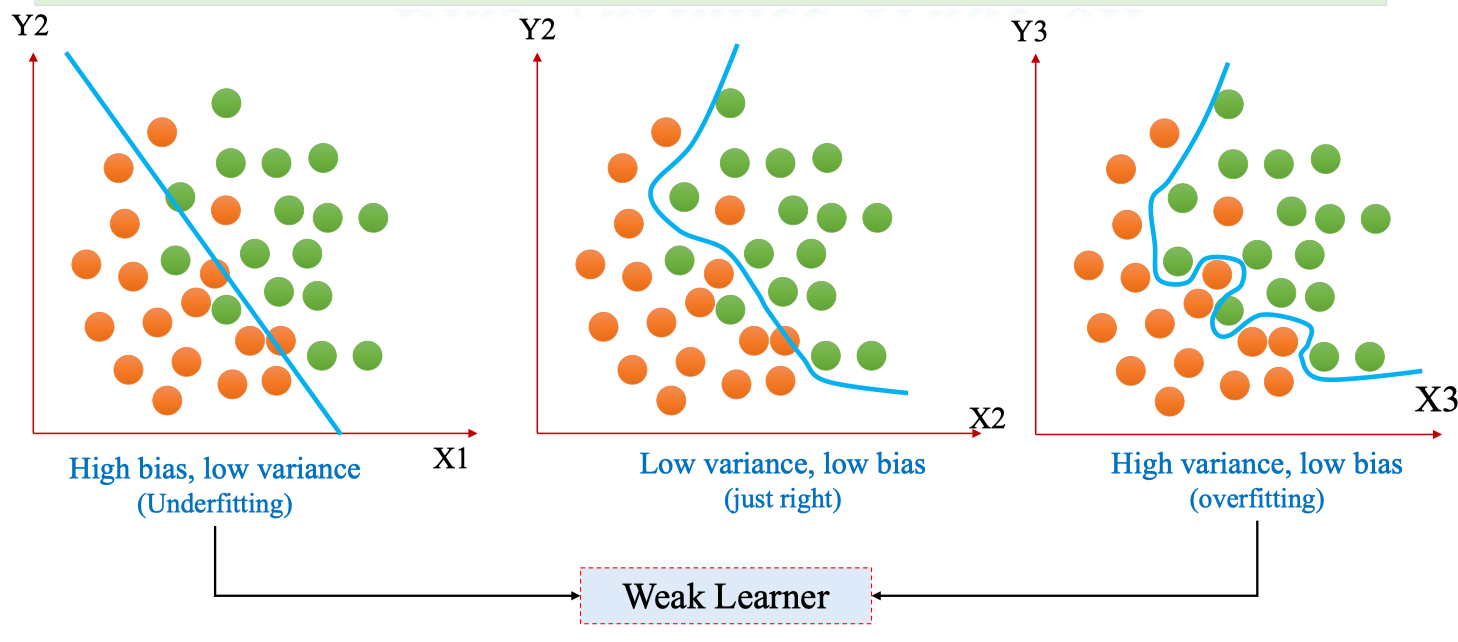
  • Variance (phương sai): mức độ thay đổi của mô hình khi dữ liệu huấn luyện thay đổi. → variance cao nghĩa là mô hình quá nhạy với dữ liệu → overfitting. image 5 27.png
  • High bias, low variance (Underfitting)
    • Mô hình quá đơn giản (ví dụ: đường thẳng phân loại).
    • Không thể nắm bắt ranh giới phức tạp giữa 2 lớp.
    • Kết quả: dự đoán kém trên cả train lẫn test.
  • Low bias, low variance (Just right)
    • Mô hình đủ linh hoạt để bắt được cấu trúc dữ liệu.
    • Có khả năng tổng quát tốt.
    • Đây là trạng thái lý tưởng.
  • High variance, low bias (Overfitting)
    • Mô hình quá phức tạp, nắm bắt cả nhiễu (noise) trong dữ liệu train.
    • Dự đoán rất tốt trên train nhưng sai số lớn trên test. Weak Learner và liên hệ với Decision Tree
  • Một Decision Tree đơn thường được coi là weak learner vì dễ rơi vào bias cao (cây nông) hoặc variance cao (cây sâu).
  • Các kỹ thuật ensemble như Bagging (Random Forest) hay Boosting được dùng để kết hợp nhiều weak learners → thành strong learner, cải thiện cân bằng giữa bias và variance. Quan hệ thật trong dữ liệu
  • Trên thực tế, dữ liệu có một mối quan hệ tiềm ẩn (true relationship) giữa các biến đầu vào (Weight) và đầu ra (Height).
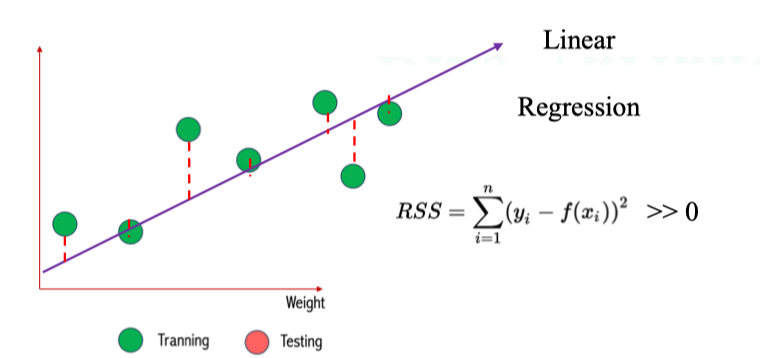
  • Ví dụ: chiều cao thường tăng theo cân nặng, nhưng sau một mức nào đó sẽ ổn định. 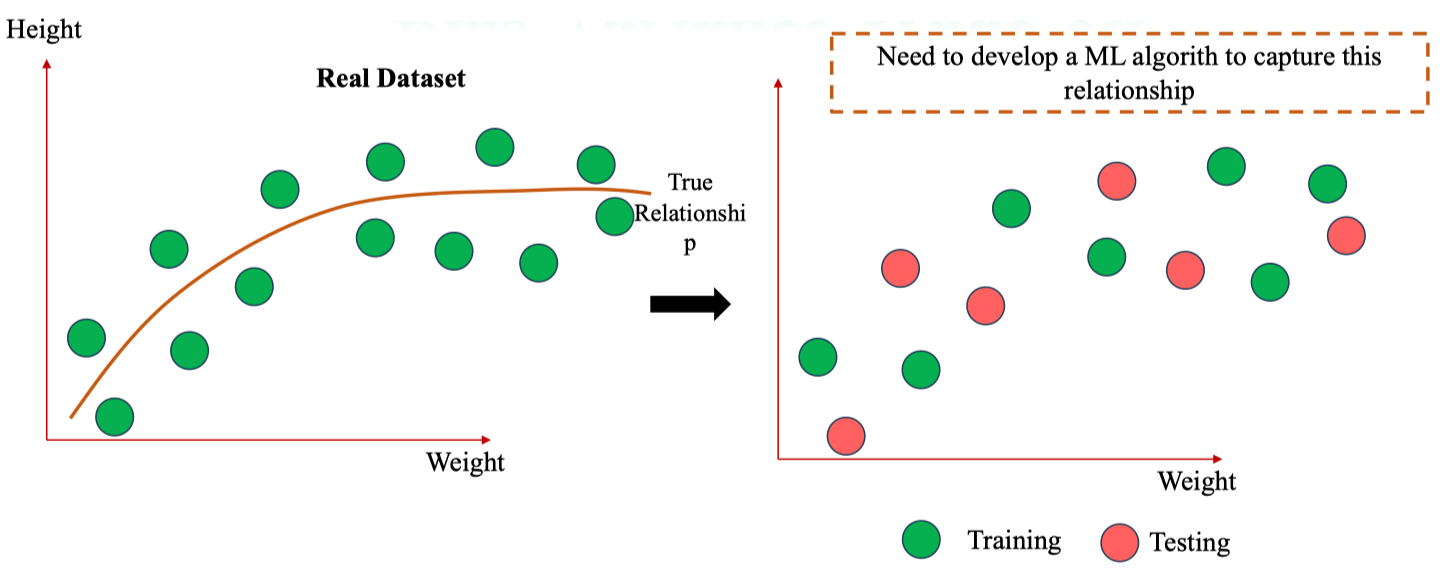image 6 25.png Linear Regression → High Bias
  • Với mối quan hệ thật giữa Weight (cân nặng) và Height (chiều cao) có dạng cong, Linear Regression (hồi quy tuyến tính) chỉ fit được một đường thẳng.
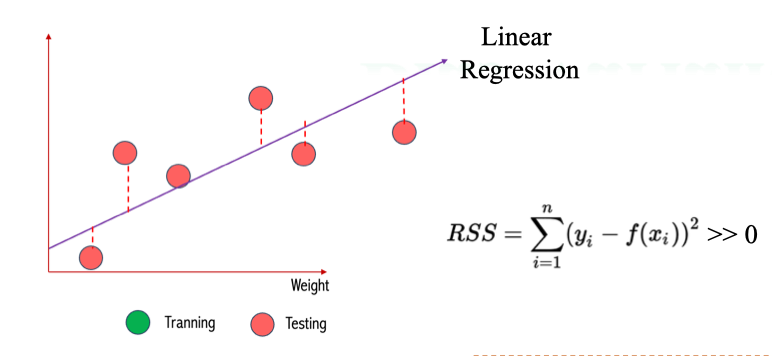
  • Kết quả: không thể bắt được quan hệ thật → bias cao (underfitting). image 7 20.png image 8 20.png

Polynomial Regression → Low Bias

  • Polynomial Regression (hồi quy đa thức) có thể uốn cong để khớp gần như hoàn toàn dữ liệu huấn luyện.
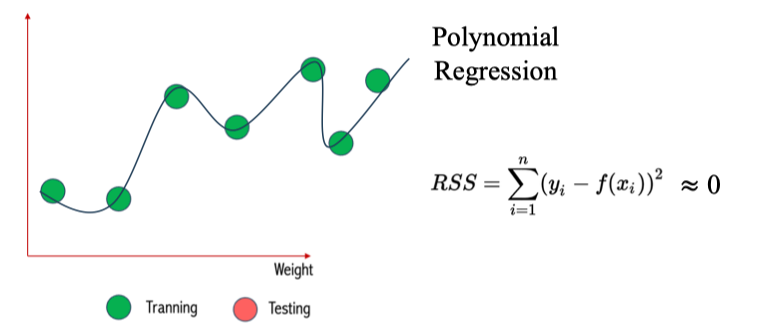
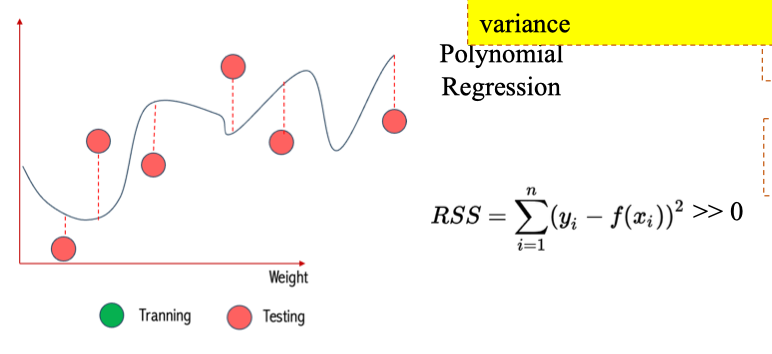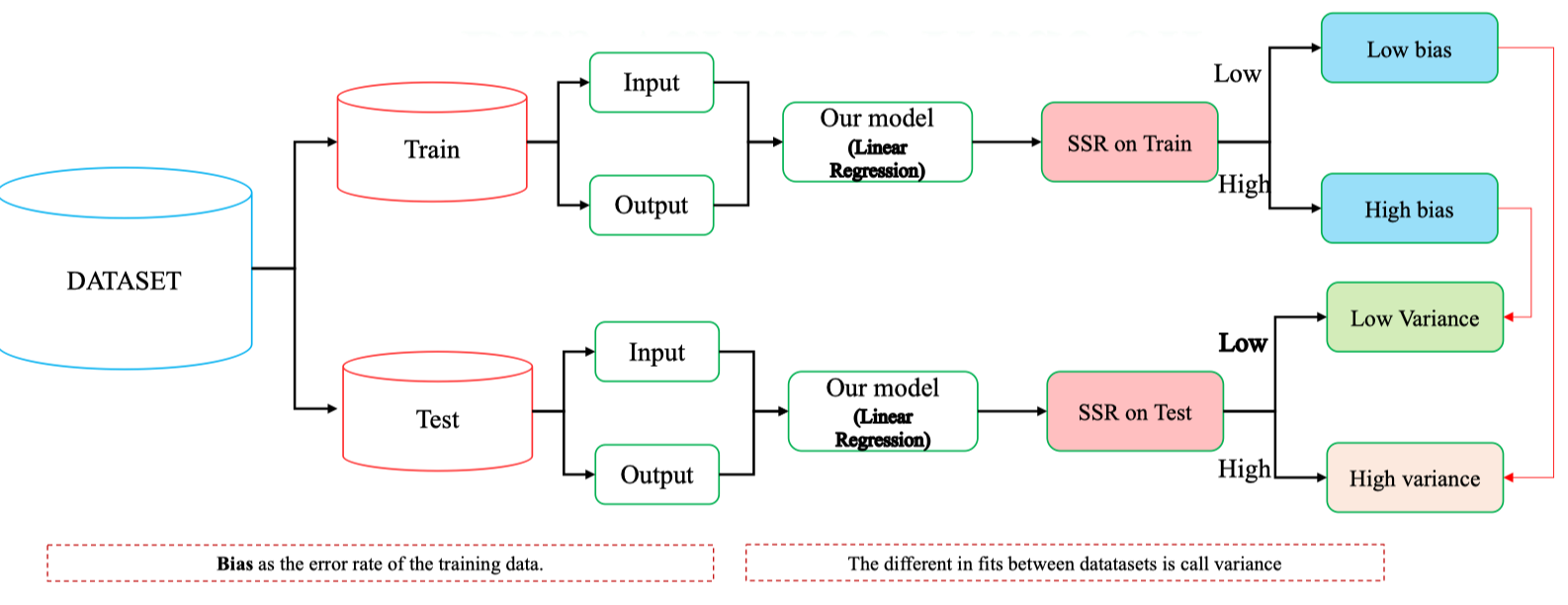
  • Kết quả: bias thấp (khớp tốt mối quan hệ thật). image 9 19.png image 10 18.png Tổng kết: đánh giá Bias-Variance image 11 18.png
  • Dataset được chia thành hai phần:
    • Train set: dùng để huấn luyện mô hình (ví dụ Linear Regression).
    • Test set: dùng để đánh giá khả năng tổng quát hóa của mô hình.
  • Với mỗi tập, ta đưa Input vào mô hình, so sánh Output dự đoán với giá trị thật → tính toán SSR (Sum of Squared Residuals). Đánh giá:
  • Bias (độ chệch): sai số trên tập huấn luyện (train).
    • Nếu SSR trên train cao → High bias (mô hình underfitting).
    • Nếu SSR trên train thấp → Low bias (mô hình học được quan hệ tốt).
  • Variance (phương sai): sự khác biệt giữa train error và test error.
    • Nếu SSR trên test gần với train → Low variance (mô hình ổn định).
    • Nếu SSR trên test khác biệt lớn với train → High variance (mô hình overfitting). image 12 17.png
  • Mục tiêu của học máy không phải là train error thấp nhất, mà là đạt test error tối ưu.
  • Bias–variance trade-off chính là nền tảng để lựa chọn mô hình phù hợp.

2. Random Forest

2.1 Motivation

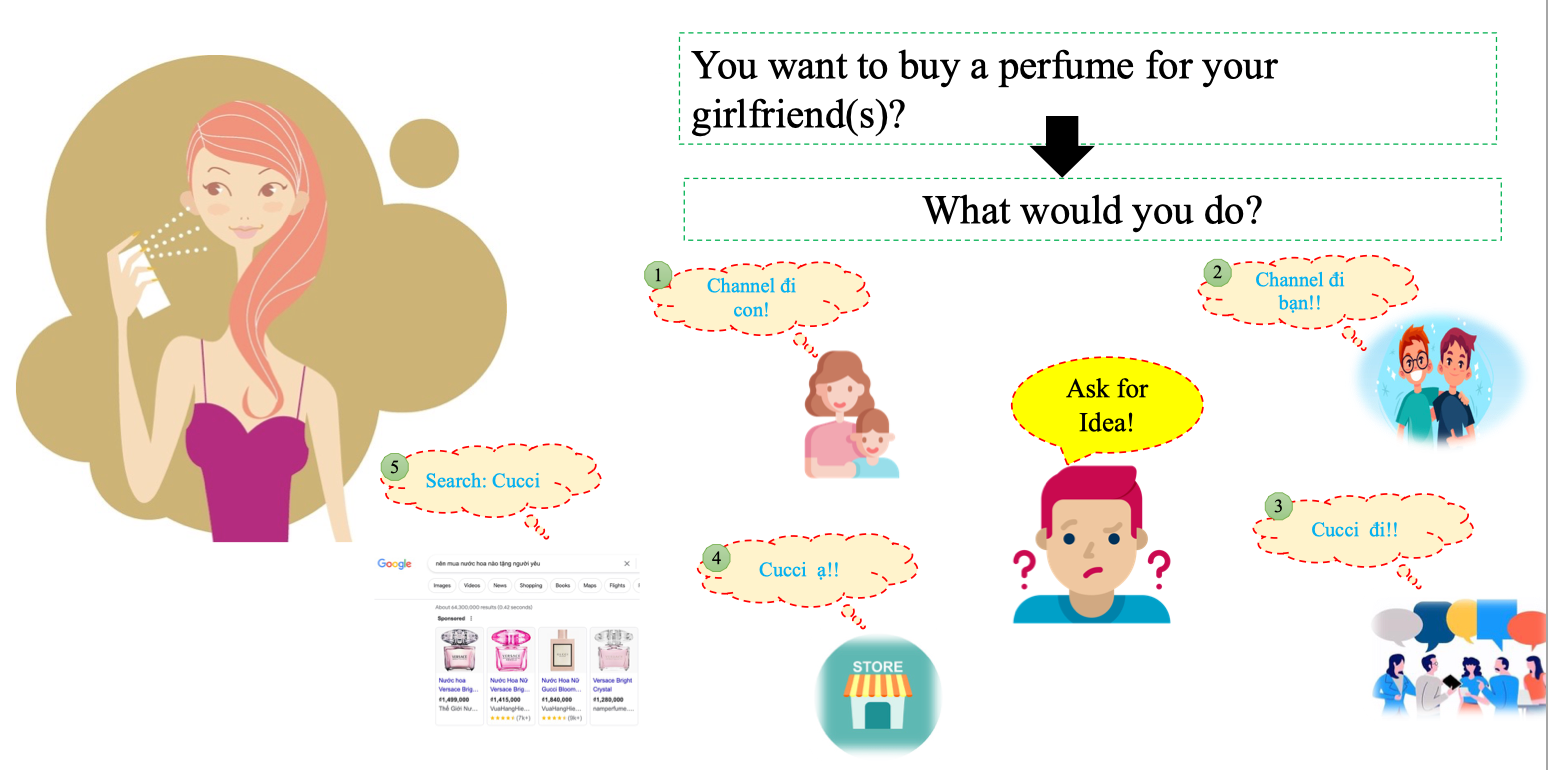
Qua các ví dụ khác, ta thấy một Decision Tree đơn lẻ thường được gọi là weak learner vì dễ mắc bias hoặc variance cao. Ý tưởng: thay vì dựa vào một cây duy nhất, ta xây dựng nhiều cây quyết định khác nhau, sau đó kết hợp kết quả để tạo ra mô hình mạnh hơn. Ví dụ: Giả sử bạn muốn mua một chai nước hoa cho bạn gái, nhưng không biết chọn loại nào. Bạn sẽ làm gì? image 13 16.png

  • Hỏi mẹ: “Channel đi con!”
  • Hỏi bạn bè: “Channel đi bạn!!”
  • Hỏi đồng nghiệp: “Cucci đi!!”
  • Hỏi người bán hàng: “Cucci ạ!!”
  • Tự tìm kiếm trên Google: “Search: Cucci” Mỗi nguồn đưa ra một gợi ý khác nhau. Nếu bạn chỉ nghe theo một người (ví dụ mẹ, hoặc đồng nghiệp) thì rất có thể lựa chọn bị thiên lệch (overfitting). Ý tưởng Random Forest:
  • Thay vì dựa vào một lời khuyên đơn lẻ, bạn tổng hợp nhiều ý kiến khác nhau.
  • Nếu đa số đều gợi ý “Cucci” → bạn sẽ chọn “Cucci”.
  • Nếu đa số gợi ý “Channel” → bạn sẽ chọn “Channel”. → Đây chính là nguyên lý voting/averaging trong Random Forest.

2.2. Ensemble learning

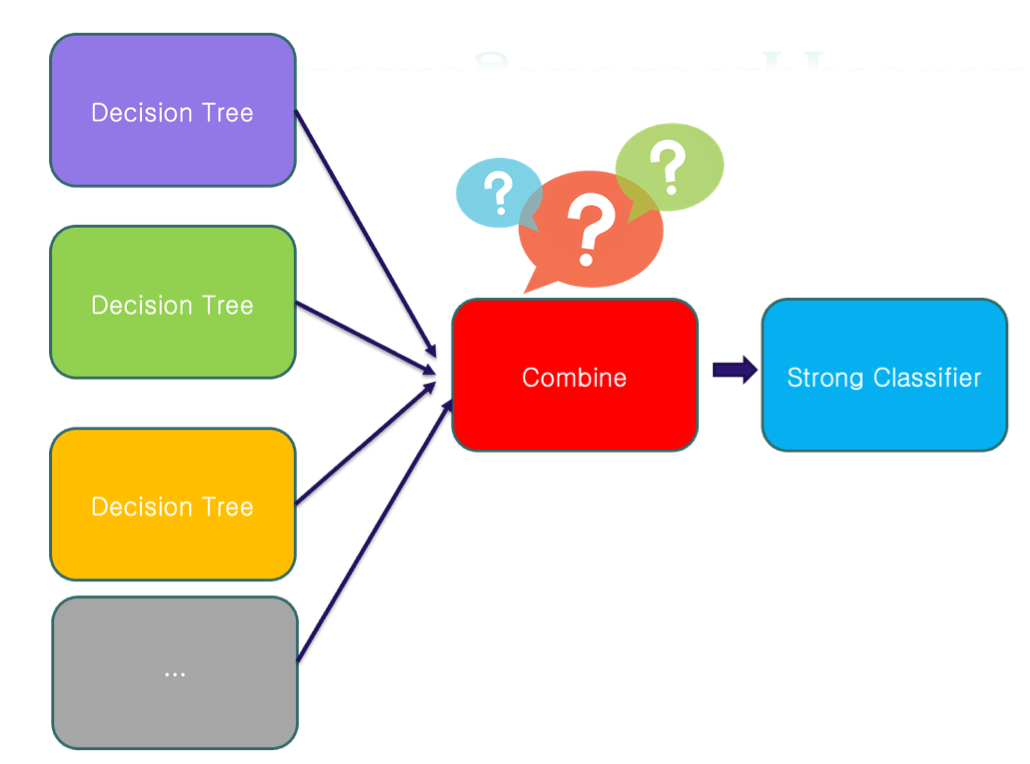
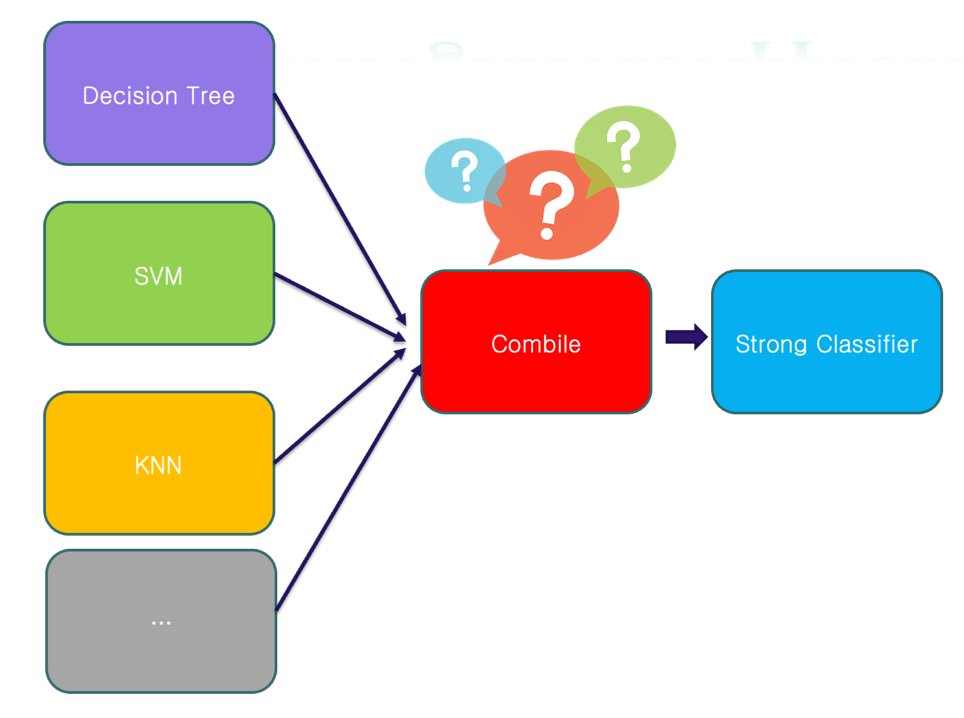
Ensemble Learning = kỹ thuật kết hợp nhiều mô hình yếu (weak classifiers/weak learners) để tạo ra một mô hình mạnh (strong classifier).

  • Weak classifier: mô hình đơn lẻ, thường chỉ dự đoán tốt hơn ngẫu nhiên một chút.
  • Combine: tổng hợp các kết quả của nhiều weak classifiers (voting/averaging/boosting).
  • Strong classifier: mô hình cuối cùng với hiệu năng cao và khả năng tổng quát tốt. Ví dụ:
  • Bagging (Bootstrap Aggregating) → Random Forest.
  • Boosting → AdaBoost, Gradient Boosting, XGBoost.

Homogenous Approach (kết hợp đồng nhất)

Ví dụ: Dùng cùng một thuật toán Decision Tree image 14 16.png

Heterogeneous Approach (kết hợp không đồng nhất)

Kết hợp nhiều thuật toán image 15 16.png

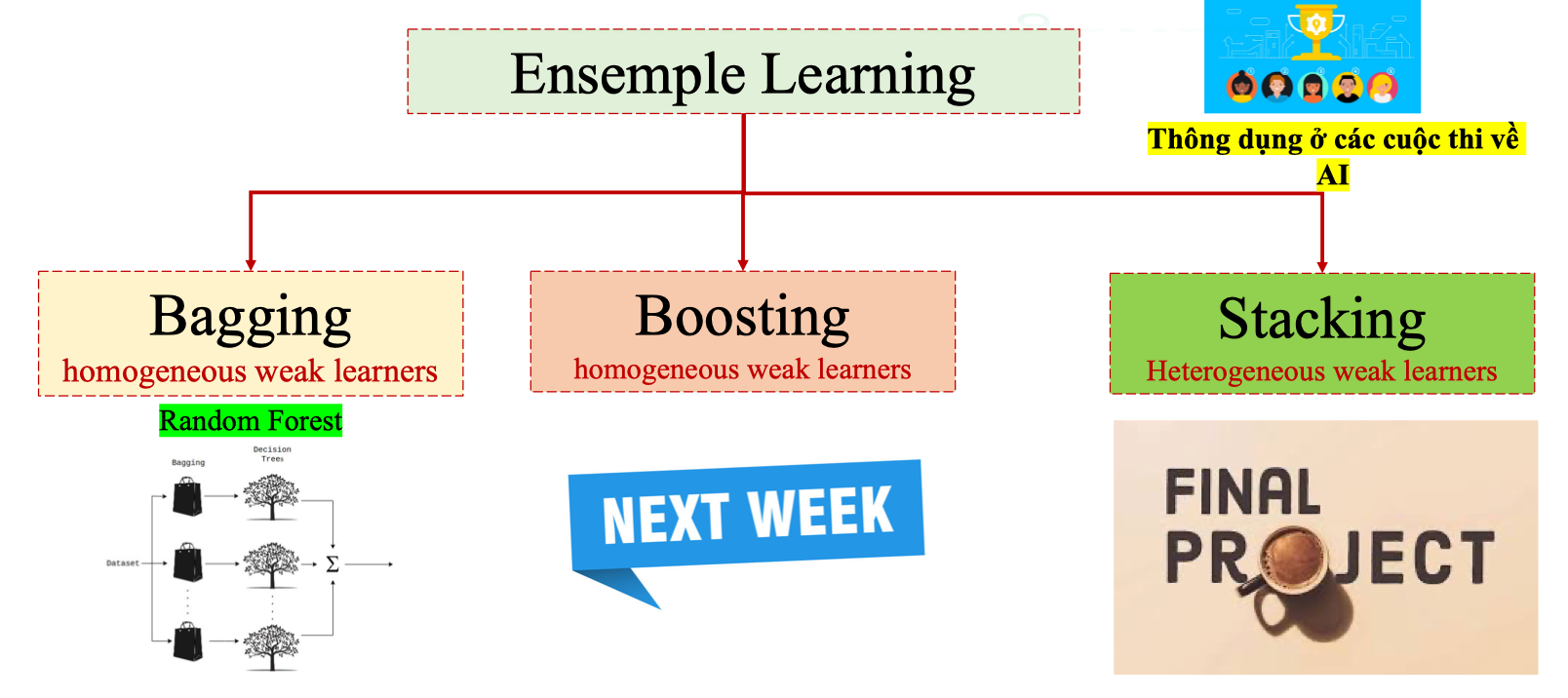
Ensemble Learning Techniques

Có ba hướng chính: Bagging, Boosting, Stacking. image 16 13.png

Bagging (Bootstrap Aggregating)

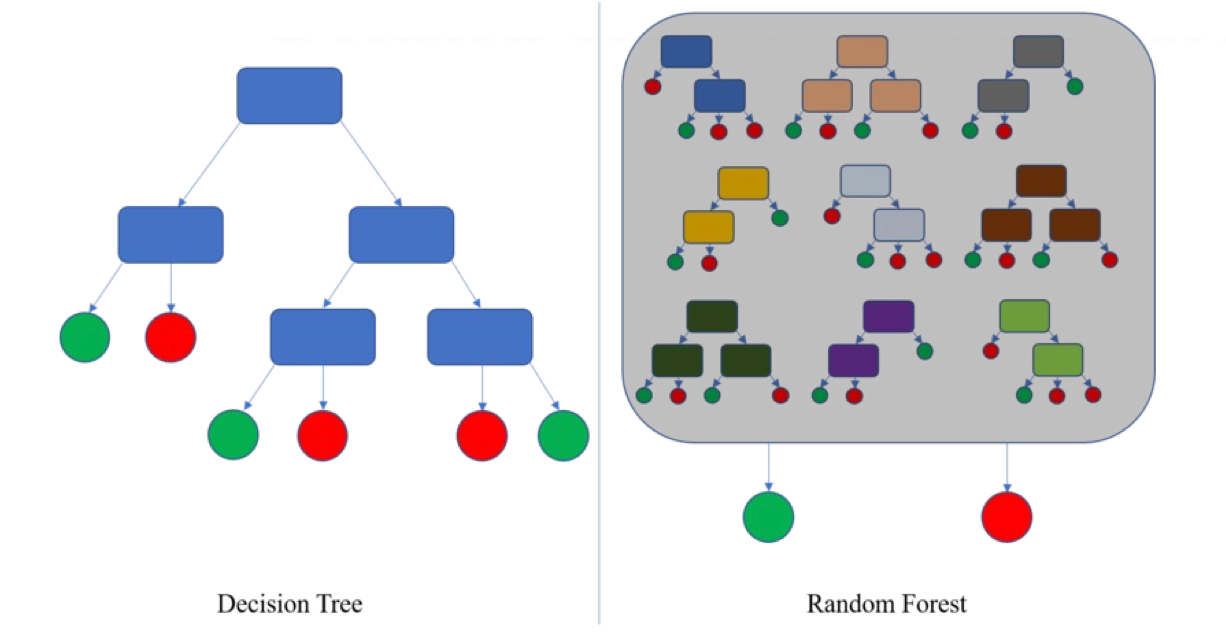
image 17 13.png

  • Weak learners đồng nhất (homogeneous): thường là Decision Trees.
  • Nguyên lý:
    1. Tạo nhiều tập con dữ liệu bằng bootstrap sampling (lấy mẫu ngẫu nhiên có hoàn lại).
    2. Huấn luyện mỗi cây trên một tập con.
    3. Kết hợp kết quả bằng vote (classification) hoặc trung bình (regression).
  • Ví dụ: Random Forest.
  • Ưu điểm: giảm variance, ổn định dự đoán, ít overfitting.

Boosting-Based Method

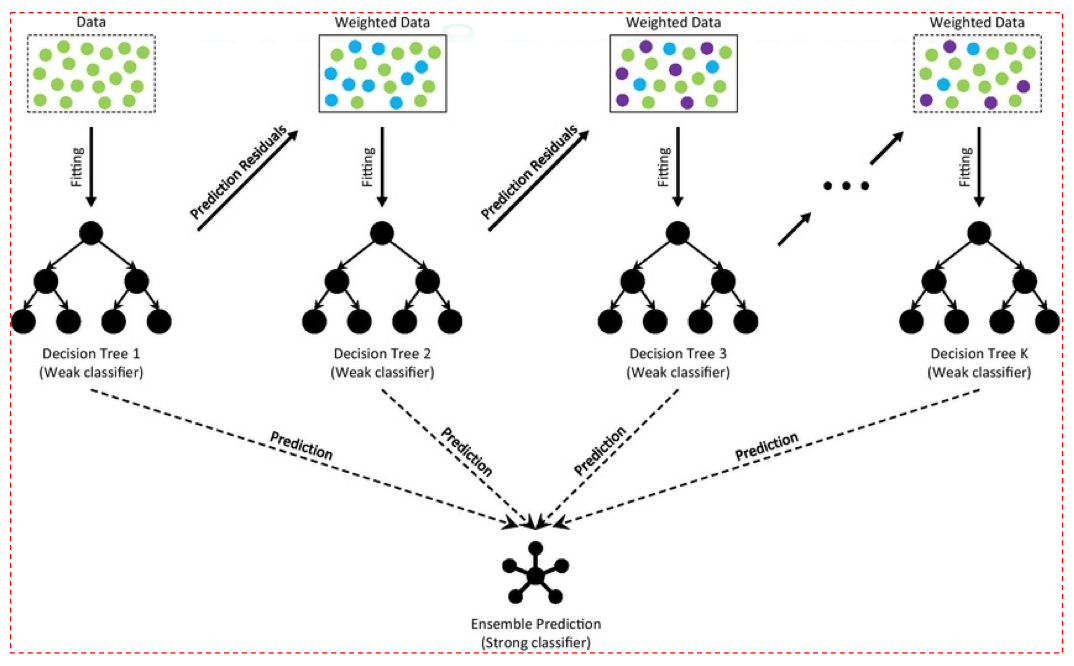
image 18 13.png

  • Weak learners đồng nhất (thường là cây nông).
  • Nguyên lý: huấn luyện tuần tự, mỗi mô hình mới tập trung vào những điểm mà mô hình trước dự đoán sai.
  • Các mô hình Boosting nổi tiếng:
    • AdaBoost
    • Gradient Boosting
    • XGBoost, LightGBM, CatBoost
  • Ưu điểm: giảm cả bias và variance, thường đạt độ chính xác cao.
  • Nhược điểm: dễ overfitting nếu không regularize.

Stacking

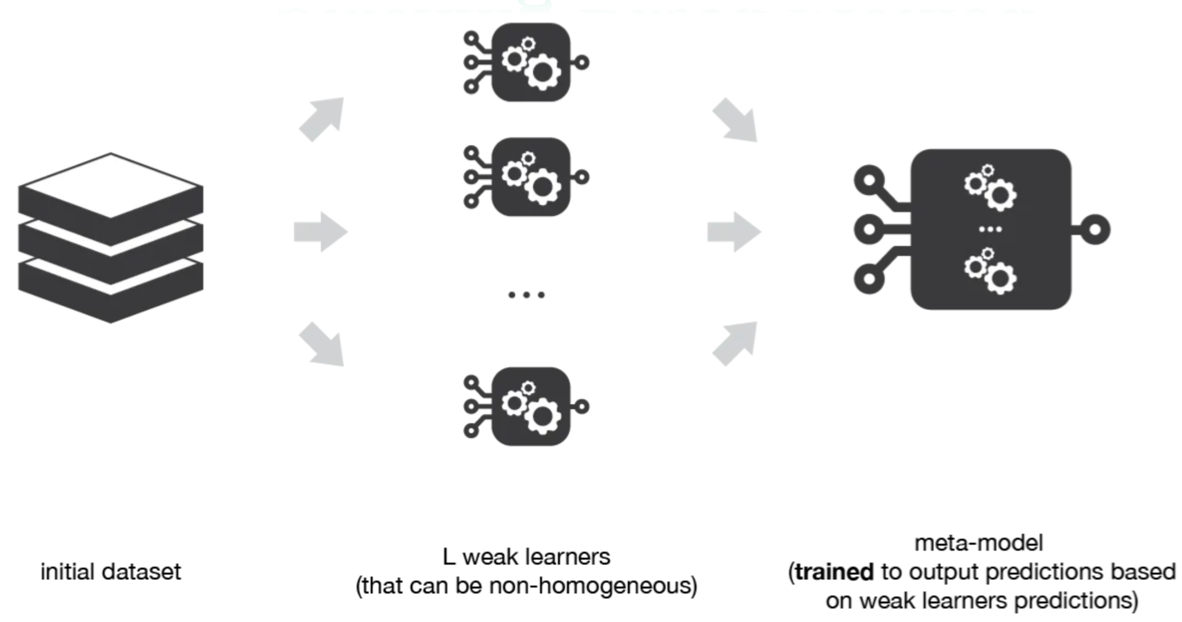
image 19 13.png

  • Weak learners không đồng nhất (heterogeneous): Logistic Regression, SVM, Decision Tree, Neural Network…
  • Nguyên lý:
    1. Huấn luyện nhiều mô hình khác nhau.
    2. Kết quả dự đoán của chúng trở thành đặc trưng đầu vào cho một mô hình “meta-learner”.
    3. Meta-learner học cách kết hợp tối ưu các mô hình gốc.
  • Ứng dụng: rất phổ biến trong các cuộc thi AI/Kaggle vì thường cho kết quả tốt hơn bất kỳ mô hình đơn lẻ nào.

2.3. Build Random Forest

Mô tả Dataset

  • Đây là một bài toán phân loại nhị phân (binary classification).
  • Mục tiêu: Dự đoán bệnh nhân có mắc bệnh tim hay không dựa trên các đặc trưng: đau ngực, tuần hoàn máu, tắc nghẽn động mạch và cân nặng. Bảng dữ liệu có 5 cột đặc trưng và 1 cột nhãn: |Chest Pain|Good Blood Circulation|Blocked Arteries|Weight|Heart Disease (label)| |---|---|---|---|---| |NO|NO|NO|125|NO| |YES|YES|YES|180|YES| |YES|YES|NO|210|NO| |YES|NO|YES|167|YES|
  • Chest Pain (Đau ngực): YES/NO → biến định tính.
  • Good Blood Circulation (Tuần hoàn máu tốt): YES/NO → biến định tính.
  • Blocked Arteries (Động mạch bị tắc nghẽn): YES/NO → biến định tính.
  • Weight (Cân nặng): số (numeric).
  • Heart Disease (Bệnh tim): YES/NO → nhãn (label) cần dự đoán.

Step 1: Create a New Dataset

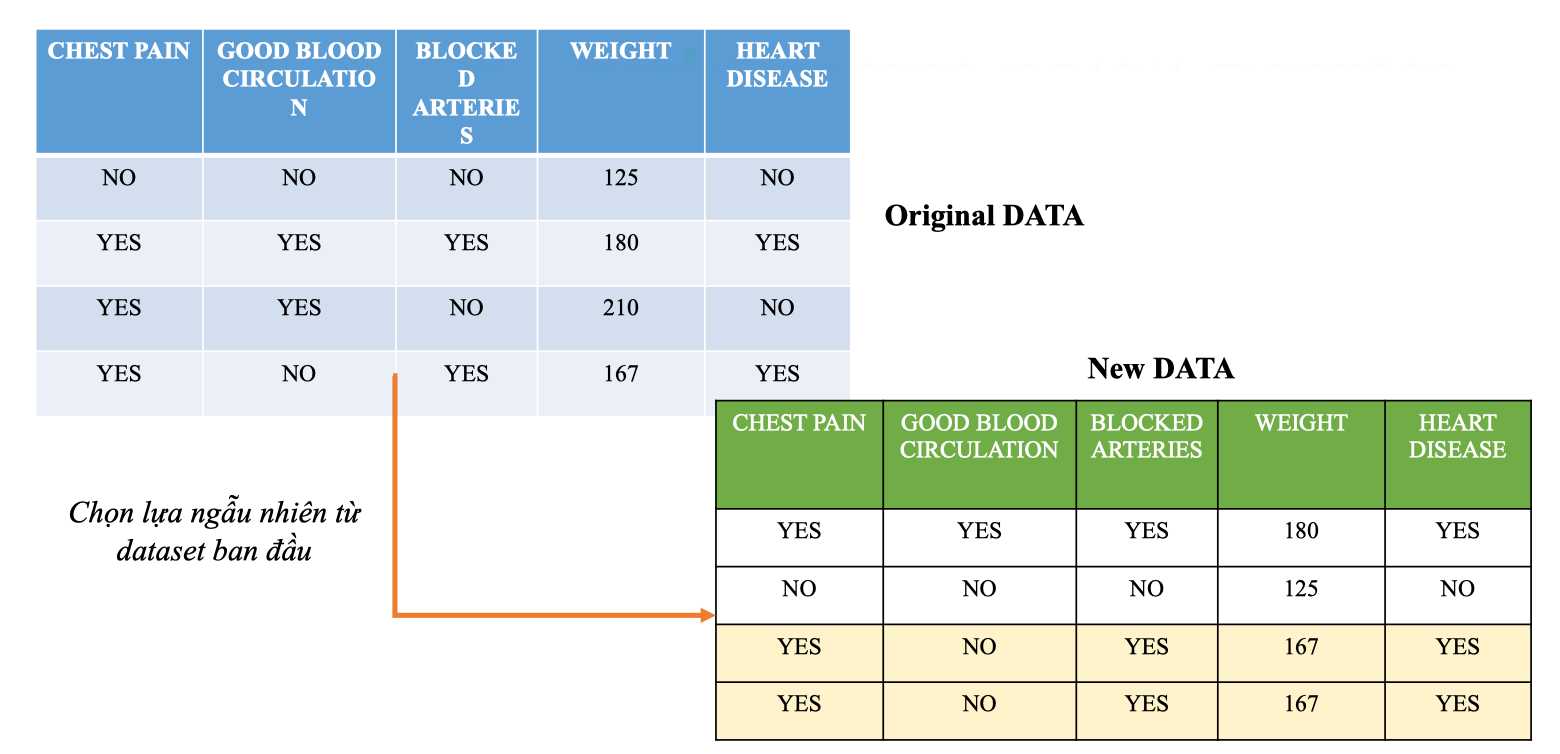
  • Random Forest sử dụng Bootstrap Sampling:
    • Chọn ngẫu nhiên các hàng từ dataset gốc.
    • Chọn có hoàn lại (một mẫu có thể được chọn nhiều lần).
  • Kết quả: tạo ra một New Dataset cho từng cây Decision Tree. image 20 12.png Ta thấy:
  • Mẫu số 2 và số 4 được chọn.
  • Mẫu số 4 bị lặp lại 2 lần. Ý nghĩa:
  • Mỗi cây trong Random Forest sẽ học trên một phiên bản dataset khác nhau.
  • Nhờ đó, các cây trở nên đa dạng và ít tương quan hơn.
  • Khi kết hợp nhiều cây lại (ensemble), mô hình trở nên ổn định và mạnh mẽ hơn. 💡 Tip: Bootstrap sampling không chỉ giúp đa dạng hóa dữ liệu cho từng cây, mà còn hỗ trợ việc đánh giá Out-of-Bag (OOB error) – một kỹ thuật thay thế cross-validation trong Random Forest.

Step 2: Random Feature Selection (Predefined Conditions)

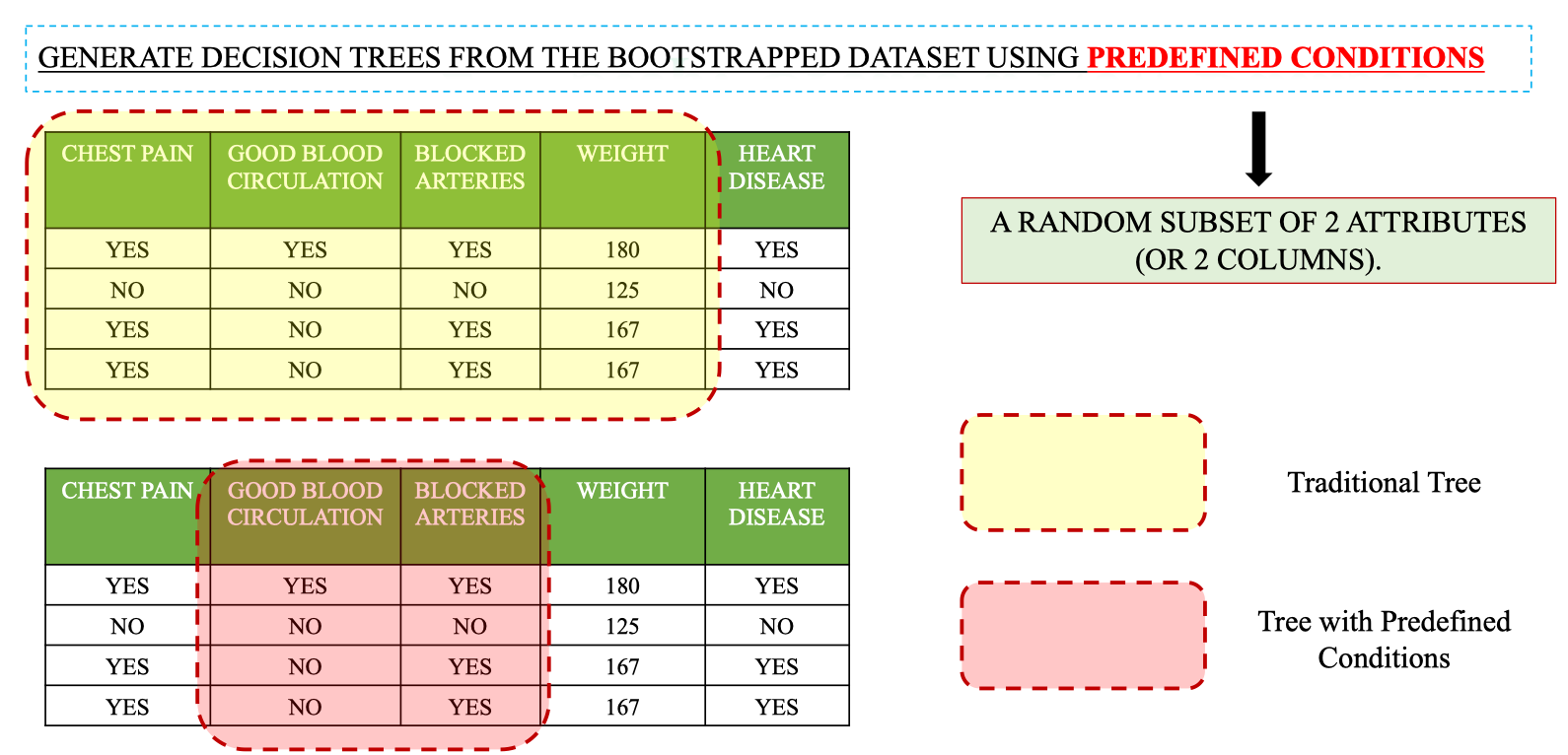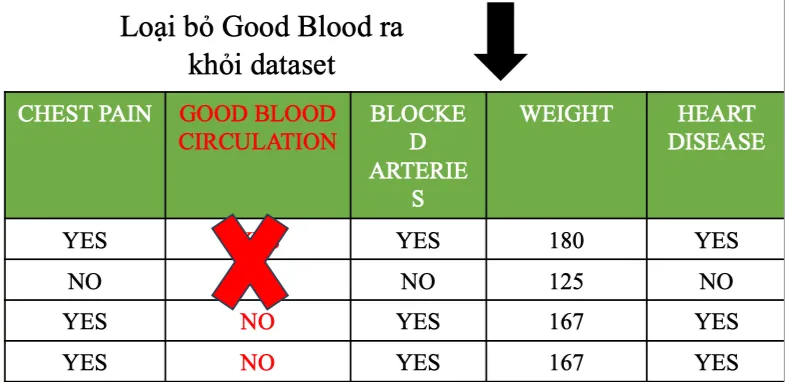
  • Tại mỗi node, chỉ xét một tập con ngẫu nhiên của các feature thay vì toàn bộ. ⇒ Điều này tạo ra sự đa dạng giữa các cây, giảm tương quan, từ đó giảm variance khi kết hợp. Ví dụ: dataset có 4 feature → tại mỗi node chỉ chọn 2 feature ngẫu nhiên để xét. image 21 11.png Đầu tiên tính Gini của hai feature rootnote đã chọn: 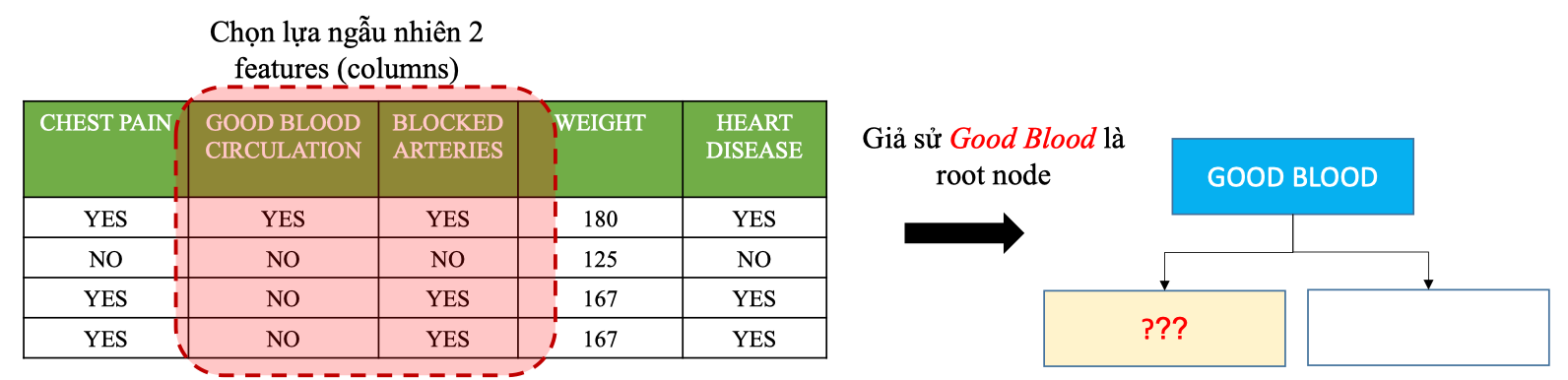image 22 9.png → Giả sử ta chọn Feature: Good Blood Sau đó ta sẽ bỏ Good Blood ra khỏi dataset Nếu không loại bỏ:
  • Vẫn có khả năng bị chọn lại Good Blood → sau đó lại bị overfitting

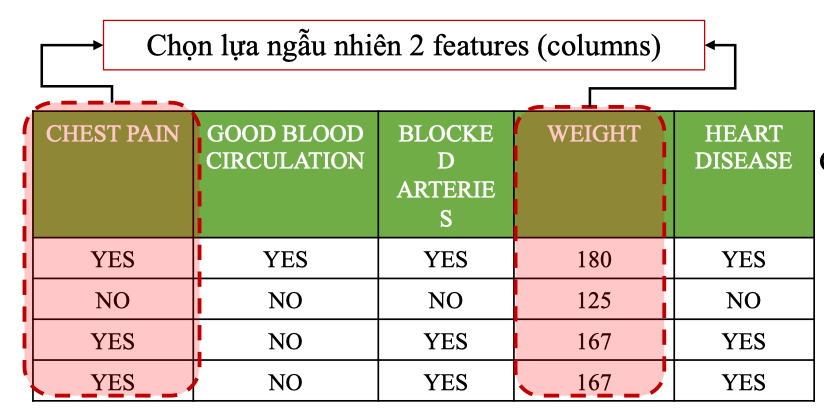image 23 9.png Tiếp tục Chọn lựa ngẫu nhiên 2 Features Dựa trên Gini ta chọn được Chest pain là node tối ưu

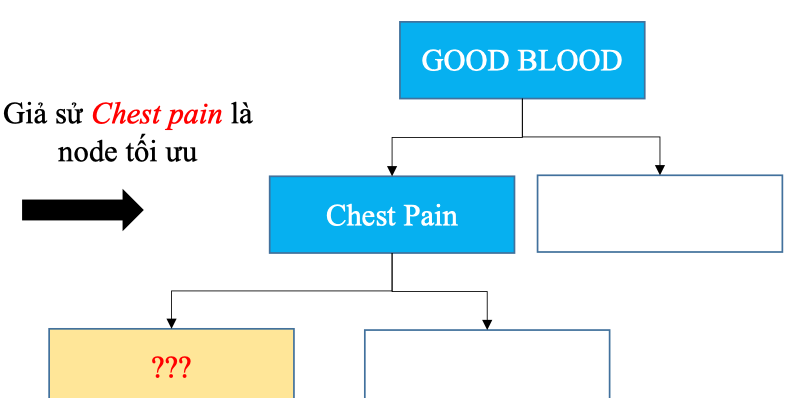
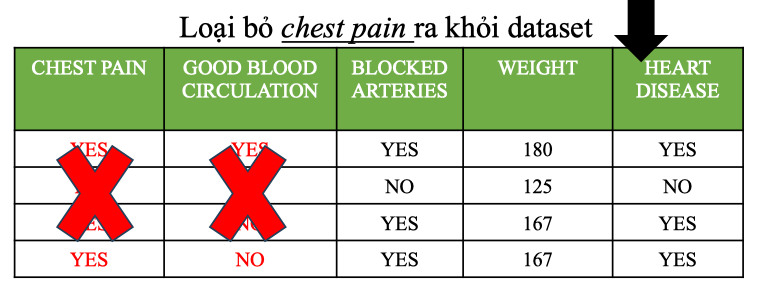image 24 9.png image 25 9.png Sau đó loại bỏ chest pain (thuộc tính đã chọn) ra khỏi dataset.

Lặp lại tiếp tục chọn ngẫu nhiên 2 features

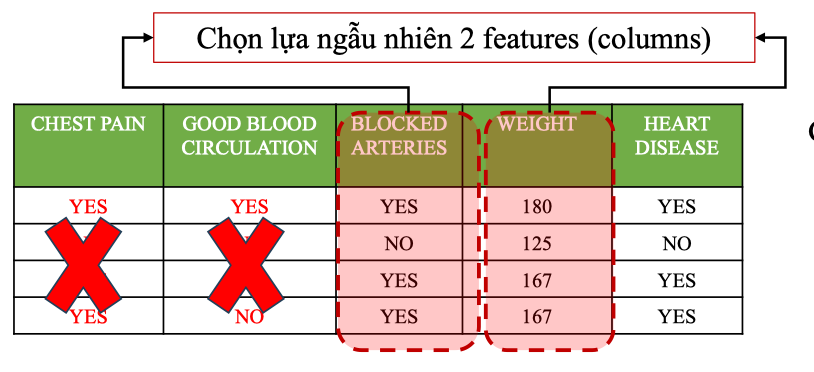image 26 6.png Tiếp tục chọn ra một Feature tối ưu dựa trên Gini, ta sẽ có được cây dưới đây: 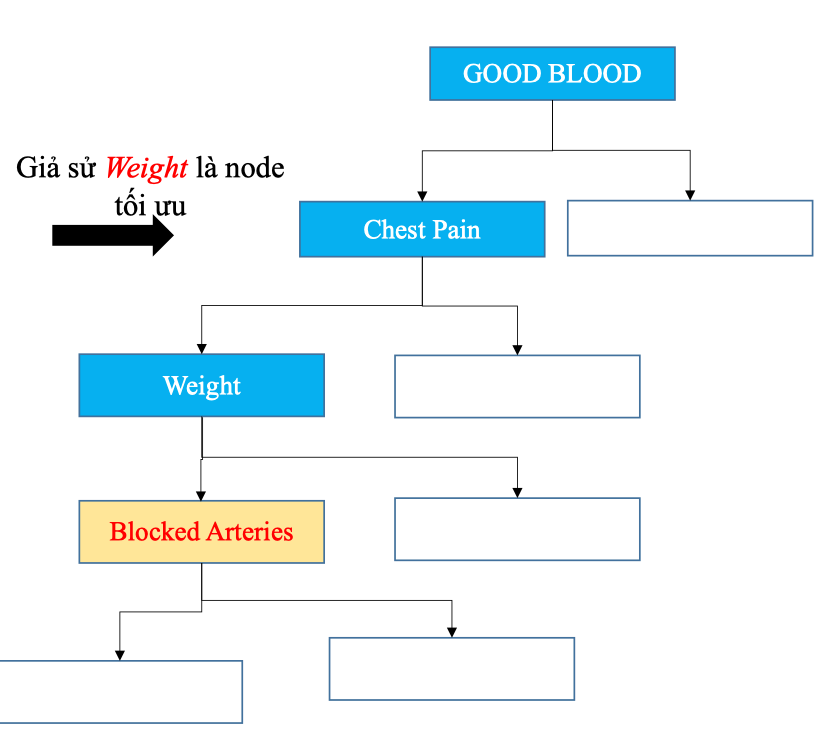image 27 6.png Cứ tiếp tục vậy, chúng ta sẽ tạo ra được một Decision Tree đầu tiên.

Create N Tree

Tiếp đến chúng ta sẽ lặp lại quy trình tạo ra N cây tiếp theo để có được Random Forest. 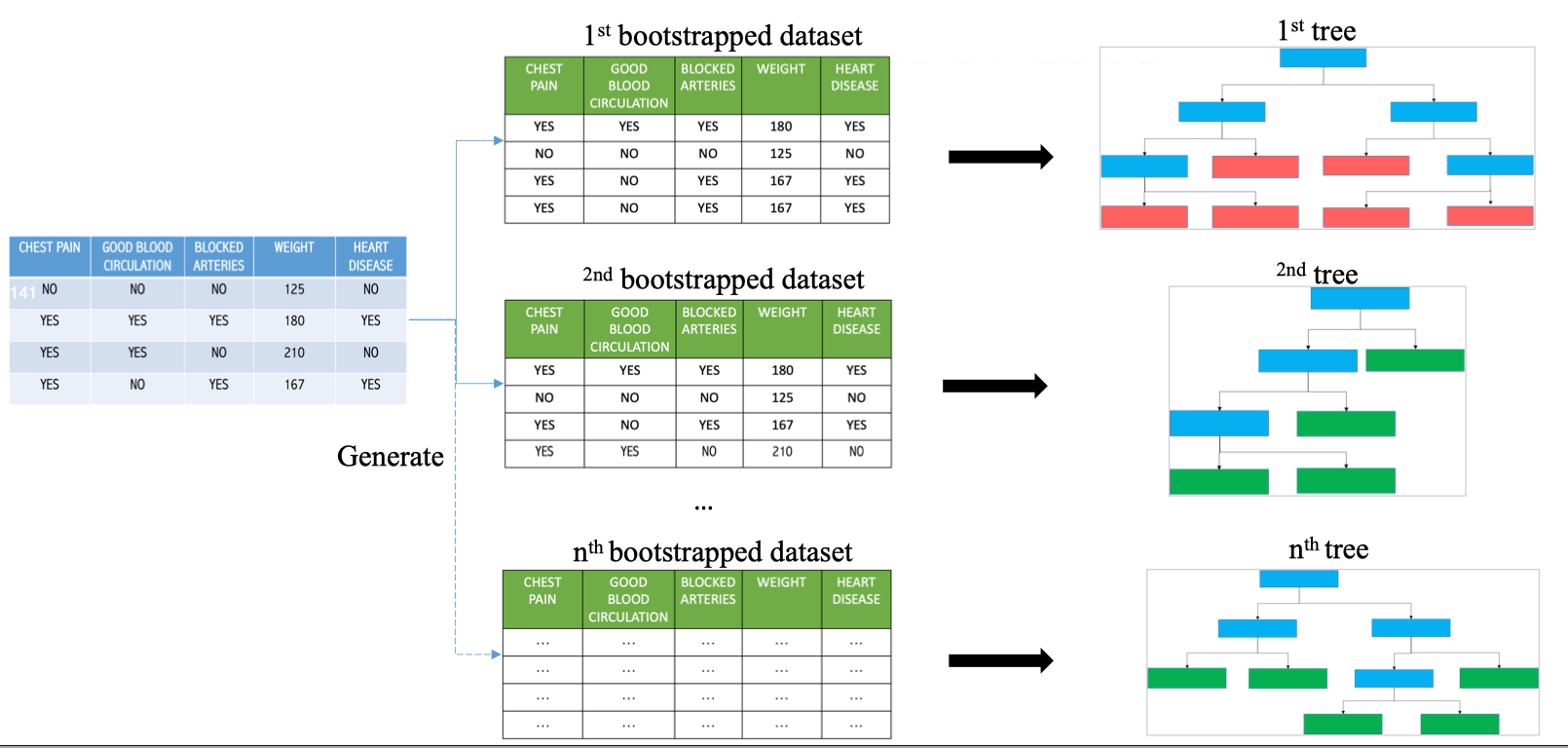image 28 5.png Quá trình sinh nhiều bootstrap datasets:

  • Từ dataset gốc, Random Forest thực hiện bootstrap sampling nhiều lần.
  • Mỗi lần sinh ra một bootstrap dataset (có cùng kích thước nhưng các mẫu được chọn ngẫu nhiên có hoàn lại).
  • Ví dụ:
    • 1st bootstrap dataset khác với 2nd bootstrap dataset vì chọn mẫu khác nhau.
    • Điều này tạo ra đa dạng dữ liệu cho từng cây. Huấn luyện nhiều Decision Trees:
  • Với mỗi bootstrap dataset, Random Forest sẽ huấn luyện một Decision Tree riêng.
  • Các cây:
    • Có cấu trúc khác nhau do dữ liệu khác nhau.
    • Có split khác nhau nhờ cơ chế random feature selection (Step 2).
  • Kết quả: Tập hợp n cây quyết định với đa dạng cao. Ý nghĩa:
  • Thay vì chỉ dựa vào 1 cây duy nhất (dễ bị lệ thuộc dữ liệu), Random Forest dựa vào một rừng cây.
  • Đa dạng về dữ liệu (bootstrap) + đa dạng về đặc trưng (random features) giúp giảm overfitting và tăng tổng quát hóa.

Predict New Sample

Giả sử một bệnh nhân mới có thông tin:

  • Chest Pain = NO
  • Good Blood Circulation = NO
  • Blocked Arteries = NO
  • Weight = 125 Chúng ta sẽ dùng Kỹ thuật Bagging (Bootstrap Aggregating) để dự đoán Random Forest Quy trình dự đoán:
  1. Mẫu bệnh nhân mới được đưa vào từng cây trong Random Forest.
  2. Mỗi cây cho kết quả: YES (có bệnh) hoặc NO (không bệnh).
  3. Random Forest tổng hợp kết quả bằng Majority Voting:
    • Ví dụ:
      • Tree 1: YES
      • Tree 2: YES
      • Tree n: NO
    • Tổng kết: YES = 7, NO = 2 → dự đoán cuối cùng = YES (có bệnh).

Out-of-bag Dataset

Vấn đề của Random Forest là:

  • Khi dùng bootstrap sampling, mỗi cây trong Random Forest chỉ được huấn luyện trên một bootstrap dataset.
  • Vì chọn mẫu có hoàn lại, sẽ có những mẫu bị lặp lại, đồng thời một số mẫu không xuất hiện trong bootstrap dataset.
  • Những mẫu không được chọn này được gọi là Out-of-Bag (OOB) samples. 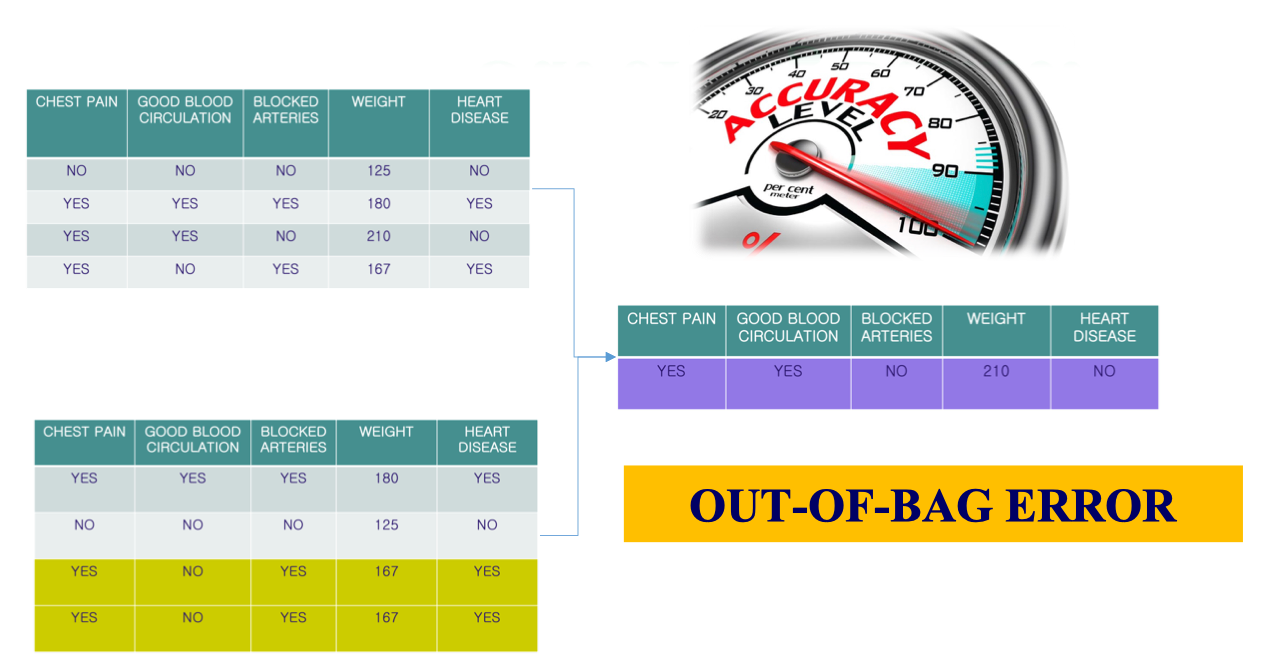image 29 4.png Ý tưởng Out-of-Bag
  • Với mỗi cây, ta có thể dùng các mẫu OOB (không xuất hiện trong tập bootstrap của cây đó) để đánh giá sai số dự đoán.
  • Như vậy, không cần tách thêm tập validation riêng, ta vẫn có thể ước lượng được độ chính xác của Random Forest.

3. Application: Miss data problem

3.1. Random Forest with Missing Data

Random Forest có thể giải quyết bài toán Filling Missing Data khá tốt vì nó đánh giá được dựa trên sự ra quyết định của các cây. image 30 4.png

Type of Missing Data

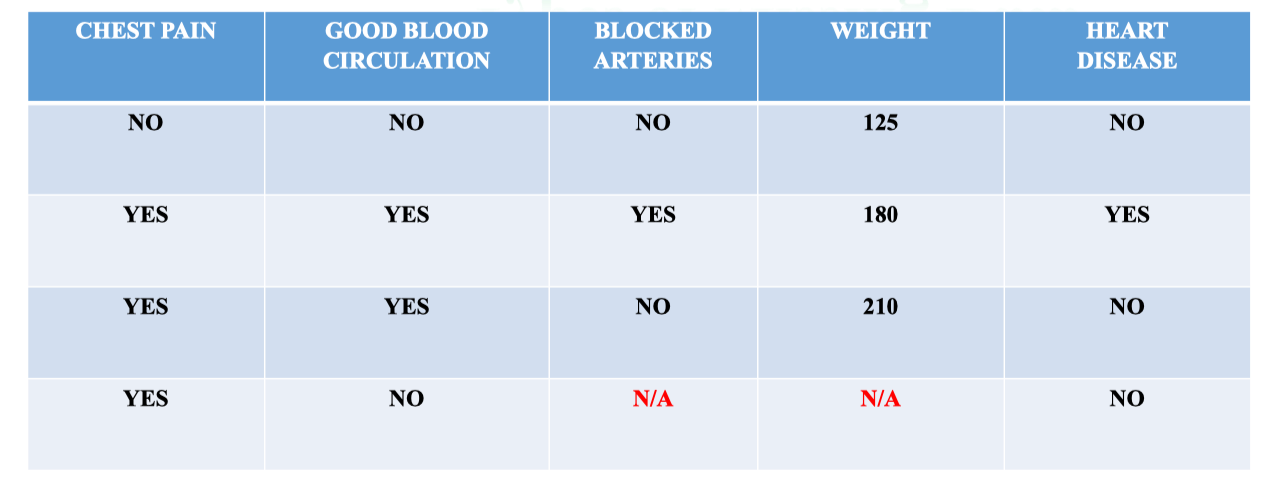
Loại dữ liệu mà Random Forest có thể xử lý là dạng Text (phân loại) và Numbering (số). Đây là một bảng dữ liệu bị missing dữ liệu ví dụ: image 31 4.png

Overview pipeline Fill in Missing Data

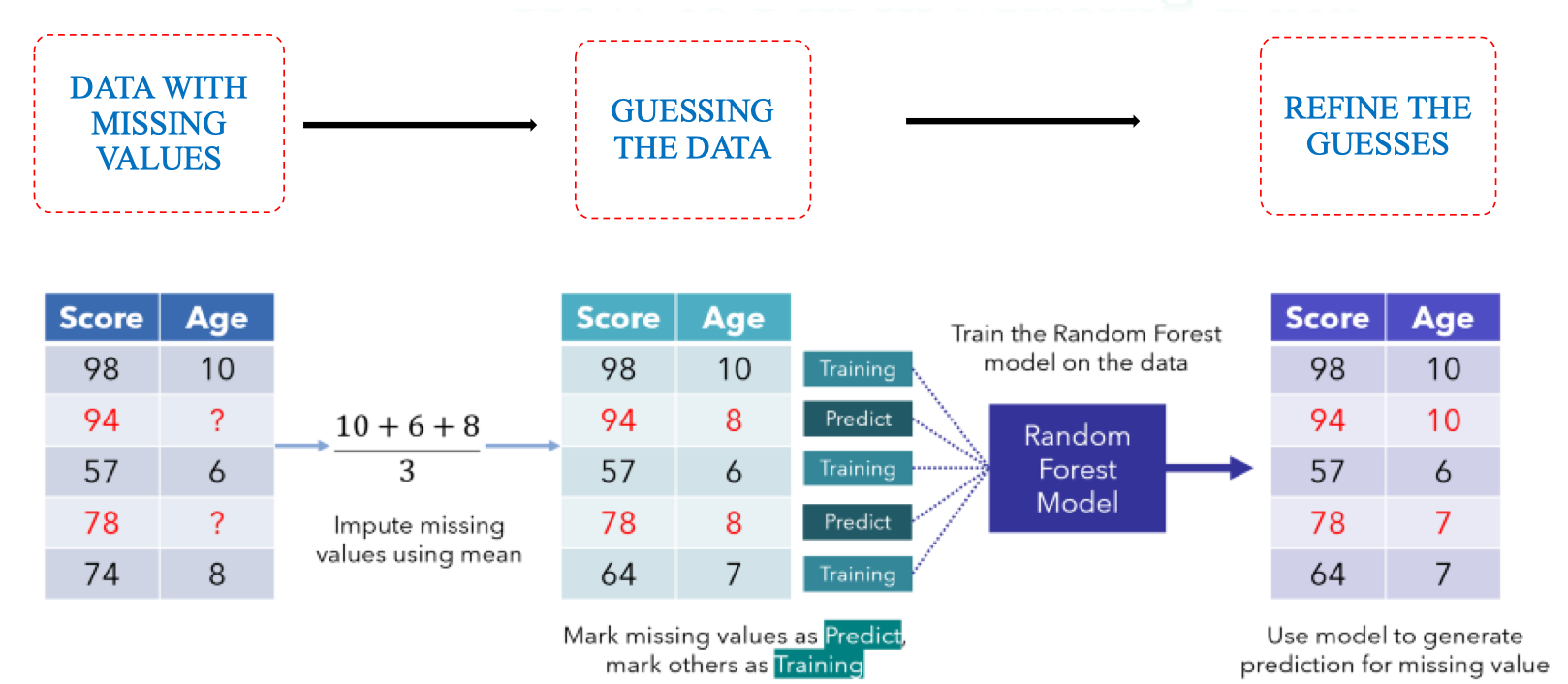
image 32 4.png

Guessing the Data

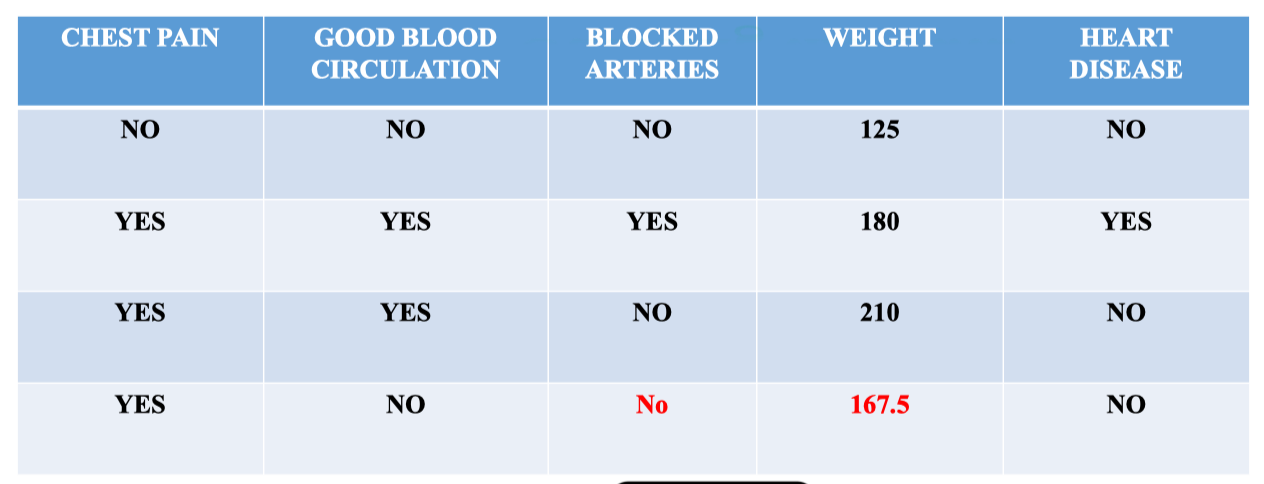
Ý tưởng ban đầu là ta sẽ dự đoán giá trị ban đầu và hiệu chỉnh nó tốt hơn sau này qua RF. Ví dụ ở đây chúng ta sẽ điền là No và 167.5 cho hai vị trí miss của bảng dữ liệu: image 33 4.png

Guessing the Data

Để refine dự đoán ban đầu, chúng ta sẽ xây dựng Random Forest và từ đó cho ra Proximity Matrix để đánh giá trọng số của các mẫu xung quanh dữ liệu thiếu. image 34 4.png

3.2. Proximity Matrix

  • Proximity Matrix là một ma trận vuông dùng để đo mức độ tương đồng giữa các mẫu dữ liệu trong Random Forest.
  • Ý tưởng:
    • Nếu hai mẫu dữ liệu thường xuyên rơi vào cùng một lá (leaf node) trong nhiều cây khác nhau → chúng có tính chất gần nhau.
    • Ngược lại, nếu chúng hiếm khi cùng lá → khoảng cách xa hơn.

Cách xây dựng Proximity Matrix

  1. Bắt đầu với ma trận vuông n x n (n = số mẫu).
  2. Với mỗi cây trong rừng:
    • Nếu mẫu i và j cùng rơi vào cùng lá, tăng giá trị Proximity[i][j] lên 1.
  3. Sau khi xét tất cả cây, chia các giá trị trong ma trận cho tổng số cây để chuẩn hóa về khoảng [0,1]. Ví dụ
  • Dataset có 4 mẫu.
  • Khi qua Tree 1:
    • Mẫu 3 và mẫu 4 cùng rơi vào một lá → đánh dấu Proximity[3][4] = 1 và Proximity[4][3] = 1.
  • Các ô khác để trống (hoặc = 0).
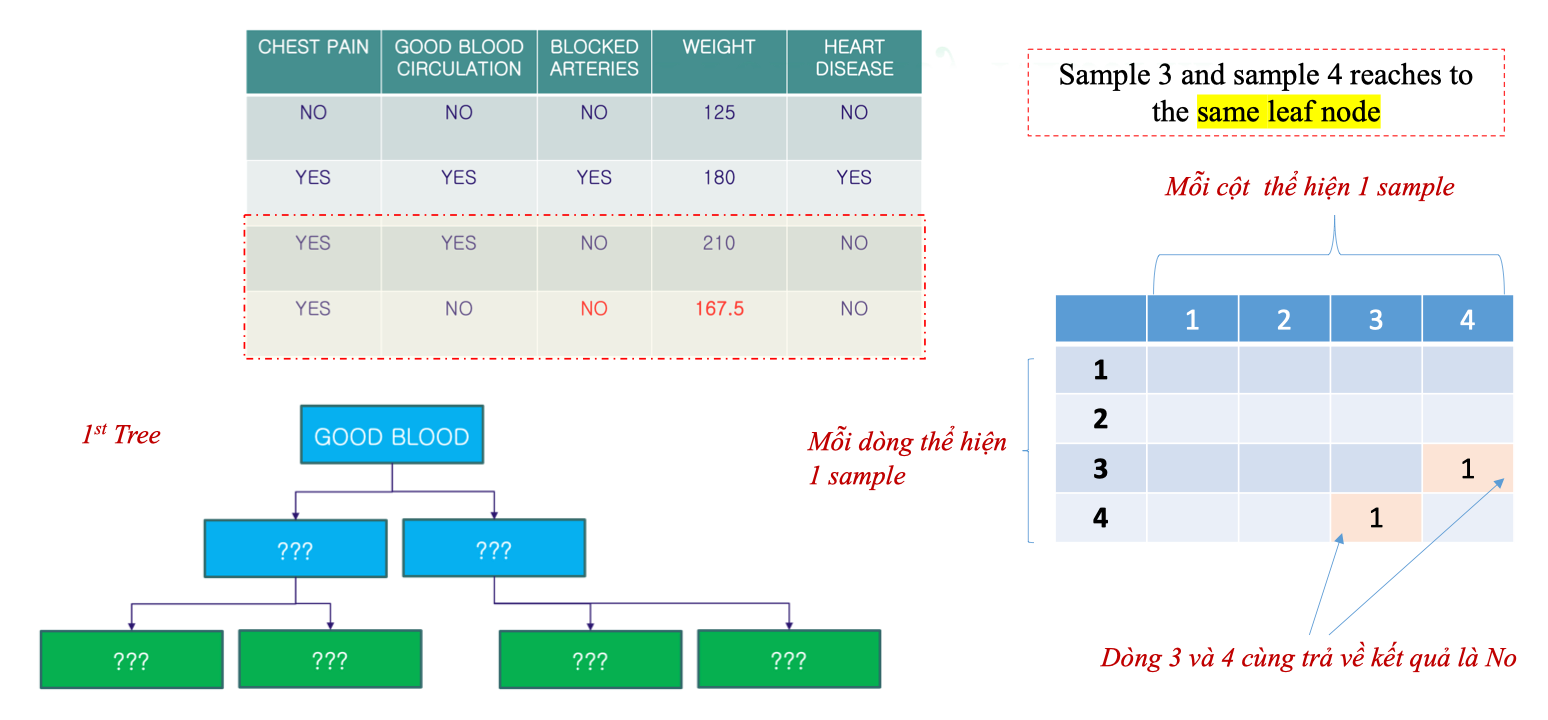
  • Kết quả: ma trận thể hiện mức độ gần gũi giữa các cặp mẫu. image 35 4.png
  • Tree 2:
    • Mẫu 3 và 4 cùng lá → Proximity[3,4] tăng lên 2.
    • Mẫu 2 và 3 cùng lá → Proximity[2,3] = 1.
    • Mẫu 2 và 4 cùng lá → Proximity[2,4] = 1.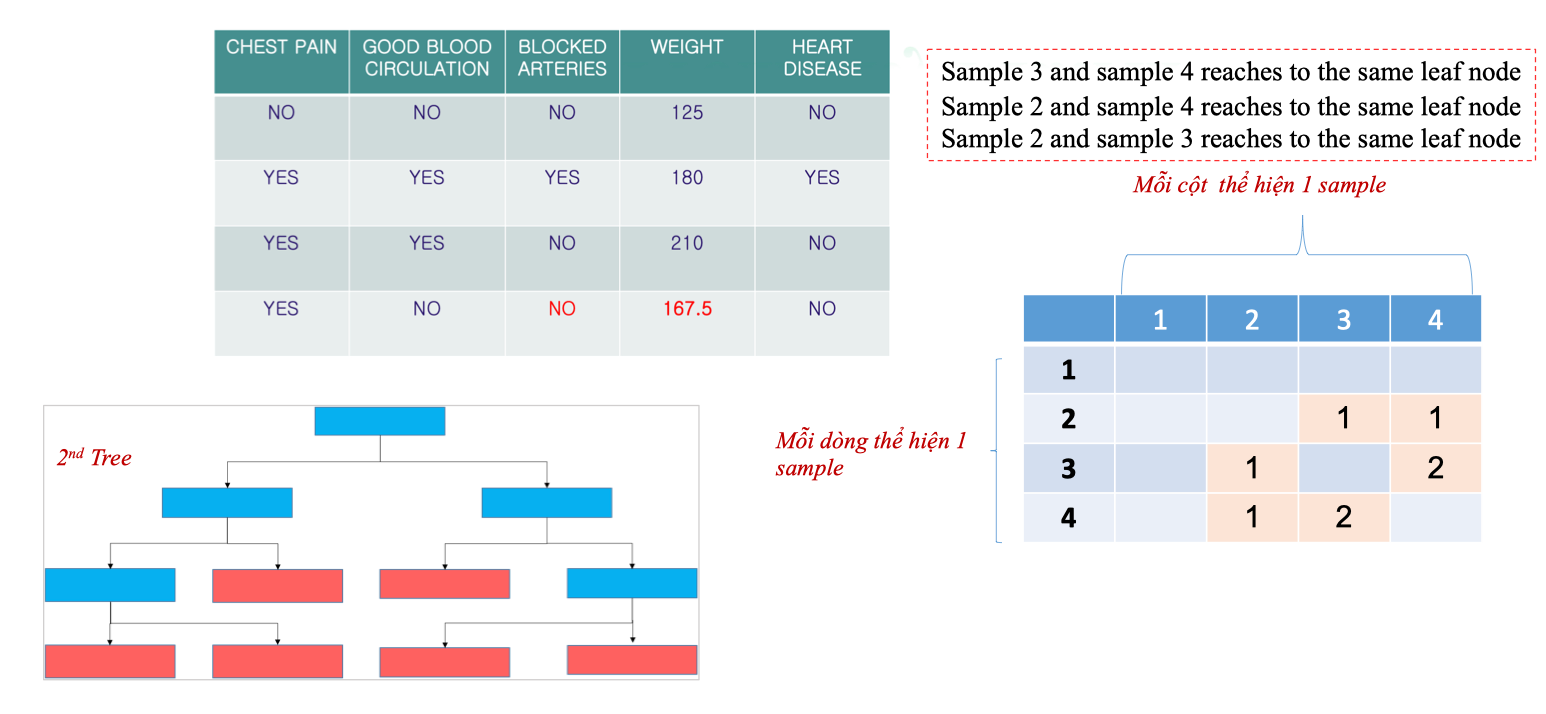 image 36 4.png
  • Sau khi chạy qua nhiều cây:
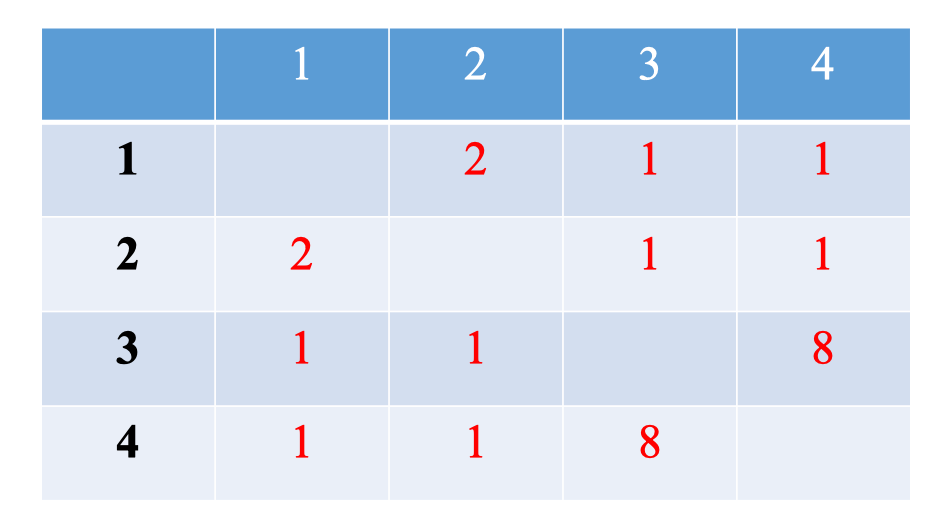
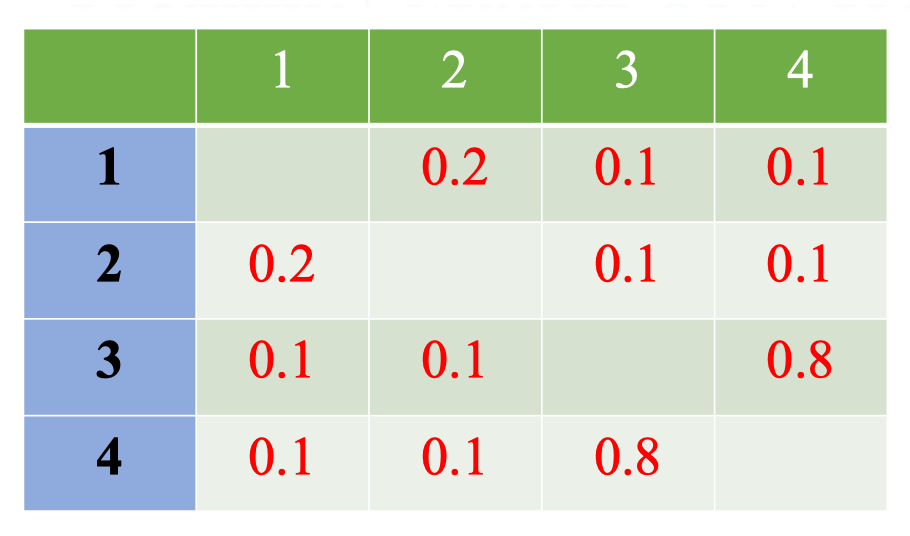
    • Ta Normalization (Chuẩn hóa) Proximity Matrix giả sử ở đây có 10 cái cây. image 37 3.png image 38 2.png

Fill in the Missing Values

  • Proximity Matrix biểu diễn độ “gần gũi” (similarity) giữa các mẫu.
  • Ví dụ: với mẫu số 4, ta thấy:
    • Gần với sample 1: 0.1
    • Gần với sample 2: 0.1
    • Gần với sample 3: 0.8 → Điều này có nghĩa sample 4 “giống” sample 3 nhiều hơn so với các sample khác.

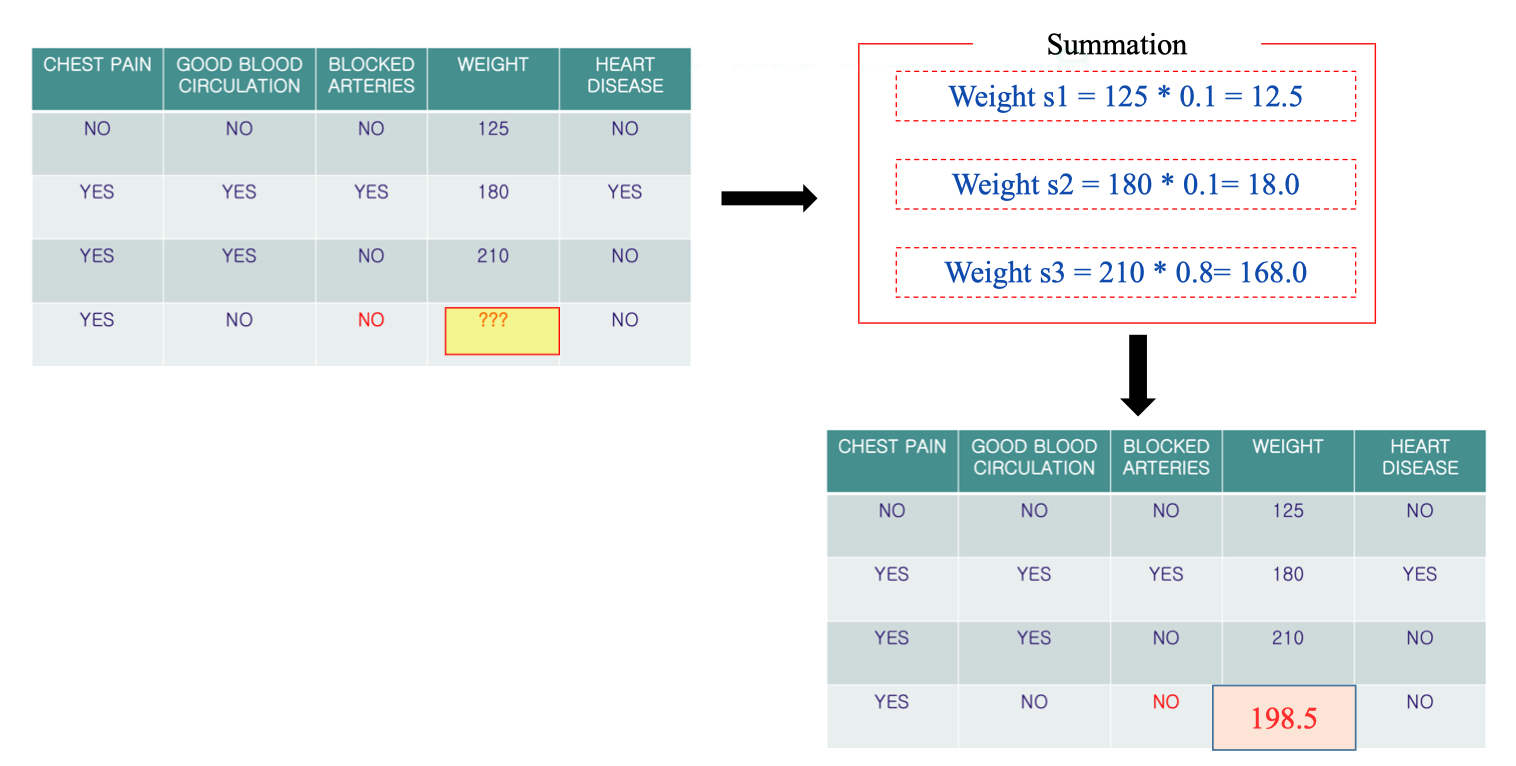
Tính toán Weight Frequency Để điền giá trị thiếu, Random Forest tính toán tần suất có trọng số (weight frequency) của từng giá trị có thể xảy ra dựa trên Proximity Matrix:

  • Ví dụ với Blocked Arteries:
    • Trong các sample (1, 2, 3), có 1/3 mẫu là “YES”.
    • Proximity của sample 4 với mẫu có “YES” = 0.1.
    • Weight frequency của YES = (1/3) × 0.1 = 0.03.
  • Proximity chuẩn hóa (Normalization):
    • Tổng tất cả proximity = 0.1 + 0.1 + 0.8 = 1.0.
    • Nhờ đó có thể tính trọng số xác suất của từng giá trị:

Dự đoán giá trị của Blocked Arteries (dữ liệu phân loại)

  • The weight frequency of Yes = Frequency of Yes * Weight for Yes

    The weight frequency of Yes = 1/3 * 0.1 = 0.03

  • The weight frequency of No = Frequency of No * Weight for No

    The weight frequency of No = 2/3 * 0.9 = 0.6

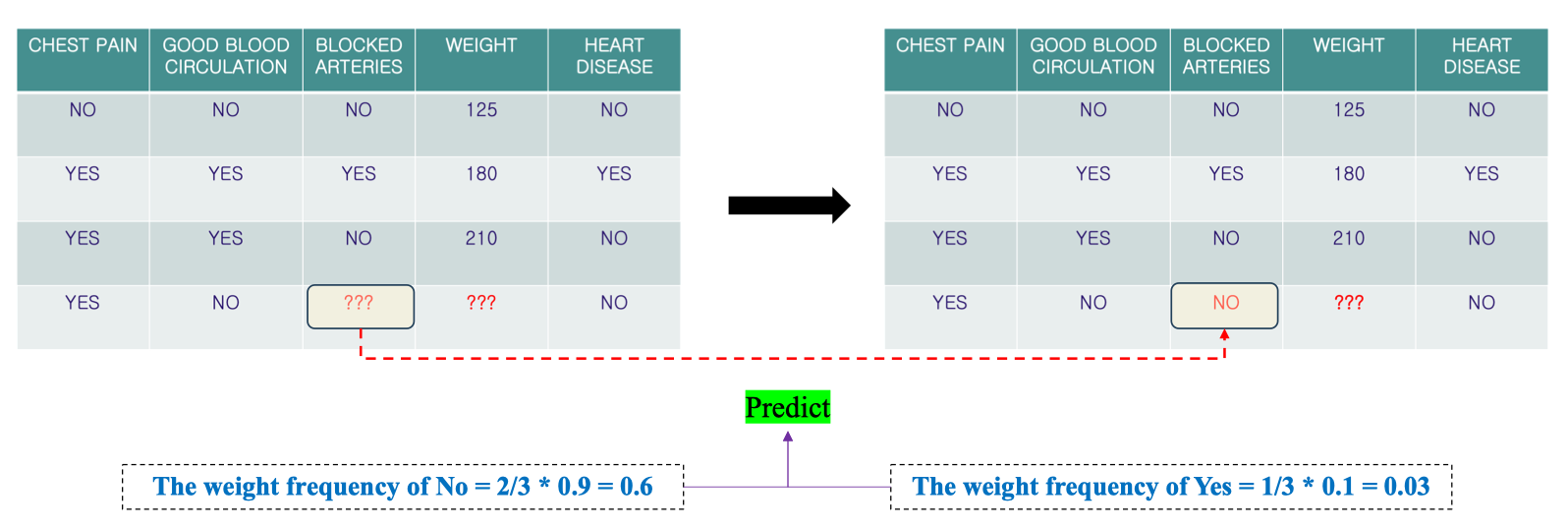image 39 2.png ⇒ Từ đây chúng ta sẽ điền No vào Missing Value.

Dự đoán giá trị của Weight (dữ liệu số)

  • Xác định độ gần (proximity) của sample 4 với các sample khác (dựa vào Proximity Matrix):
    • Với sample 1: 0.1
    • Với sample 2: 0.1
    • Với sample 3: 0.8
  • Nhân giá trị Weight của từng sample với độ gần (proximity):
    • Sample 1:
    • Sample 2:
    • Sample 3:
  • Cộng các giá trị lại:
  • Kết quả: Giá trị thiếu của Weight (sample 4) được điền thành 198.5. image 40 2.png

4. Time Series vs Supervised Learning

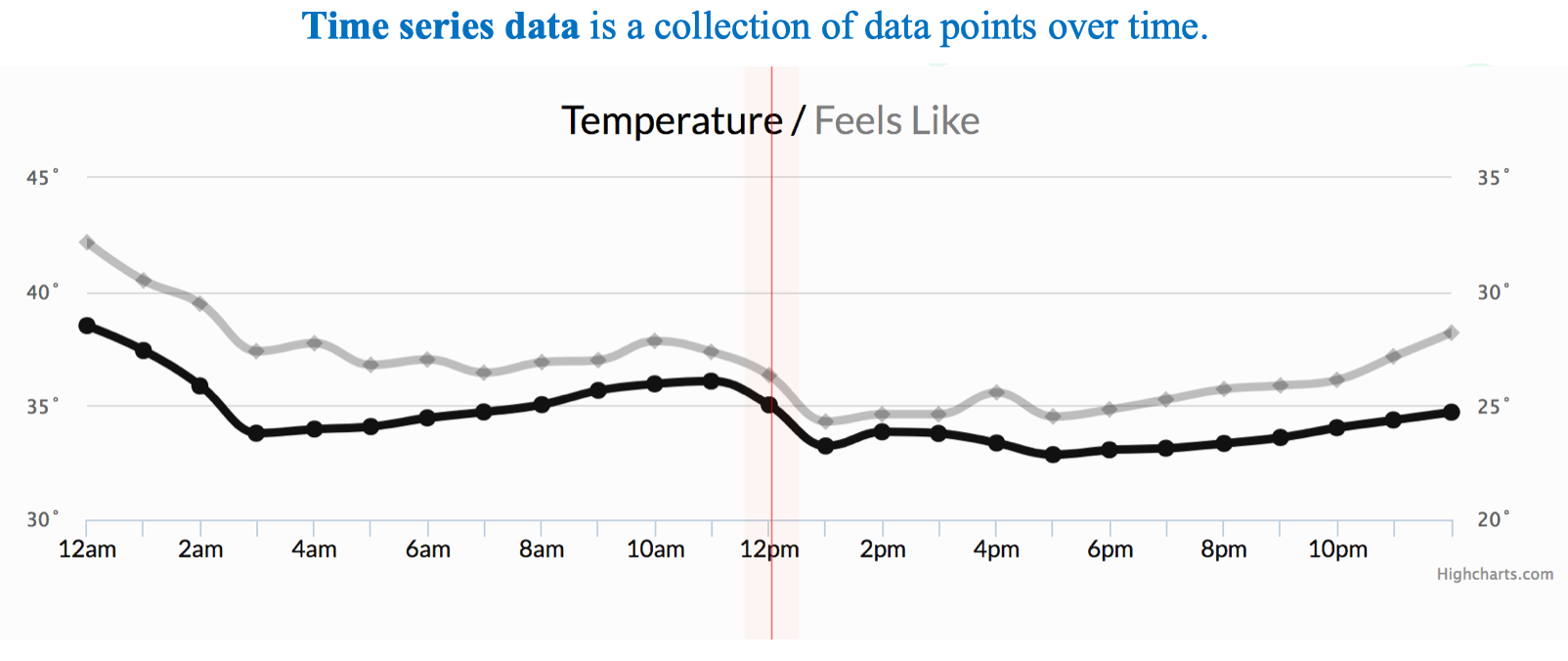image 41 2.png Time series: là chuỗi các giá trị theo thời gian, ví dụ:

t:   1,  2,  3,  4,  5  
y: 100, 110, 108, 115, 120

→ Đây chỉ là dãy số liệu, chưa ở dạng input–output.

Để huấn luyện mô hình, ta cần cặp (X, y):

  • X (input): giá trị ở thời điểm trước.
  • y (output): giá trị ở thời điểm tiếp theo. Ví dụ với sliding window kích thước 1:
X ,   y
100 , 110
110 , 108
108 , 115
115 , 120

Nghĩa là mô hình học: từ giá trị hiện tại → dự đoán giá trị kế tiếp. Sliding window với multivariate time series image 42 2.png

shift() function

Chúng ta có thể dùng hàm **pandas.shift()** để biến đổi chuỗi thời gian (time series) thành dạng dữ liệu cho bài toán supervised learning: Hàm DataFrame.shift() hoặc Series.shift() được dùng để dịch chuyển dữ liệu lên hoặc xuống theo số hàng chỉ định.

DataFrame.shift(periods=1, freq=None, axis=0, fill_value=None)
  • **periods**: số bước dịch chuyển (mặc định = 1).
    • periods > 0: dịch xuống (giá trị đi xuống dưới).
    • periods < 0: dịch lên (giá trị đi lên trên).
  • **fill_value**: giá trị thay thế cho các ô trống sau khi dịch.
  • **axis**: chọn dịch theo hàng (0) hay cột (1).

Ví dụ: Tạo một bảng dữ liệu time series:

from pandas import DataFrame
df = DataFrame()
df['t'] = [x for x in range(10)]
print(df)
   t
0  0
1  1
2  2
3  3
...
9  9

→ Đây chỉ là chuỗi dữ liệu theo thời gian. Dùng **shift(1)** → tạo cột t-1: Dịch xuống 1 hàng

df['t-1'] = df['t'].shift(1)
print(df)
   t  t-1
0  0  NaN
1  1  0.0
2  2  1.0
3  3  2.0
...
9  9  8.0

Ý nghĩa: mỗi giá trị hiện tại t đi kèm với giá trị quá khứ → Đây chính là cách xây dựng input X = t-1 , output y = t. Dùng **shift(-1)** → tạo cột t+1: Dịch lên một hàng

df['t+1'] = df['t'].shift(-1)
print(df)
   t  t+1
0  0  1.0
1  1  2.0
2  2  3.0
3  3  4.0
...
8  8  9.0
9  9  NaN

Ý nghĩa: mỗi giá trị hiện tại t đi kèm với giá trị tương lai (t+1).
→ Đây là cách xây dựng supervised learning: input X = t, output y = t+1 .

Trong SQL:

Hàm tương tự là **LAG()** hoặc **LEAD()**, dùng để lấy giá trị ở hàng trước hoặc sau trong cùng một bảng.

One-Step Univariate Forecasting

Hàm series_to_supervised() biến đổi chuỗi thời gian thành dạng bảng supervised với:

  • Input (X): các giá trị trong quá khứ (t-1, t-2, …).
  • Output (y): giá trị hiện tại và/hoặc tương lai (t, t+1, …). Dùng để huấn luyện các mô hình Machine Learning hoặc Deep Learning (LSTM, GRU, CNN, v.v.) dự báo chuỗi thời gian.
from pandas import DataFrame
from pandas import concat
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
	n_vars = 1 if type(data) is list else data.shape[1]
	df = DataFrame(data)
	cols, names = list(), list()
	# input sequence (t-n, ... t-1)
	for i in range(n_in, 0, -1):
		cols.append(df.shift(i))
		names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
	# forecast sequence (t, t+1, ... t+n)
	for i in range(0, n_out):
		cols.append(df.shift(-i))
		if i == 0:
			names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
		else:
			names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
	# put it all together
	agg = concat(cols, axis=1)
	agg.columns = names
	# drop rows with NaN values
	if dropnan:
		agg.dropna(inplace=True)
	return agg

  • Giải thích code:

    1. Xác định số biến (features)
    n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
    • Nếu data là list → chỉ có 1 biến.
    • Nếu là mảng nhiều cột → lấy shape[1] để biết số biến.
    • df là DataFrame chứa dữ liệu gốc.
    1. Tạo các cột input (lag features):
    for i in range(n_in, 0, -1):
    cols.append(df.shift(i))
    names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
    • df.shift(i) dịch dữ liệu lùi xuống i bước (tạo ra giá trị tại thời điểm quá khứ).
    • Ví dụ: nếu n_in=3 → tạo ra các cột tại thời điểm t-3, t-2, t-1.
    • names đặt tên cột: var1(t-1), var2(t-2), …
    1. Tạo các cột output (forecast):
    for i in range(0, n_out):
    cols.append(df.shift(-i))
    if i == 0:
        names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
    else:
        names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
    • df.shift(-i) dịch dữ liệu lên i bước (tạo ra giá trị tương lai).
    • Nếu n_out=2 → tạo ra cột tại t và t+1.
    • Tên cột: var1(t), var1(t+1), …
    1. Ghép tất cả cột
    agg = concat(cols, axis=1)
agg.columns = names
    • Ghép các cột input + output lại thành 1 DataFrame hoàn chỉnh.
    1. Xử lý NaN
    if dropnan:
    agg.dropna(inplace=True)
    • Vì khi shift sẽ có hàng bị trống (NaN), nên loại bỏ để dữ liệu sạch. Ví dụ minh họa: One-Step Univariate Forecasting Dữ liệu 1 biến, 1 input, 1 output
values = [x for x in range(10)]
data = series_to_supervised(values)
print(data)
   var1(t-1)  var1(t)
1        0.0        1
2        1.0        2
3        2.0        3
4        3.0        4
5        4.0        5
6        5.0        6
7        6.0        7
8        7.0        8
9        8.0        9

Multi-Step or Sequence Forecasting

Là dự đoán với input là 2 và output là 2:

data = [10, 20, 30, 40, 50]
df = pd.DataFrame(data)
print(series_to_supervised(df, n_in=2, n_out=2))
   var1(t-2)  var1(t-1)  var1(t)  var1(t+1)
2       10.0       20.0       30        40.0
3       20.0       30.0       40        50.0

Multivariate Forecasting

Với 2 biến, input 1, output 1:

  • Tạo dữ liệu:
raw = DataFrame()
raw['ob1'] = [x for x in range(10)]
raw['ob2'] = [x for x in range(50, 60)]
values = raw.values
print(raw)
   ob1  ob2
0    0   50
1    1   51
2    2   52
3    3   53
4    4   54
5    5   55
6    6   56
7    7   57
8    8   58
9    9   59
  • Bảng dữ liệu training:
\#Tiep tuc tu block trên
data = series_to_supervised(values)
print(data)
var1(t-1)  var2(t-1)  var1(t)  var2(t)
1        0.0       50.0        1       51
2        1.0       51.0        2       52
3        2.0       52.0        3       53
4        3.0       53.0        4       54
5        4.0       54.0        5       55
6        5.0       55.0        6       56
7        6.0       56.0        7       57
8        7.0       57.0        8       58
9        8.0       58.0        9       59

Example: Dự đoán số ca sinh bé gái hằng ngày

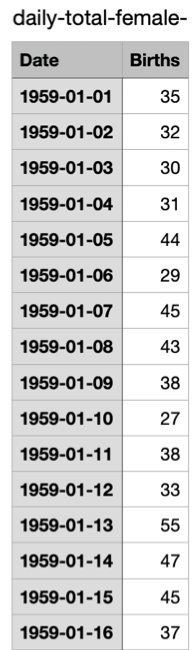image 43 2.png Dữ liệu ghi lại số ca sinh bé gái của 366 ngày từ 01/01/1959. Dataset gốc:
Cột Date (ngày), cột Births (số ca sinh).

# load and plot the time series dataset
from pandas import read_csv
from matplotlib import pyplot
# load dataset
series = read_csv('/content/daily-total-female-births.csv', header=0, index_col=0)
values = series.values
# plot dataset
pyplot.plot(values)
pyplot.show()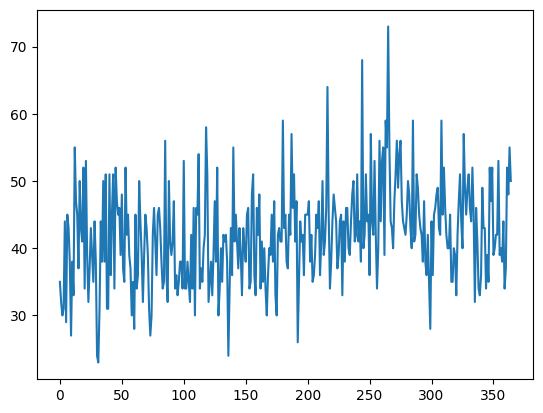

image 44 2.png Bài toán: Dựa vào dữ liệu của n ngày (6 ngày) trước đó, dự đoán số ca sinh ở ngày thứ 7.

series_to_supervised(...) — biến chuỗi thời gian thành dữ liệu học có giám sát

Dựa theo cấu trúc hàm đã xây dựng ở trên ta nhắc lại series_to_supervised(...):

def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
    n_vars = 1 if type(data) is list else data.shape[1]
    df = DataFrame(data)
    cols = list()
    # input sequence (t-n, ... t-1)
    for i in range(n_in, 0, -1):
        cols.append(df.shift(i))
    # forecast sequence (t, t+1, ... t+n)
    for i in range(0, n_out):
        cols.append(df.shift(-i))
    # put it all together
    agg = concat(cols, axis=1)
    # drop rows with NaN values
    if dropnan:
        agg.dropna(inplace=True)
    return agg.values

Tuy nhiên ở đây sẽ return agg.values: trả về NumPy array (không giữ tên cột). Ví dụ: với chuỗi đơn biến , n_in=2, n_out=1 sẽ tạo các hàng:

  • Input → Output
  • , ,

train_test_split(...) — chia train/test theo thời gian

def train_test_split(data, n_test):
    return data[:-n_test, :], data[-n_test:, :]

  • Không xáo trộn (shuffle) để giữ trật tự thời gian.

  • Lấy tất cả trừ n_test hàng cuối làm train, n_test hàng cuối làm test.

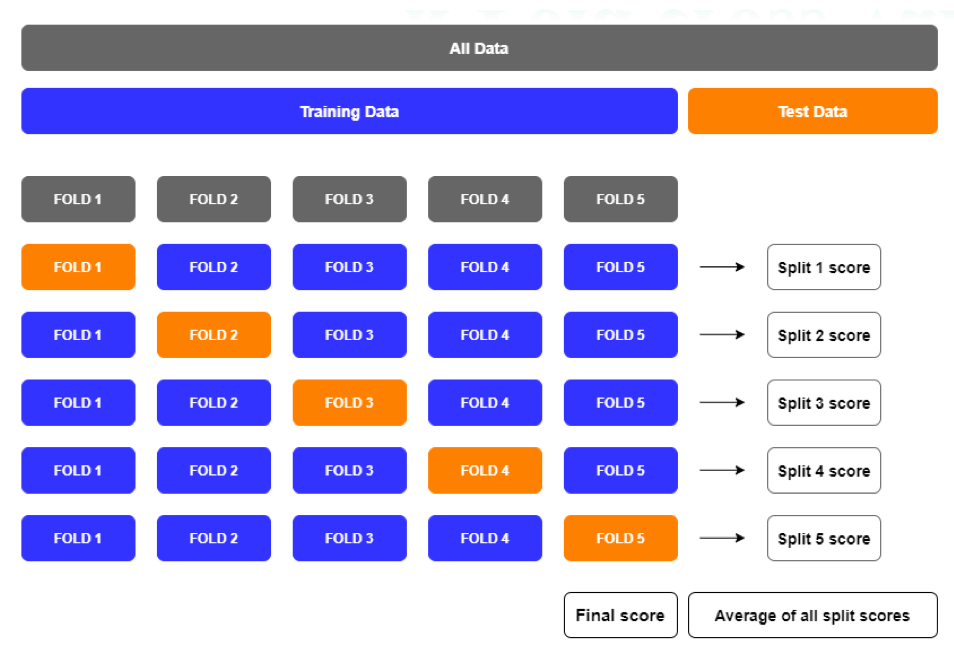
k-Fold cross-validation

  1. Chia dữ liệu

    Dataset được chia thành k phần bằng nhau (gọi là folds).

  2. Chọn tập train và test

    • Mỗi lần lặp (iteration), chọn k-1 folds để train.
    • Fold còn lại làm test.

  3. Huấn luyện mô hình

    Train mô hình trên tập training (k-1 folds).

  4. Đánh giá mô hình

    Dùng fold test để đo lường performance (accuracy, F1, MSE, …).

  5. Lưu kết quả

    Ghi lại metric của lần lặp đó.

  6. Lặp lại k lần

    Mỗi lần đổi fold test → đảm bảo mỗi mẫu trong dataset được dùng làm test đúng 1 lần.

  7. Tính kết quả cuối cùng

    Lấy trung bình các score ở k lần → đây là final score.

image 45 2.png Ưu điểm

  • Giúp giảm bias khi đánh giá mô hình (so với train/test split thông thường).
  • Tận dụng tối đa dữ liệu cho cả huấn luyện và kiểm thử. Nhược điểm
  • Tốn thời gian vì phải train mô hình k lần.

Time Series Cross Validation

Khác với k-Fold CV vì dữ liệu chuỗi thời gian không thể shuffle (phải giữ thứ tự thời gian). Ở đây chúng ta sử dụng kĩ thuật Walk Forward Cross Validation

Rolling Window (Cửa sổ cuộn)

image 46 2.png

  • Kích thước tập train cố định, di chuyển dần theo thời gian.
  • Ví dụ:
    • Split 1: Train (Time1), Test (Time2)
    • Split 2: Train (Time2), Test (Time3)
    • Split 3: Train (Time3), Test (Time4) …
  • Luôn giữ cùng độ dài train, phù hợp khi dữ liệu có tính thời sự, tránh để mô hình “học” quá nhiều từ dữ liệu cũ.

Expanding Window (Cửa sổ mở rộng)

  • Tập train ngày càng mở rộng, chứa tất cả dữ liệu trước đó.
  • Ví dụ:
    • Split 1: Train (Time1), Test (Time2)
    • Split 2: Train (Time1–2), Test (Time3)
    • Split 3: Train (Time1–3), Test (Time4) …
  • Mô hình có “trí nhớ dài hạn”, dùng được tất cả dữ liệu lịch sử.
  • Phù hợp khi dữ liệu không bị lỗi thời, xu hướng quá khứ vẫn hữu ích.

Quiz và câu hỏi gợi mở

Quiz

Mục đích chính của “out-of-bag” (OOB) error trong RF là gì?

  • Để ước tính độ chính xác của RF → Đúng
  • Để tính toán sai số huấn luyện của mô hình → Sai vì

Gợi mở

Thường thì model nào sẽ phù hợp nhất với Time series data? → RNN, LSTM

Biểu Đồ

Liên Kết Ngược