Gradient Descent

Bài note tham khảo trên trang: https://machinelearningcoban.com/2017/01/12/gradientdescent/

I. Introduction

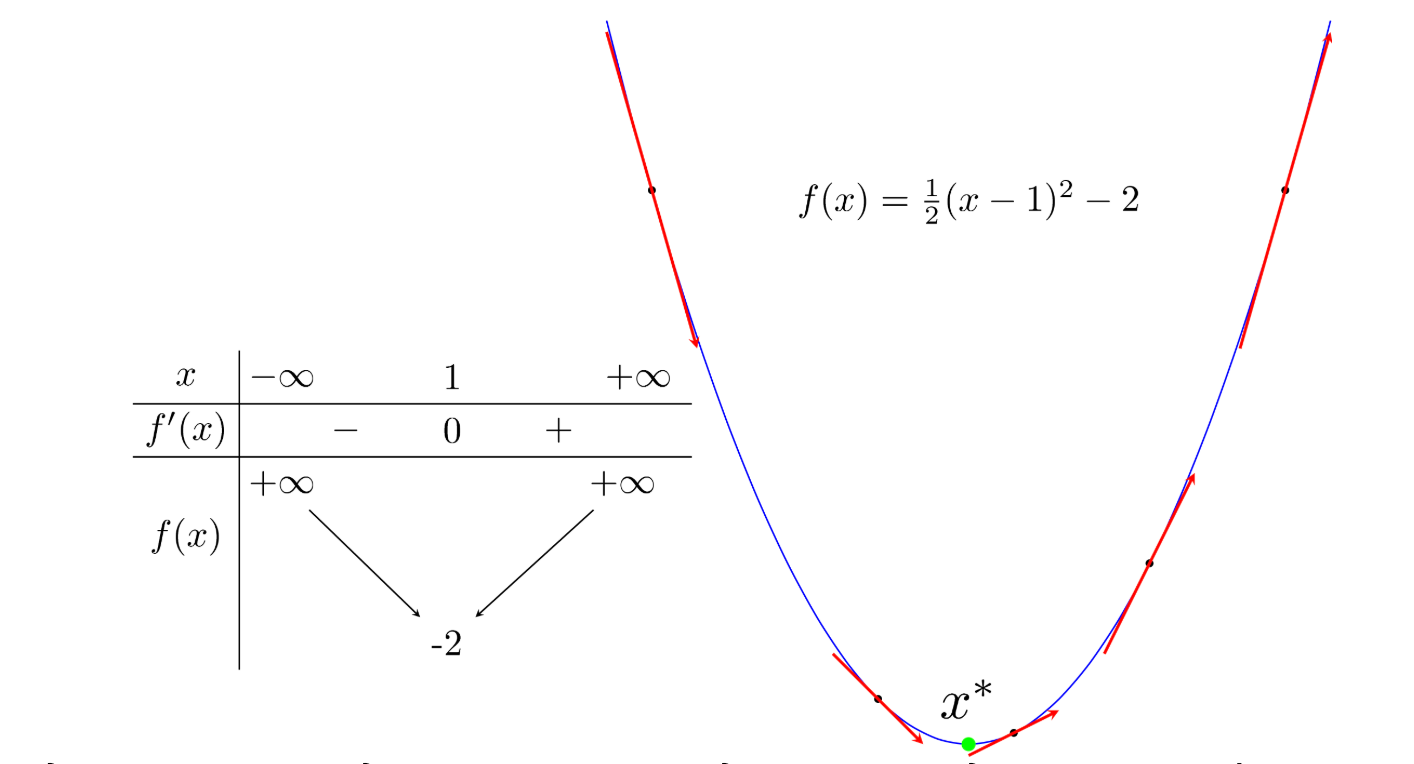
Điểm xanh lục là điểm local minimum (cực tiểu) và cũng là gobal minimum (điểm mà hàm số đạt giá trị nhỏ nhất). Giả sử ta quan tâm đến một hàm số một biến có đạo hàm ở mọi điểm y = f (x), ta có:

• Local minimum $x^{\ast }$ có đạo hàm bằng $f^{\prime }(x^{\ast })=0$
  • Trong lân cận, đạo hàm các điểm phía trái $x^{\ast }$: có giá trị dương
  • đạo hàm các điểm phía trái $x^{\ast }$: có giá trị âm
• Đường tiếp tuyến với đồ thị hàm số đó tại 1 điểm bất kỳ có hệ số góc chính bằng đạo hàm của hàm số tại điểm đó.

Gradient Descent

Trong Machine Learning nói riêng và Toán Tối Ưu nói chung, chúng ta thường xuyên phải tìm giá trị nhỏ nhất (hoặc đôi khi là lớn nhất) của một hàm số nào đó. Ví dụ như các hàm mất mát trong hai bài Linear regression và K-Mean. Nhìn chung, việc tìm global minimum của các hàm mất mát trong Machine Learning là rất phức tạp, thậm chí là bất khả thi. Thay vào đó, người ta thường cố gắng tìm các điểm local minimum, và ở một mức độ nào đó, coi đó là nghiệm cần tìm của bài toán.

Các điểm local minimum là nghiệm của phương trình đạo hàm bằng 0. Nếu bằng một cách nào đó có thể tìm được toàn bộ (hữu hạn) các điểm cực tiểu, ta chỉ cần thay từng điểm local minimum đó vào hàm số rồi tìm điểm làm cho hàm có giá trị nhỏ nhất. Tuy nhiên, trong hầu hết các trường hợp, việc giải phương trình đạo hàm bằng 0 là bất khả thi. Nguyên nhân có thể đến từ sự phức tạp của dạng của đạo hàm, từ việc các điểm dữ liệu có số chiều lớn, hoặc từ việc có quá nhiều điểm dữ liệu.

Hướng tiếp cận phổ biến nhất là xuất phát từ một điểm mà chúng ta coi là gần với nghiệm của bài toán, sau đó dùng một phép toán lặp để tiến dần đến điểm cần tìm, tức đến khi đạo hàm gần với 0. Gradient Descent (viết gọn là GD) và các biến thể của nó là một trong những phương pháp được dùng nhiều nhất.

II. Gradient Descent cho hàm 1 biến

Giả sử $x_t$ là điểm ta tìm được sau vòng lặp thứ $t$. Ta cần tìm một thuật toán để đưa $x_t$ về càng gần $x^{\ast }$ càng tốt. Ta thấy rằng:

• Nếu đạo hàm của hàm số tại $x_t:f^{\prime }(x_t)>0$ thì $x_t$ nằm về bên phải so với $x^{\ast }$ (và ngược lại). Để điểm tiếp theo $x_{t+1}$ gần với $x^{\ast }$ hơn, chúng ta cần di chuyển $x_t$ về phía bên trái, tức về phía âm. Nói các khác, chúng ta cần di chuyển ngược dấu với đạo hàm:

$$x_{t+1}=x_t+\Delta$$

Trong đó $\Delta$ là đại lượng ngược dấu với đạo hàm $f ^′(x_t)$
![[image-5.png]]

• $x_t$ càng xa $x^{\ast }$ về phía phải thì $f^{\prime }(x_t)$ càng lớn hơn với 0 (và ngược lại). Vậy lượng di chuyển $\Delta$, một cách trực quan nhất là tỉ lệ thuận với $-f^{\prime }(x_t)$.

Từ hai nhận xét trên ta có được công thức cập nhật:

$$x_{t+1}=x_t+\eta f^{\prime }(x_t)$$

Trong đó η (eta) là một số dương được gọi là learning rate (tốc độ học). Dấu trừ thể hiện việc chúng ta phải đi ngược với đạo hàm (Đây cũng chính là lý do phương pháp này được gọi là Gradient Descent - descent nghĩa là đi ngược). Các quan sát đơn giản phía trên, mặc dù không phải đúng cho tất cả các bài toán, là nền tảng cho rất nhiều phương pháp tối ưu nói chung và thuật toán Machine Learning nói riêng.

Điểm khởi tạo khác nhau

1. grad để tính đạo hàm
2. cost để tính giá trị của hàm số. Hàm này không sử dụng trong thuật toán nhưng thường được dùng để kiểm tra việc tính đạo hàm của đúng không hoặc để xem giá trị của hàm số có giảm theo mỗi vòng lặp hay không.
3. myGD1 là phần chính thực hiện thuật toán Gradient Desent nêu phía trên. Đầu vào của hàm số này là learning rate và điểm bắt đầu. Thuật toán dừng lại khi đạo hàm có độ lớn đủ nhỏ.

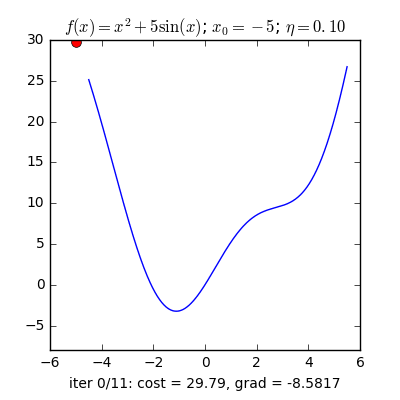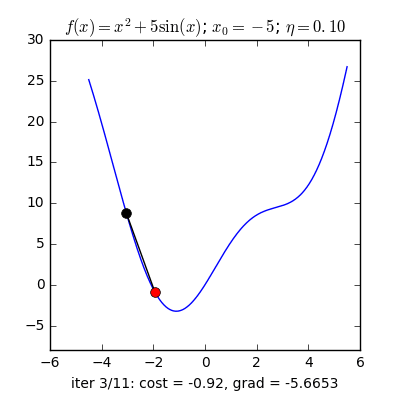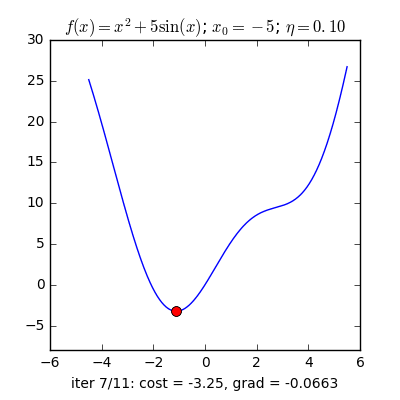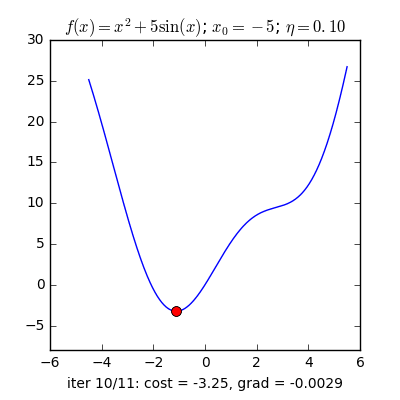
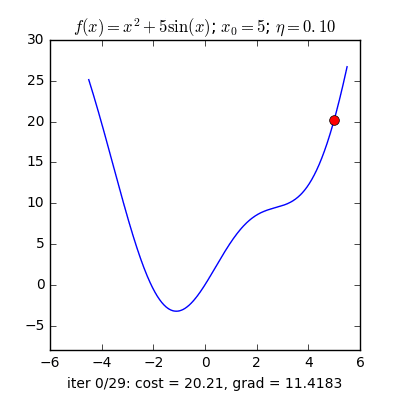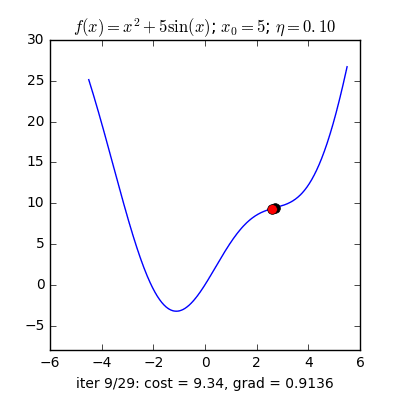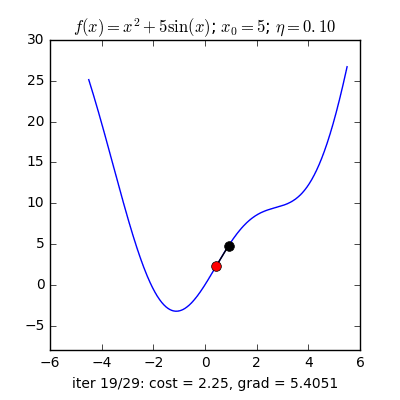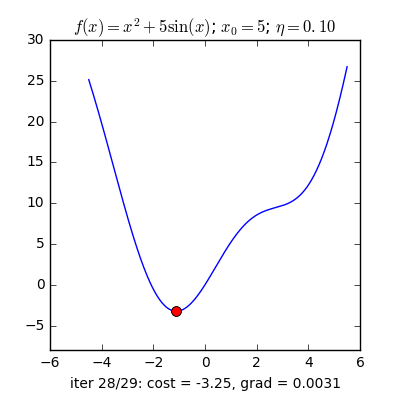
Với các điểm ban đầu khác nhau, thuật toán của chúng ta tìm được nghiệm gần giống nhau, mặc dù với tốc độ hội tụ khác nhau.

Learning rate khác nhau

Tốc độ hội tụ của GD không những phụ thuộc vào điểm khởi tạo ban đầu mà còn phụ thuộc vào learning rate.

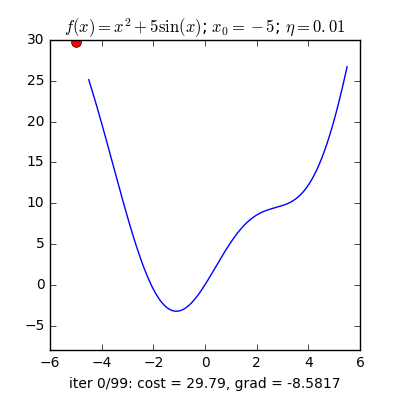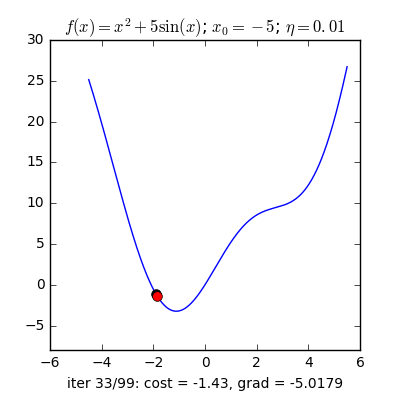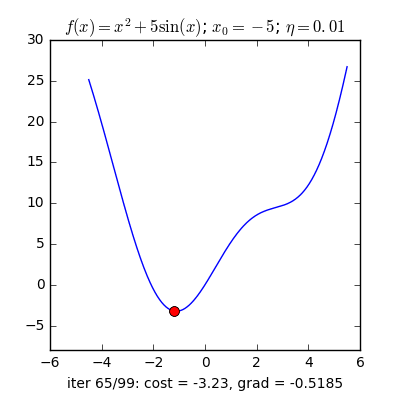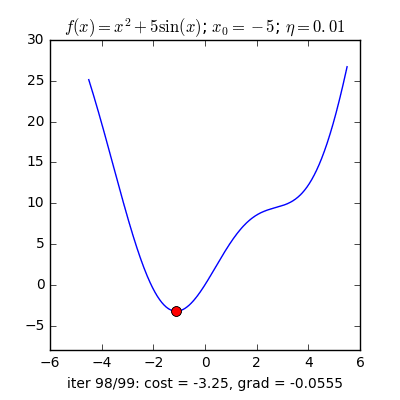
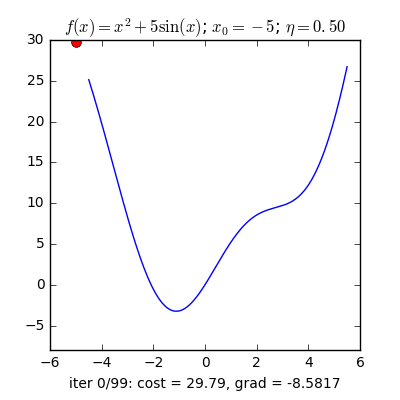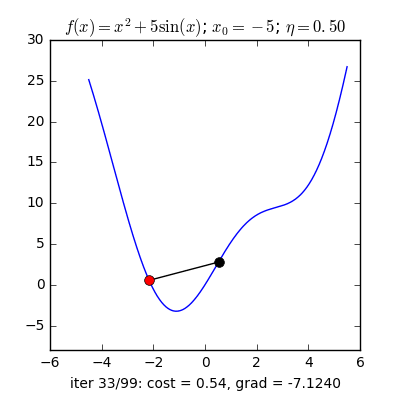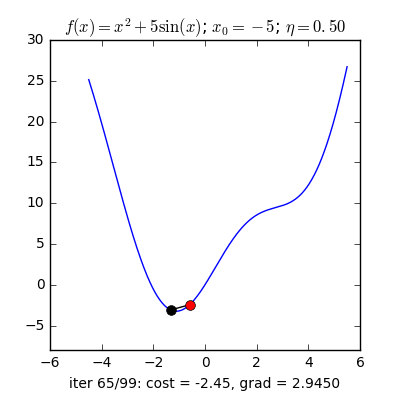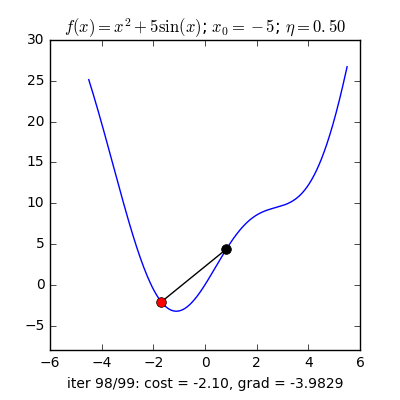
Với cùng điểm khởi tạo $x_0=-5$ nhưng learning rate khác nhau, ta quan sát thấy hai điều:

• Với learning rate nhỏ η=0.01, tốc độ hội tụ rất chậm. Trong thực tế, khi việc tính toán trở nên phức tạp, learning rate quá thấp sẽ ảnh hưởng tới tốc độ của thuật toán rất nhiều, thậm chí không bao giờ tới được đích.
• Với learning rate lớn η=0.5, thuật toán tiến rất nhanh tới gần đích sau vài vòng lặp. Tuy nhiên, thuật toán không hội tụ được vì bước nhảy quá lớn, khiến nó cứ quẩn quanh ở đích. Việc lựa chọn learning rate rất quan trọng trong các bài toán thực tế. Việc lựa chọn giá trị này phụ thuộc nhiều vào từng bài toán và phải làm một vài thí nghiệm để chọn ra giá trị tốt nhất. Ngoài ra, tùy vào một số bài toán, GD có thể làm việc hiệu quả hơn bằng cách chọn ra learning rate phù hợp hoặc chọn learning rate khác nhau ở mỗi vòng lặp.

III. Gradient Descent cho hàm nhiều biến

Giả sử ta cần tìm global minimum cho hàm $f(\theta )$ trong đó $\theta$ (theta) là một vector, thường được dùng để ký hiệu tập hợp các tham số của một mô hình cần tối ưu (trong Linear Regression thì các tham số chính là hệ số w). Đạo hàm của hàm số đó tại một điểm θ bất kỳ được ký hiệu là ∇θf(θ) (hình tam giác ngược đọc là nabla). Tương tự như hàm 1 biến, thuật toán GD cho hàm nhiều biến cũng bắt đầu bằng một điểm dự đoán ${\theta }_0$, sau đó, ở vòng lặp thứ t, quy tắc cập nhật là:

$${\theta }_{t+1}={\theta }_t-\eta {\nabla }_{\theta }f({\theta }_t)$$

Quy tắc cần nhớ: luôn luôn đi ngược hướng với đạo hàm.

Việc tính toán đạo hàm của các hàm nhiều biến là một kỹ năng cần thiết. Đọc lại bài 2. Giải tích ma trận

Trong bài toán Linear Regression

Áp dụng Gradient Descent để tối ưu hàm mất mát của Linear Regression bằng thuật toán GD. Ta có hàm mất mát của Linear Regression là:

$$\mathcal{L}(\mathbf{w})=\frac{1}{2N}||\mathbf{y}-\bar{\mathbf{X}}\mathbf{w}|{|}_2^2$$

Chú ý: hàm này có khác một chút so với hàm trong bài Linear Regression. Mẫu số có thêm N là số lượng dữ liệu trong training set. Việc lấy trung bình cộng của lỗi này nhằm giúp tránh trường hợp hàm mất mát và đạo hàm có giá trị là một số rất lớn, ảnh hưởng tới độ chính xác của các phép toán khi thực hiện trên máy tính. Về mặt toán học, nghiệm của hai bài toán là như nhau.

Đạo hàm của hàm mất mát là:

undefined