Nội dung bài sẽ được chia thành hai phần chính, Phần đầu tiên bao gồm mục 1, 2, 3, 4, 5 bàn luận về các vấn đề trong việc lấy mẫu để ước lượng các Đại lượng thống kê và Phương pháp ước lượng tổng thể bằng kỹ thuật Bootstrap. Phần thứ hai sẽ bàn luận về các Phân phối xác suất.

Nội dung được soạn với giả định rằng các bạn đã được học Thống kê ứng dụng và không đi lại những công thức đã học mà sẽ thảo luận về các vấn đề liên quan trong lĩnh vực DS, Kinh tế lượng, ML, …

Mở đầu: Dữ liệu và Phân phối mẫu

Trong các buổi trước chúng ta đã biết đến khái niệm lấy mẫu và tổng thể, và biết rằng việc lấy mẫu để giải quyết cho vấn đề thiếu điều kiện trong việc thu thập dữ liệu rất lớn trong tổng thể. Nhưng đó là về mặt quá khứ, cách đây nhiều năm. Trong thời đại BigData và các thuật toán ML, AI phát triển như hiện nay, các bạn nghĩ thử xem việc lấy Mẫu để ước lượng, xấp xỉ cho tổng thể liệu còn quan trọng và cần thiết không? (Câu hỏi để mọi người thảo luận, dẫn nhập)

Tuy nhiên thực tế, sự bùng nổ của dữ liệu từ khác nhau về chất lượng và mức độ liên quan thì lại càng củng cố vai trò của lấy mẫu hơn. Việc lấy mẫu sẽ như một công cụ giúp làm việc hiệu quả với nhiều loại dữ liệu và giảm thiểu sai lệch (bias).

Ví dụ về xử lý hiệu quả: Ta thử tính mean của tổng thể là 100.000.000 mẫu với việc lấy mẫu rồi tính Mean ước lượng tổng thể. Rõ ràng là việc nguồn lực để tính toán toàn bộ tổng thể sẽ tiêu tốn hơn và việc đó có thể cải thiện rất nhiều bằng cách chỉ cần Hi sinh một ít sai số (error).

Trong các dự án big data, các mô hình dự báo thường được phát triển và thử nghiệm trên các mẫu dữ liệu nhỏ sau đó mới triển khai lên toàn bộ Database. Ngoài ra, lấy mẫu cũng được sử dụng trong nhiều loại kiểm định khác nhau (ví dụ, so sánh tác động của các thiết kế trang web đối với số lượt nhấp).

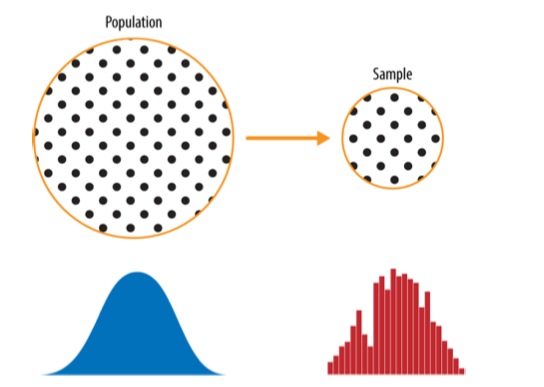
1. Lấy mẫu ngẫu nhiên và Sai lệch mẫu

Một mẫu (sample) là một tập con của dữ liệu được lấy ra từ một tập dữ liệu lớn hơn; trong thống kê, tập dữ liệu lớn hơn này được gọi là tổng thể (population). Khái niệm tổng thể là một tập dữ liệu lớn, được xác định rõ ràng (nhưng đôi khi mang tính lý thuyết hoặc giả định).

Lấy mẫu ngẫu nhiên (random sampling) là một quá trình trong đó mỗi phần tử có sẵn trong tổng thể đều có cơ hội như nhau để được chọn vào mẫu ở mỗi lần rút. Mẫu thu được theo cách này được gọi là mẫu ngẫu nhiên đơn giản (simple random sample).

Việc lấy mẫu có thể được thực hiện có hoàn lại (with replacement), nghĩa là các quan sát sau khi được chọn sẽ được đưa trở lại tổng thể để có thể được chọn lại trong những lần rút tiếp theo. Hoặc có thể được thực hiện không hoàn lại (without replacement), khi đó các quan sát sau khi đã được chọn sẽ không còn khả năng xuất hiện trong các lần rút tiếp theo. Các khái niệm này sẽ được bàn luận kĩ hơn ở phần sau.

Trước khi xây dựng một ước lượng hoặc mô hình dựa trên mẫu, chất lượng dữ liệu thường quan trọng hơn số lượng dữ liệu. Trong khoa học dữ liệu, chất lượng dữ liệu bao gồm mức độ đầy đủ, tính nhất quán của định dạng, độ sạch, và độ chính xác của từng điểm dữ liệu. Thống kê bổ sung thêm một khái niệm quan trọng: tính đại diện (representativeness).

Một ví dụ kinh điển là cuộc thăm dò của tạp chí Literary Digest năm 1936, trong đó dự đoán ứng cử viên Alf Landon sẽ chiến thắng Franklin Roosevelt. Literary Digest, một tạp chí hàng đầu thời bấy giờ, đã khảo sát toàn bộ danh sách người đăng ký của mình cùng với các danh sách bổ sung khác, tổng cộng hơn 10 triệu người, và dự đoán Landon sẽ thắng áp đảo. Trong khi đó, George Gallup, người sáng lập Gallup Poll, chỉ thực hiện các cuộc khảo sát hai tuần một lần với khoảng 2.000 người nhưng lại dự đoán chính xác chiến thắng của Roosevelt. Sự khác biệt nằm ở cách lựa chọn đối tượng được khảo sát.

Literary Digest ưu tiên số lượng, nhưng lại ít chú trọng đến phương pháp chọn mẫu. Kết quả là họ đã khảo sát chủ yếu những người có địa vị kinh tế – xã hội tương đối cao (người đăng ký tạp chí của họ, cùng với những người xuất hiện trong các danh sách tiếp thị do sở hữu những tài sản xa xỉ như điện thoại và ô tô). Điều này dẫn đến sai lệch mẫu; tức là mẫu thu được khác với tổng thể mà nó được dùng để đại diện theo một cách có ý nghĩa và không ngẫu nhiên.

Thuật ngữ không ngẫu nhiên ở đây rất quan trọng—hầu như không có mẫu nào, kể cả mẫu ngẫu nhiên, đại diện hoàn hảo cho tổng thể. Sai lệch mẫu xảy ra khi sự khác biệt đó là đáng kể và có xu hướng tiếp tục xuất hiện ở các mẫu khác được lấy theo cùng một cách như mẫu ban đầu.

Bàn luận thêm: Sai lệch lấy mẫu tự chọn (Self-Selection Sampling Bias)

Các bài đánh giá về nhà hàng, khách sạn, quán cà phê, hoặc sản phẩm trên sàn thương mại điện tử ví dụ như shoppe rất dễ bị sai lệch, bởi vì những người gửi đánh giá không được lựa chọn một cách ngẫu nhiên; thay vào đó, chính họ tự chủ động viết đánh giá. Điều này dẫn đến sai lệch do tự chọn: những người có viết đánh giá sẽ thường là nhóm có thể đã có trải nghiệm không tốt, có mối liên hệ nào đó với cơ sở được đánh giá, hoặc đơn giản là họ thuộc một nhóm người khác với những người không viết đánh giá (cái này thì rõ ràng chúng ta sẽ không biết được).

Cần lưu ý rằng, mặc dù các mẫu tự chọn có thể không đáng tin cậy khi dùng để phản ánh chính xác tình trạng thực tế, chúng vẫn có thể tin cậy khi dùng để so sánh với những cách lấy mẫu khác trong việc đánh giá tính khách quan của lấy mẫu.

Sai lệch (Bias)

Từ đó chúng ta sẽ đến với khái niệm Bias. Trong thống kê, sai lệch (bias) hay thiên kiến, thiên vị → đề cập đến các sai số trong đo lường hoặc do lấy mẫu và điểm quan trọng là nó phải mang tính hệ thống (Khác với Error là biến ngẫu nhiên), Rõ ràng là sẽ xuất hiện trong chính quá trình đo lường hoặc lấy mẫu. Cần phân biệt rõ giữa sai số do ngẫu nhiên và sai số do sai lệch.

Hãy xem xét ví dụ sau: Kết quả một khẩu súng bắn vào bia. Viên đạn sẽ không trúng chính xác tâm bia trong mọi lần bắn, thậm chí phần lớn thời gian cũng không trúng. Một quá trình không bị sai lệch (unbiased) vẫn tạo ra sai số, nhưng sai số đó là ngẫu nhiên và không có xu hướng lệch mạnh về một hướng nào (xem Hình).

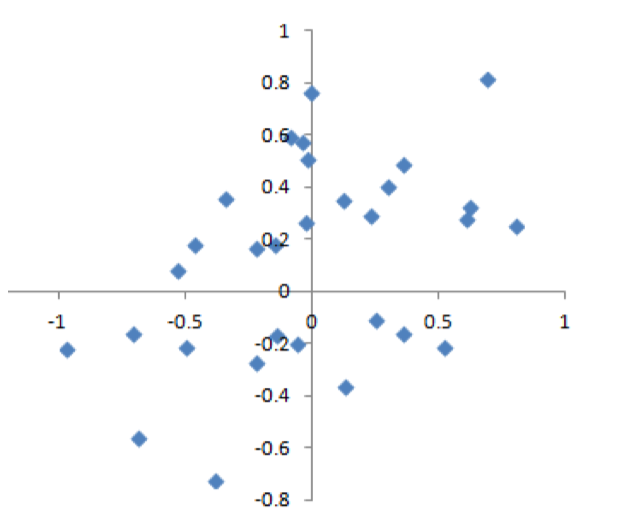
Ngược lại, các kết quả minh họa trong Hình dưới cho thấy một quá trình bị sai lệch—vẫn tồn tại sai số ngẫu nhiên, nhưng đồng thời có thêm một sai lệch có hệ thống: các phát bắn có xu hướng rơi vào góc trên bên phải.

Sai lệch có thể tồn tại dưới nhiều hình thức khác nhau và có thể dễ nhận ra hoặc rất khó để nhận ra. Khi kết quả cho thấy dấu hiệu của Bias (sai lệch) (ví dụ, khi so sánh với một mốc chuẩn hoặc với giá trị thực tế), điều đó thường là một chỉ báo rằng mô hình thống kê hoặc mô hình học máy đã được đặc tả sai, hoặc rằng một biến quan trọng nào đó đã bị bỏ sót.

Lựa chọn ngẫu nhiên (Random Selection)

Để tránh vấn đề sai lệch mẫu đã khiến Literary Digest dự đoán Landon chiến thắng Roosevelt, George Gallup đã lựa chọn các phương pháp lấy mẫu mang tính khoa học hơn nhằm tạo ra một mẫu đại diện cho cử tri Hoa Kỳ. Ngày nay, có nhiều phương pháp khác nhau để đạt được tính đại diện, nhưng cốt lõi của tất cả các phương pháp đó vẫn là lấy mẫu ngẫu nhiên. (Sẽ tìm ví dụ khác sát với bối cảnh hơn)

Tuy nhiên, lấy mẫu ngẫu nhiên không phải lúc nào cũng dễ thực hiện. Việc xác định đúng tổng thể có thể tiếp cận được (accessible population) là yếu tố then chốt. Giả sử chúng ta muốn xây dựng một hồ sơ đại diện cho khách hàng và cần tiến hành một cuộc khảo sát thử nghiệm (pilot survey). Cuộc khảo sát này cần đảm bảo tính đại diện và chắc chắn rằng nó sẽ đòi hỏi nhiều công sức bỏ ra để nghiên cứu kĩ chiến lược khảo sát sao cho khách quan nhất có thể.

Trước hết, chúng ta phải xác định thế nào là một khách hàng. Chẳng hạn, ta có thể chọn tất cả các bản ghi khách hàng có giá trị mua hàng lớn hơn 0. Nhưng liệu có nên bao gồm tất cả khách hàng trong quá khứ không? Có tính các giao dịch hoàn tiền không? Các giao dịch kiểm thử nội bộ thì sao? Còn các đại lý bán lại? Có tính cả bên đại diện thanh toán lẫn khách hàng cuối hay không?

Tiếp theo, cần xác định quy trình lấy mẫu. Quy trình này có thể đơn giản là “chọn ngẫu nhiên 100 khách hàng.” Trong những trường hợp lấy mẫu từ một dòng dữ liệu liên tục (ví dụ, giao dịch khách hàng theo thời gian thực hoặc khách truy cập website), yếu tố thời điểm có thể rất quan trọng (chẳng hạn, một người truy cập web lúc 10 giờ sáng ngày thường có thể khác với một người truy cập lúc 10 giờ tối vào cuối tuần).

Khái niệm lấy mẫu phân tầng (stratified sampling) có thể sẽ giải quyết được vấn đề này, tổng thể được chia thành các tầng (strata), và các mẫu ngẫu nhiên được lấy từ mỗi tầng. Ví dụ 1: Các nhà thăm dò chính trị có thể muốn tìm hiểu khuynh hướng bầu cử của các nhóm người da trắng, da đen và người gốc Tây Ban Nha. Nếu chỉ lấy một mẫu ngẫu nhiên đơn giản từ toàn bộ tổng thể, số lượng người da đen và người gốc Tây Ban Nha trong mẫu sẽ quá ít; do đó, trong lấy mẫu phân tầng, các tầng này có thể được tăng trọng số để thu được kích thước mẫu tương đương giữa các nhóm.

Ví dụ 2: Xét một bài toán phân loại trong y học: dự đoán bệnh nhân có mắc ung thư hay không dựa trên dữ liệu lâm sàng. Trong thực tế, số lượng bệnh nhân không mắc ung thư thường lớn hơn rất nhiều so với số bệnh nhân mắc ung thư. Đây là một bài toán có mất cân bằng lớp (class imbalance) nghiêm trọng.

Nếu ta lấy mẫu ngẫu nhiên đơn giản từ dữ liệu thực tế:

Mẫu thu được sẽ chứa rất nhiều bệnh nhân khỏe mạnh.
Số lượng bệnh nhân ung thư trong mẫu sẽ rất ít.

Hệ quả là mô hình học máy có thể:

Học cách luôn dự đoán “không ung thư” và vẫn đạt độ chính xác (accuracy) cao.
Nhưng lại thất bại trong việc phát hiện bệnh ung thư, vốn là lớp quan trọng nhất.

Một cách tiếp cận phổ biến là áp dụng tư duy lấy mẫu phân tầng, trong đó hai tầng là:

Bệnh nhân mắc ung thư.
Bệnh nhân không mắc ung thư.

Ta có thể cố tình lấy mẫu sao cho hai tầng có kích thước gần bằng nhau, nhằm:

Buộc mô hình học được đặc trưng của lớp hiếm (ung thư).
Giảm thiên lệch về phía lớp chiếm đa số.

Tuy nhiên, điều này dẫn đến một tranh luận quan trọng trong thống kê và khoa học dữ liệu. Một số ý kiến cho rằng việc “cân bằng hóa dữ liệu” như vậy:

Làm mất đi tính thực tế của phân bố xác suất, vì trong đời sống thực, ung thư đúng là hiếm.
Khi triển khai mô hình ra thực tế, mô hình có thể đánh giá sai xác suất tuyệt đối (ví dụ: dự đoán nguy cơ ung thư cao hơn thực tế).

Do đó, trong thực hành, cách tiếp cận thường là:

Huấn luyện mô hình trên dữ liệu đã được cân bằng hoặc phân tầng để học tốt đặc trưng của lớp hiếm.
Đánh giá và hiệu chỉnh kết quả trên phân bố thực tế, hoặc sử dụng các thước đo phù hợp hơn accuracy (như recall, precision, ROC-AUC).

Ví dụ này cho thấy lấy mẫu phân tầng không chỉ là một kỹ thuật thống kê, mà còn liên quan trực tiếp đến mục tiêu phân tích, đạo đức mô hình, và cách diễn giải kết quả trong bối cảnh thực tế.

Quy mô so với Chất lượng: Khi nào quy mô thực sự quan trọng?

Trong kỷ nguyên dữ liệu lớn (big data), thật bất ngờ khi khẳng định rằng nhỏ lại tốt hơn. Thời gian và công sức dành cho lấy mẫu ngẫu nhiên không chỉ giúp giảm sai lệch mà còn cho phép tập trung nhiều hơn vào khám phá dữ liệu và chất lượng dữ liệu. Ví dụ, dữ liệu bị thiếu và các điểm ngoại lai (outliers) có thể chứa thông tin hữu ích. Việc truy vết các giá trị thiếu hoặc đánh giá các outlier trong hàng triệu bản ghi có thể là điều không khả thi về chi phí, nhưng làm điều đó trên một mẫu vài nghìn bản ghi thì hoàn toàn khả thi. Việc vẽ đồ thị dữ liệu và kiểm tra thủ công cũng trở nên nặng nề nếu dữ liệu quá nhiều.

Vậy khi nào cần đến khối lượng dữ liệu khổng lồ?

Giá trị thật sự của big data là khi dữ liệu không chỉ lớn mà còn thưa (sparse). Hãy xem xét các truy vấn tìm kiếm mà Google nhận được, trong đó:

các cột là từ khóa,
các hàng là từng truy vấn tìm kiếm,
giá trị ô là 0 hoặc 1, tùy theo truy vấn có chứa từ khóa đó hay không.

Mục tiêu là xác định điểm đến tìm kiếm được dự đoán tốt nhất cho một truy vấn nhất định. Tiếng Anh có hơn 150.000 từ, và Google xử lý hơn một nghìn tỷ truy vấn mỗi năm. Điều này tạo ra một ma trận khổng lồ, trong đó phần lớn các ô đều là “0.”

Đây là một bài toán big data đúng nghĩa—chỉ khi tích lũy được lượng dữ liệu khổng lồ như vậy thì mới có thể trả về kết quả tìm kiếm hiệu quả cho hầu hết các truy vấn. Và càng tích lũy nhiều dữ liệu, kết quả càng tốt. Với các từ khóa phổ biến, đây không phải là vấn đề lớn—dữ liệu hữu ích có thể được thu thập khá nhanh cho một số ít chủ đề cực kỳ phổ biến tại một thời điểm nhất định. Giá trị thực sự của công nghệ tìm kiếm hiện đại nằm ở khả năng trả về các kết quả chi tiết và hữu ích cho một phạm vi rất rộng các truy vấn, bao gồm cả những truy vấn xuất hiện với tần suất cực thấp, chẳng hạn chỉ một lần trong một triệu.

Hãy xem xét cụm tìm kiếm “Ricky Ricardo and Little Red Riding Hood.” Trong những ngày đầu của internet, truy vấn này có lẽ sẽ trả về các kết quả về Ricky Ricardo (ban nhạc trưởng), chương trình truyền hình I Love Lucy—nơi nhân vật này xuất hiện—và câu chuyện thiếu nhi Little Red Riding Hood. Mỗi mục riêng lẻ đều có rất nhiều lượt tìm kiếm để tham chiếu, nhưng sự kết hợp của chúng thì lại rất hiếm. Về sau, khi hàng nghìn tỷ truy vấn đã được tích lũy, truy vấn này trả về chính xác tập I Love Lucy trong đó Ricky kể lại, theo cách kịch tính, câu chuyện Little Red Riding Hood cho con trai sơ sinh của mình, trong một sự pha trộn hài hước giữa tiếng Anh và tiếng Tây Ban Nha.

Ví dụ khác: Khi tìm kiếm “quán cà phê yên tĩnh học bài gần UEH + mở tới 11 h”

Dữ liệu ít: trả về các list quán cà phê chung chung
Dữ liệu đủ lớn: trả về đúng nhóm kết quả “học bài”, “ổ cắm”, “ít ồn”, “mở khuya”, “gần khu vực X”

Thông điệp: Đây là truy vấn “nhiều điều kiện”, mỗi điều kiện riêng lẻ phổ biến nhưng kết hợp thì hiếm.

Cần lưu ý rằng số lượng bản ghi thực sự liên quan—những bản ghi trong đó truy vấn này, hoặc một truy vấn rất tương tự, xuất hiện (kèm theo thông tin về liên kết mà người dùng cuối cùng đã nhấp)—chỉ cần ở mức vài nghìn là có thể đủ hiệu quả. Tuy nhiên, để thu được những bản ghi liên quan đó, cần đến hàng nghìn tỷ điểm dữ liệu (và dĩ nhiên, lấy mẫu ngẫu nhiên sẽ không giúp ích trong trường hợp này).

Sample Mean Versus Population Mean (Trung bình mẫu và trung bình tổng thể)

Ký hiệu x̄ (đọc là “x-bar”) được dùng để biểu diễn giá trị trung bình của một mẫu được rút ra từ một tổng thể, trong khi μ được dùng để biểu diễn giá trị trung bình của toàn bộ tổng thể. Tại sao cần phải phân biệt hai khái niệm này?

Lý do là vì thông tin về mẫu thì có thể quan sát trực tiếp, còn thông tin về các tổng thể lớn thì thường được suy luận gián tiếp thông qua các mẫu nhỏ hơn. Các nhà thống kê học có xu hướng tách bạch rõ ràng hai khái niệm này trong hệ thống ký hiệu, nhằm tránh nhầm lẫn giữa cái được quan sát và cái được suy luận.

Tổng hợp ý chỉnh của mục đầu tiên

Ngay cả trong kỷ nguyên dữ liệu lớn (big data), lấy mẫu ngẫu nhiên vẫn là một công cụ quan trọng trong “kho vũ khí” của nhà khoa học dữ liệu.
Sai lệch (bias) xảy ra khi các phép đo hoặc quan sát bị sai một cách có hệ thống, do không đại diện đúng cho toàn bộ tổng thể.
Chất lượng dữ liệu thường quan trọng hơn số lượng dữ liệu; và lấy mẫu ngẫu nhiên có thể giảm sai lệch cũng như tạo điều kiện cải thiện chất lượng dữ liệu, điều mà nếu làm trực tiếp trên toàn bộ dữ liệu có thể sẽ tốn kém hoặc không khả thi.

2. Selection Bias (Sai lệch chọn mẫu / sai lệch lựa chọn)

Để diễn giải lại câu nói của Yogi Berra: nếu bạn không biết mình đang tìm cái gì, chỉ cần tìm đủ kỹ thì bạn sẽ tìm thấy nó.

Selection bias (sai lệch lựa chọn) đề cập đến việc chọn dữ liệu một cách có chủ ý hoặc vô thức theo cách dẫn đến những kết luận gây hiểu nhầm hoặc chỉ có giá trị nhất thời.

Thuật ngữ chính về Selection Bias

Selection bias: Sai lệch phát sinh từ cách các quan sát được lựa chọn.
Data snooping: Việc lục lọi dữ liệu quá mức để tìm ra một điều gì đó “thú vị”.
Vast search effect: Sai lệch hoặc kết quả không thể tái lập, phát sinh từ việc chạy lặp đi lặp lại nhiều mô hình, hoặc xây dựng mô hình với rất nhiều biến dự báo.

Nếu bạn xác định trước một giả thuyết và tiến hành một thí nghiệm được thiết kế tốt để kiểm định giả thuyết đó, bạn có thể đặt niềm tin cao vào kết luận thu được. Tuy nhiên, trên thực tế, điều này không phải lúc nào cũng xảy ra. Thường thì người ta nhìn vào dữ liệu sẵn có và cố gắng tìm ra các khuôn mẫu. Nhưng câu hỏi đặt ra là: những khuôn mẫu đó có thật không? Hay chúng chỉ là sản phẩm của data snooping—tức là việc tìm kiếm dữ liệu một cách quá mức cho đến khi xuất hiện một điều gì đó trông có vẻ thú vị?

Trong giới thống kê có một câu nói nổi tiếng:

“Nếu bạn tra tấn dữ liệu đủ lâu, sớm hay muộn nó cũng sẽ thú nhận.”

Sự khác biệt giữa một hiện tượng được xác nhận thông qua kiểm định giả thuyết bằng thí nghiệm, và một hiện tượng được “phát hiện” bằng cách dò xét dữ liệu sẵn có, có thể được minh họa bằng thí nghiệm tư duy sau.

Hãy tưởng tượng có người nói rằng họ có thể tung một đồng xu và khiến nó ra mặt ngửa liên tiếp trong 10 lần. Bạn thách thức họ (tương đương với một thí nghiệm), và họ thực sự tung 10 lần, tất cả đều ra ngửa. Rõ ràng, bạn sẽ cho rằng người này có năng lực đặc biệt, bởi vì xác suất để 10 lần tung đều ra ngửa chỉ là 1 trên 1.000 nếu hoàn toàn ngẫu nhiên.

Bây giờ, hãy tưởng tượng một người dẫn chương trình tại một sân vận động yêu cầu 20.000 khán giả, mỗi người tung đồng xu 10 lần, và báo lại nếu họ có 10 lần ngửa liên tiếp. Xác suất để ít nhất một người trong sân vận động đạt được điều này là cực kỳ cao (trên 99%—bằng 1 trừ đi xác suất không ai đạt được 10 lần ngửa). Rõ ràng, việc chọn ra sau khi đã quan sát người (hoặc những người) tung được 10 lần ngửa không cho thấy họ có tài năng đặc biệt—đó rất có thể chỉ là may mắn.

Vì việc xem xét lặp đi lặp lại các tập dữ liệu lớn là một giá trị cốt lõi của khoa học dữ liệu, nên selection bias là một vấn đề cần đặc biệt lưu tâm. Một dạng selection bias đặc biệt đáng lo ngại đối với data scientist là cái mà John Elder (người sáng lập Elder Research, một công ty tư vấn khai phá dữ liệu uy tín) gọi là vast search effect. Nếu bạn liên tục chạy các mô hình khác nhau và đặt ra nhiều câu hỏi khác nhau với một tập dữ liệu lớn, gần như chắc chắn bạn sẽ tìm thấy một điều gì đó “thú vị”. Nhưng liệu kết quả đó thực sự có ý nghĩa, hay chỉ là một ngoại lệ ngẫu nhiên?

Chúng ta có thể giảm thiểu rủi ro này bằng cách sử dụng tập dữ liệu giữ lại (holdout set)—và đôi khi là nhiều holdout set—để kiểm tra và xác thực hiệu năng. Elder cũng đề xuất sử dụng kỹ thuật mà ông gọi là target shuffling (về bản chất là một kiểm định hoán vị – permutation test) nhằm kiểm tra tính hợp lệ của các mối liên hệ dự báo mà mô hình khai phá dữ liệu gợi ý.

Các dạng selection bias điển hình khác trong thống kê, ngoài vast search effect, bao gồm: lấy mẫu không ngẫu nhiên, cherry-picking dữ liệu, lựa chọn khoảng thời gian sao cho làm nổi bật một hiệu ứng thống kê nào đó, và dừng thí nghiệm khi kết quả trông có vẻ “thú vị”.

Regression to the Mean (Hiện tượng hồi quy về trung bình)

Regression to the mean (hồi quy về trung bình) là một hiện tượng xảy ra khi ta quan sát các phép đo liên tiếp của cùng một biến: những quan sát cực đoan (rất cao hoặc rất thấp) thường sẽ được theo sau bởi các giá trị gần với trung bình hơn. Việc gán cho các giá trị cực đoan này những ý nghĩa hoặc tầm quan trọng đặc biệt rất dễ dẫn đến một dạng sai lệch lựa chọn (selection bias).

Những người hâm mộ thể thao hẳn đã quen thuộc với hiện tượng “Điểm rơi phong độ của cầu thủ” (Cầu thủ có thể xuất sắc nhất năm nhưng lại sa sút ở mùa kế tiếp). Trong số các vận động viên bắt đầu sự nghiệp của mình trong cùng một mùa giải (lớp tân binh), luôn có một người thi đấu vượt trội hơn tất cả những người còn lại. Tuy nhiên, thông thường, “tân binh của năm” này lại không duy trì được phong độ đó ở năm thứ hai. Vì sao lại như vậy?

Trong hầu hết các môn thể thao lớn, hiệu suất thi đấu tổng thể thường chịu ảnh hưởng của hai yếu tố:

Kỹ năng (skill)
May mắn (luck)

Hiện tượng hồi quy về trung bình là hệ quả của một dạng selection bias cụ thể. Khi ta chọn ra tân binh có thành tích tốt nhất, kết quả đó thường là sự kết hợp của kỹ năng tốt và may mắn nhất thời. Sang mùa giải tiếp theo, kỹ năng vẫn còn, nhưng yếu tố may mắn rất thường không lặp lại, dẫn đến việc thành tích giảm xuống—tức là “hồi quy” về mức trung bình.

Hiện tượng này lần đầu tiên được nhận diện bởi Francis Galton vào năm 1886 [Galton-1886], khi ông nghiên cứu các khuynh hướng di truyền. Chẳng hạn, con cái của những người cực kỳ cao có xu hướng không cao bằng cha mẹ của mình.

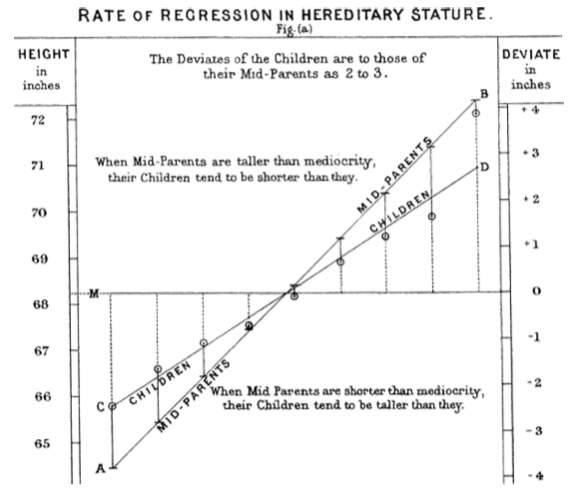
Cần phân biệt rõ regression to the mean (hồi quy về trung bình, mang nghĩa “quay trở lại”) với linear regression (hồi quy tuyến tính), là một phương pháp mô hình hóa thống kê nhằm ước lượng mối quan hệ tuyến tính giữa các biến dự báo và biến kết quả.

Ý chính của mục hai

Việc xác định giả thuyết trước, sau đó thu thập dữ liệu theo các nguyên tắc ngẫu nhiên hóa và lấy mẫu ngẫu nhiên, giúp giảm thiểu nguy cơ sai lệch, đảm bảo khách quan trong quy trình nghiên cứu.
Mọi hình thức phân tích dữ liệu khác đều tiềm ẩn rủi ro sai lệch phát sinh từ quá trình thu thập hoặc phân tích dữ liệu, chẳng hạn như chạy mô hình lặp đi lặp lại trong khai phá dữ liệu, data snooping trong nghiên cứu, hoặc lựa chọn các sự kiện “thú vị” sau khi đã quan sát kết quả.

3. Phân phối lấy mẫu của một thống kê (Sampling Distribution of a Statistic)

Thuật ngữ phân phối mẫu của một thống kê dùng để chỉ phân phối của một đại lượng thống kê mẫu khi ta rút nhiều mẫu khác nhau từ cùng một tổng thể. Phần lớn thống kê cổ điển tập trung vào việc suy luận từ các mẫu (nhỏ) sang các tổng thể (rất lớn).

Các thuật ngữ chính về phân phối lấy mẫu

Sample statistic (Thống kê mẫu):
Một đại lượng được tính toán trên một mẫu dữ liệu lấy từ một tổng thể lớn hơn.
Data distribution (Phân phối dữ liệu):
Phân phối tần suất của các giá trị dữ liệu riêng lẻ trong một tập dữ liệu.
Sampling distribution (Phân phối lấy mẫu):
Phân phối tần suất của một thống kê mẫu khi xét trên nhiều mẫu hoặc nhiều lần lấy mẫu lại.
Central limit theorem (Định lý giới hạn trung tâm):
Khuynh hướng mà phân phối lấy mẫu tiệm cận dạng chuẩn khi kích thước mẫu tăng lên.
Standard error (Sai số chuẩn):
Mức độ biến thiên (độ lệch chuẩn) của một thống kê mẫu qua nhiều mẫu
(không nhầm với độ lệch chuẩn – standard deviation – vốn đo độ biến thiên của các giá trị dữ liệu cá nhân).

Lưu ý phân biệt phân phối mẫu (sample distribution / data distribution) và phân phối lấy mẫu (sampling distribution)

Tiêu chí	Phân phối dữ liệu mẫu	Phân phối lấy mẫu
Phân phối của	Dữ liệu thô	Thống kê mẫu
Đơn vị	Quan sát cá nhân	Một con số tóm tắt (mean, var, …)
Số mẫu	1 mẫu	Rất nhiều mẫu (giả định / bootstrap)
Mục đích	Mô tả dữ liệu	Suy luận thống kê
Hình dạng	Có thể bất kỳ	Thường gần chuẩn
Liên quan đến	EDA	CI, SE, hypothesis test

Thông thường, một mẫu được rút ra với mục tiêu đo lường một đại lượng nào đó (thông qua một thống kê mẫu) hoặc xây dựng mô hình (thống kê hoặc học máy). Vì ước lượng hay mô hình của chúng ta dựa trên một mẫu, nên có thể tồn tại sai số; kết quả có thể khác nếu ta rút một mẫu khác. Do đó, điều chúng ta quan tâm là mức độ khác biệt có thể xảy ra—một mối quan tâm then chốt chính là độ biến thiên do lấy mẫu (sampling variability).

Nếu có rất nhiều dữ liệu, ta có thể rút thêm các mẫu và quan sát trực tiếp phân phối của thống kê mẫu. Tuy nhiên, trên thực tế, chúng ta thường tính toán ước lượng hoặc mô hình bằng toàn bộ dữ liệu sẵn có, nên việc rút thêm các mẫu độc lập từ tổng thể không dễ thực hiện.

Phân phối của một thống kê mẫu như trung bình thường đều đặn hơn và có dạng chuông hơn so với phân phối của chính dữ liệu gốc. Mẫu càng lớn, điều này càng rõ rệt. Đồng thời, kích thước mẫu càng lớn, thì phân phối của thống kê mẫu càng hẹp (độ biến thiên nhỏ hơn).

Điều này được minh họa qua một ví dụ sử dụng thu nhập hằng năm của các ứng viên vay vốn tại LendingClub. Ta lấy ba tập mẫu:

Một mẫu gồm 1.000 giá trị thu nhập riêng lẻ,
Một mẫu gồm 1.000 giá trị trung bình, mỗi trung bình được tính từ 5 quan sát,
Một mẫu gồm 1.000 giá trị trung bình, mỗi trung bình được tính từ 20 quan sát.

(Thêm code ở đây)

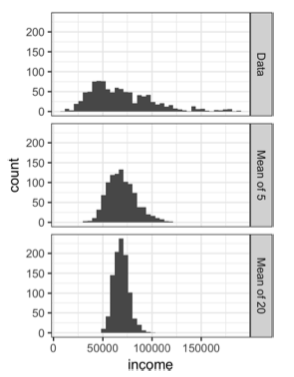
Histogram của các giá trị dữ liệu riêng lẻ có độ phân tán lớn và lệch phải, điều vốn dĩ thường thấy với dữ liệu thu nhập. Trong khi đó, histogram của trung bình của 5 và trung bình của 20 ngày càng tập trung hơn và có dạng chuông rõ rệt hơn.

Định lý Giới hạn Trung tâm

(Central Limit Theorem)

Hiện tượng các phân phối của đại lượng thống kê mẫu tiến gần đến phân phối chuẩn vừa được mô tả ở trên được gọi là định lý giới hạn trung tâm. Định lý này phát biểu rằng các giá trị trung bình được rút ra từ nhiều mẫu khác nhau sẽ có phân phối gần giống đường cong chuẩn hình chuông quen thuộc, ngay cả khi tổng thể gốc không tuân theo phân phối chuẩn, miễn là kích thước mẫu đủ lớn và mức độ lệch khỏi phân phối chuẩn của dữ liệu không quá nghiêm trọng.

Định lý giới hạn trung tâm cho phép sử dụng các công thức xấp xỉ chuẩn, chẳng hạn như phân phối t, trong việc tính toán phân phối lấy mẫu phục vụ cho suy luận thống kê—cụ thể là khoảng tin cậy và kiểm định giả thuyết.

Định lý này nhận được rất nhiều sự chú ý trong các giáo trình thống kê truyền thống vì nó là nền tảng cho toàn bộ “bộ máy” của kiểm định giả thuyết và khoảng tin cậy—những nội dung vốn chiếm tới một nửa dung lượng của các giáo trình đó. Các nhà khoa học dữ liệu cần phải hiểu được vai trò của nó; tuy nhiên, do kiểm định giả thuyết hình thức và khoảng tin cậy chỉ đóng vai trò tương đối nhỏ trong thực hành khoa học dữ liệu, và vì hiện tại người ta ưa chuộng bootstrap, nên định lý giới hạn trung tâm không còn “trung tâm” trong thực hành khoa học dữ liệu hiện đại.

Sai số chuẩn(Standard Error)

Sai số chuẩn (standard error) là một chỉ số đơn lẻ dùng để tóm tắt mức độ biến thiên trong phân phối lấy mẫu của một thống kê. Sai số chuẩn có thể được ước lượng bằng một công thức dựa trên độ lệch chuẩn mẫu s và kích thước mẫu n:

$Standard error = SE = \frac{s}{n}$

Khi kích thước mẫu tăng, sai số chuẩn giảm, phù hợp với những gì đã quan sát trong Hình thu nhập hằng năm của các ứng viên vay vốn tại LendingClub. Mối quan hệ giữa sai số chuẩn và kích thước mẫu đôi khi được gọi là quy tắc căn bậc hai của n (square root of n rule): để giảm sai số chuẩn đi một nửa, kích thước mẫu phải tăng gấp bốn lần.

Tính hợp lệ của công thức sai số chuẩn bắt nguồn từ định lý giới hạn trung tâm. Tuy nhiên, trên thực tế, không nhất thiết phải dựa vào định lý này để hiểu sai số chuẩn. Hãy xem xét cách tiếp cận sau để đo lường sai số chuẩn:

Thu thập nhiều mẫu hoàn toàn mới từ tổng thể.
Với mỗi mẫu mới, tính thống kê quan tâm (ví dụ: trung bình).
Tính độ lệch chuẩn của các thống kê thu được ở bước 2; giá trị này được dùng làm ước lượng của sai số chuẩn.

Trong thực tế, cách tiếp cận này—thu thập nhiều mẫu mới để ước lượng sai số chuẩn—thường không khả thi (và về mặt thống kê là rất lãng phí dữ liệu). May mắn thay, ta không cần phải rút các mẫu hoàn toàn mới; thay vào đó, ta có thể sử dụng các mẫu bootstrap. Trong thống kê hiện đại, bootstrap đã trở thành phương pháp chuẩn để ước lượng sai số chuẩn. Phương pháp này có thể áp dụng cho gần như mọi thống kê và không phụ thuộc vào định lý giới hạn trung tâm hay các giả định về phân phối khác.

Lưu ý là Không nên nhầm lẫn giữa:

Độ lệch chuẩn (standard deviation) — đo mức độ biến thiên của các điểm dữ liệu riêng lẻ, và
Sai số chuẩn (standard error) — đo mức độ biến thiên của một đại lượng thống kê mẫu.

**Ý chính của mục 3

Phân phối tần suất của một thống kê mẫu cho biết đại lượng đó có thể thay đổi như thế nào khi rút các mẫu khác nhau.
Phân phối lấy mẫu này có thể được ước lượng bằng bootstrap, hoặc bằng các công thức dựa trên định lý giới hạn trung tâm.
Một chỉ số quan trọng dùng để tóm tắt mức độ biến thiên của một thống kê mẫu là sai số chuẩn.

4. Bootstrap

Một cách đơn giản và hiệu quả để ước lượng phân phối lấy mẫu của một thống kê, hoặc của các tham số mô hình, là rút các mẫu bổ sung có hoàn lại từ chính mẫu ban đầu, rồi tính lại thống kê hoặc mô hình cho mỗi mẫu lấy lại đó. Quy trình này được gọi là bootstrap, và nó không nhất thiết phải giả định rằng dữ liệu hay thống kê mẫu tuân theo phân phối chuẩn.

Các thuật ngữ chính về Bootstrap

Bootstrap sample (Mẫu bootstrap):
Một mẫu được lấy có hoàn lại từ một tập dữ liệu đã quan sát.
Resampling (Lấy mẫu lại):
Quá trình lấy các mẫu lặp lại từ dữ liệu đã quan sát; bao gồm cả bootstrap và hoán vị (permutation/shuffling).

Về mặt khái niệm, có thể hình dung bootstrap như việc nhân bản mẫu gốc hàng nghìn hoặc hàng triệu lần, tạo ra một tổng thể giả định chứa toàn bộ thông tin từ mẫu ban đầu (chỉ khác là có kích thước lớn hơn). Từ tổng thể giả định này, ta có thể rút các mẫu nhằm ước lượng phân phối lấy mẫu.

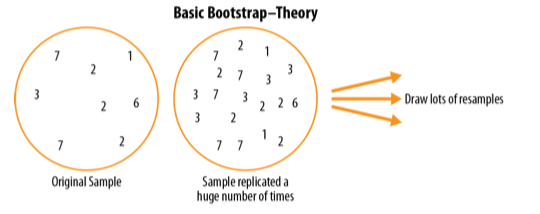
Trong thực tế, không cần phải thực sự sao chép mẫu gốc nhiều lần. Thay vào đó, ta hoàn lại mỗi quan sát sau mỗi lần rút; tức là lấy mẫu có hoàn lại. Bằng cách này, ta hiệu quả tạo ra một tổng thể vô hạn, trong đó xác suất để một phần tử được rút ra không thay đổi qua các lần rút.

Thuật toán bootstrap cho trung bình, với kích thước mẫu là n, được mô tả như sau:

Rút một giá trị từ mẫu, ghi nhận nó, rồi hoàn lại.
Lặp lại bước 1 n lần.
Tính trung bình của n giá trị được lấy.
Lặp lại các bước 1–3 R lần.
Sử dụng R kết quả thu được để:
a. Tính độ lệch chuẩn của chúng (ước lượng sai số chuẩn của trung bình mẫu).
b. Vẽ histogram hoặc boxplot.
c. Xác định khoảng tin cậy.

Số lần lặp R của bootstrap được chọn khá tùy ý. Lặp càng nhiều, ước lượng sai số chuẩn hoặc khoảng tin cậy càng chính xác. Kết quả của quy trình này là một tập các thống kê mẫu bootstrap hoặc các tham số mô hình được ước lượng, từ đó ta có thể xem xét mức độ biến thiên của chúng.

Gói boot trong R gộp các bước trên vào một hàm duy nhất. Ví dụ, đoạn mã sau áp dụng bootstrap cho thu nhập của những người vay vốn:

library(boot) stat_fun <- function(x, idx) median(x[idx]) boot_obj <- boot(loans_income, R = 1000, statistic = stat_fun)

Hàm stat_fun tính trung vị cho một mẫu được xác định bởi chỉ số idx. Kết quả có dạng:

Bootstrap Statistics : original bias std. error 62000 -70.5595 209.1515

Ước lượng trung vị ban đầu là 62.000 USD. Phân phối bootstrap cho thấy ước lượng này có độ chệch (bias) khoảng –70 USD và sai số chuẩn khoảng 209 USD. Kết quả sẽ thay đổi nhẹ giữa các lần chạy thuật toán.

Các thư viện Python phổ biến không cung cấp sẵn triển khai bootstrap. Tuy nhiên, có thể thực hiện bằng phương thức resample của scikit-learn:

results = [] for nrepeat in range(1000): sample = resample(loans_income) results.append(sample.median()) results = pd.Series(results) print('Bootstrap Statistics:') print(f'original: {loans_income.median()}') print(f'bias: {results.mean() - loans_income.median()}') print(f'std. error: {results.std()}')

Bootstrap có thể được áp dụng cho dữ liệu đa biến, trong đó mỗi hàng được lấy mẫu như một quan sát. Khi đó, ta có thể chạy một mô hình trên dữ liệu bootstrap để ước lượng độ ổn định (độ biến thiên) của các tham số mô hình, hoặc để cải thiện năng lực dự báo. Với cây phân loại và hồi quy (decision trees), việc chạy nhiều cây trên các mẫu bootstrap rồi lấy trung bình dự đoán (hoặc bỏ phiếu đa số với bài toán phân loại) thường cho kết quả tốt hơn so với dùng một cây đơn lẻ. Quy trình này được gọi là bagging. → Thuật toán Random Forest

Việc lấy mẫu lại lặp đi lặp lại trong bootstrap về mặt khái niệm tuy có vẻ đơn giản.

Nhà kinh tế học và nhân khẩu học Julian Simon đã công bố một tuyển tập các ví dụ về lấy mẫu lại, bao gồm bootstrap, trong cuốn Basic Research Methods in Social Science (1969).

Tuy nhiên, ngày xưa lúc máy móc phần cứng và năng lực tính toán còn hạn chế, kỹ thuật bootstrap được cho là đòi hỏi tính toán lớn và không khả thi. Kỹ thuật này được đặt tên và phát triển mạnh mẽ sau khi nhà thống kê học Bradley Efron (Stanford) công bố nhiều bài báo và một cuốn sách vào cuối thập niên 1970 và đầu thập niên 1980. Bootstrap đặc biệt phổ biến với các nhà nghiên cứu không chuyên thống kê, và trong các trường hợp không có sẵn xấp xỉ toán học cho các thước đo hay mô hình. Phân phối lấy mẫu của trung bình đã được thiết lập rõ ràng từ năm 1908; còn phân phối lấy mẫu của nhiều thước đo khác thì chưa. Bootstrap cũng có thể dùng để xác định kích thước mẫu (cỡ mẫu) (Cần bao nhiêu quan sát là đủ để làm thí nghiệm); bằng cách thử các giá trị khác nhau của n, ta có thể quan sát cách phân phối lấy mẫu thay đổi.

Nếu lấy n = 30, 50, 100…, thì độ bất định của kết quả thay đổi ra sao (SE càng nhỏ thì càng tốt)?

Khi mới được giới thiệu, bootstrap vấp phải nhiều hoài nghi; với nhiều người, nó giống như việc tạo ra những thông tin mới từ lượng dữ liệu hạn hẹp. Sự hoài nghi này bắt nguồn từ hiểu lầm về mục đích của bootstrap.

Bootstrap không bù đắp cho kích thước mẫu nhỏ; nó không tạo ra dữ liệu mới, cũng không lấp đầy các khoảng trống trong một tập dữ liệu hiện có. Bootstrap chỉ cho chúng ta biết: nếu ta có thể rút rất nhiều mẫu bổ sung từ một tổng thể ví dụ như mẫu ban đầu của chúng ta, thì các thống kê hay tham số mô hình sẽ biến thiên như thế nào.

Lấy mẫu lại (Resampling) so với Bootstrap

Đôi khi, thuật ngữ resampling (lấy mẫu lại) được dùng đồng nghĩa với bootstrapping, như đã trình bày ở trên. Tuy nhiên, trong nhiều ngữ cảnh, resampling được dùng với nghĩa rộng hơn, bao gồm cả các thủ tục hoán vị (permutation procedures), trong đó nhiều mẫu được kết hợp với nhau và việc lấy mẫu có thể được thực hiện không hoàn lại.

Dù sử dụng theo nghĩa nào, thuật ngữ bootstrap luôn mang ý nghĩa lấy mẫu có hoàn lại từ một tập dữ liệu đã quan sát.

Ý chính của mục số 4

Bootstrap (lấy mẫu có hoàn lại từ một tập dữ liệu) là một công cụ mạnh mẽ để đánh giá mức độ biến thiên của một thống kê mẫu.
Bootstrap có thể được áp dụng theo cùng một cách trong rất nhiều bối cảnh khác nhau, mà không cần nghiên cứu sâu các xấp xỉ toán học của phân phối lấy mẫu.
Bootstrap cho phép ước lượng phân phối lấy mẫu cho những thống kê chưa có xấp xỉ toán học được xây dựng.
Khi áp dụng cho mô hình dự báo, việc kết hợp (aggregate) các dự đoán từ nhiều mẫu bootstrap (bagging) cho kết quả tốt hơn so với việc sử dụng một mô hình đơn lẻ.

5. Khoảng tin cậy (Confidence Intervals)

Bảng tần suất, histogram, boxplot và sai số chuẩn đều là những cách giúp ta hiểu mức độ sai số tiềm ẩn trong một ước lượng từ mẫu. Khoảng tin cậy là một công cụ khác phục vụ cùng mục đích đó.

Các thuật ngữ chính về Khoảng tin cậy

Confidence level (Mức độ tin cậy):
Tỷ lệ phần trăm các khoảng tin cậy, được xây dựng theo cùng một cách từ cùng một tổng thể, mà dự kiến sẽ chứa giá trị thống kê quan tâm.
Interval endpoints (Cận dưới và cận trên):
Hai đầu trên và dưới của khoảng tin cậy.

Con người có xu hướng khó chấp nhận sự không chắc chắn; mọi người (đặc biệt là các chuyên gia) nói “tôi không biết” quá ít. Các nhà phân tích và nhà quản lý, dù thừa nhận sự bất định, vẫn thường đặt niềm tin quá mức vào một ước lượng khi nó được trình bày dưới dạng một con số duy nhất (ước lượng điểm). Trình bày kết quả dưới dạng một khoảng giá trị, thay vì một con số đơn lẻ, là một cách để hạn chế xu hướng này. Khoảng tin cậy thực hiện điều đó dựa trên các nguyên lý lấy mẫu thống kê.

Khoảng tin cậy luôn đi kèm với một mức độ bao phủ, được biểu diễn bằng một tỷ lệ phần trăm cao, chẳng hạn 90% hoặc 95%.

Ở đây chúng ta sẽ học cách ước lượng đại lượng thống kê dùng kỹ thuật Bootstrap thay vì truyền thống. Một cách để hiểu khoảng tin cậy 90% là: đó là khoảng bao phủ 90% phần trung tâm của phân phối lấy mẫu theo phương pháp bootstrap của một thống kê mẫu.

Tổng quát hơn, một khoảng tin cậy x% quanh một ước lượng mẫu, về trung bình, sẽ chứa các ước lượng mẫu tương tự x% số lần, khi cùng một quy trình lấy mẫu được áp dụng.

Với một mẫu có kích thước n và một thống kê mẫu quan tâm (ví dụ như mean), thuật toán xây dựng khoảng tin cậy bootstrap như sau:

Rút một mẫu ngẫu nhiên kích thước n, có hoàn lại, từ dữ liệu (một mẫu lấy lại).
Ghi nhận thống kê quan tâm (ví dụ như mean) cho mẫu lấy lại đó.
Lặp lại các bước 1–2 nhiều lần (R lần).
Đối với khoảng tin cậy x%, loại bỏ [(100−x)/2]% các kết quả bootstrap ở mỗi đầu của phân phối.
Hai điểm cắt sau khi loại bỏ chính là cận dưới và cận trên của khoảng tin cậy bootstrap x%.

Hình sau minh họa khoảng tin cậy 90% cho thu nhập trung bình hằng năm của các ứng viên vay vốn, dựa trên một mẫu gồm 20 quan sát, với trung bình mẫu là *62.231 USD.

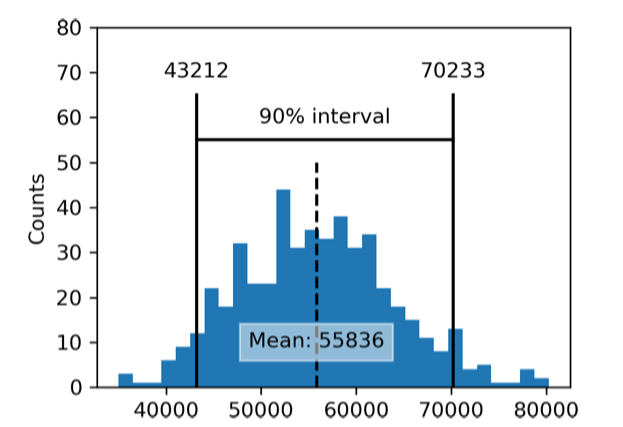
Bootstrap là một công cụ tổng quát, có thể dùng để xây dựng khoảng tin cậy cho hầu hết các thống kê hoặc tham số mô hình. Các giáo trình và phần mềm thống kê—vốn được phát triển từ thời kỳ phân tích thống kê chưa có máy tính—cũng thường đề cập đến các khoảng tin cậy được xây dựng bằng công thức, đặc biệt là dựa trên phân phối t. Nhược điểm của phương pháp truyền thống là để ước lượng chính xác chúng ta cần phải có các giả định như có trước phương sai tổng, nếu không có phương sai tổng thì phải giả định dữ liệu tuân theo phân phối chuẩn.

Nói như vậy không phải là Bootstrap không có điểm yếu, chúng ta có thể thấy Bootstrap sẽ phụ thuộc rất nhiều vào chất lượng của mẫu. Bootstrap yêu cầu giả định rằng Mẫu quan sát phải đại diện tốt cho tổng thể (vì thế nếu mẫu rất nhỏ hoặc không đại diện tốt thì thật ra cũng không quá tốt), tiếp theo là rõ ràng việc lấy mẫu Bootstrap và tính toán nhiều lần sẽ đánh đổi là chi phí tính toán cao.

Dĩ nhiên, khi có một kết quả từ mẫu, điều chúng ta thực sự quan tâm là:
“Xác suất để giá trị thực nằm trong một khoảng nhất định là bao nhiêu?”

Thực ra, đây không phải là câu hỏi mà khoảng tin cậy trả lời một cách trực tiếp, nhưng đó lại là cách mà đa số mọi người diễn giải kết quả.

Câu hỏi xác suất gắn với khoảng tin cậy thường bắt đầu bằng:

“Với một quy trình lấy mẫu và một tổng thể cho trước, xác suất để…”

Hoặc là

“Với một kết quả từ mẫu, xác suất để (đại lượng gì đó của tổng thể) là bao nhiêu?”

Việc này thật ra đòi hỏi các phép tính phức tạp hơn và liên quan đến những vấn đề sâu sắc, khó xác định.

Tỷ lệ phần trăm gắn với khoảng tin cậy được gọi là mức độ tin cậy. Mức độ tin cậy càng cao, thì khoảng tin cậy càng rộng. Đồng thời, kích thước mẫu càng nhỏ, thì khoảng tin cậy cũng càng rộng (tức là mức độ không chắc chắn càng lớn). Cả hai điều này đều hợp lý: bạn càng muốn chắc chắn hơn, và bạn càng có ít dữ liệu, thì khoảng tin cậy càng phải rộng để có thể bao phủ giá trị thực.

Đối với nhà khoa học dữ liệu, khoảng tin cậy là một công cụ giúp hình dung mức độ biến thiên có thể có của một kết quả từ mẫu. Nhà khoa học dữ liệu thường sử dụng thông tin này không phải để công bố bài báo học thuật hay nộp kết quả cho cơ quan quản lý (như các nhà nghiên cứu truyền thống), mà chủ yếu để truyền đạt mức độ sai số tiềm ẩn của một ước lượng, và có thể để đánh giá xem có cần thu thập thêm dữ liệu hay không.

Ý chính của mục 5 (Key Ideas)

Khoảng tin cậy là cách phổ biến để trình bày ước lượng dưới dạng một khoảng giá trị.
Càng có nhiều dữ liệu, ước lượng từ mẫu càng ít biến thiên.
Mức độ tin cậy càng thấp (bạn chấp nhận ít chắc chắn hơn), thì khoảng tin cậy càng hẹp.
Bootstrap là một phương pháp hiệu quả để xây dựng khoảng tin cậy.

6. Phân phối chuẩn (Normal Distribution)

Phân phối chuẩn có dạng đường cong hình chuông là một biểu tượng kinh điển trong thống kê truyền thống. Thực tế rằng phân phối của các thống kê mẫu thường có dạng gần giống phân phối chuẩn đã khiến nó trở thành một công cụ rất mạnh trong việc phát triển các công thức toán học dùng để xấp xỉ các phân phối này.

Các thuật ngữ chính liên quan đến phân phối chuẩn

Error (Sai số)
Sự khác biệt giữa một giá trị dữ liệu quan sát và một giá trị dự đoán hoặc giá trị trung bình.

Standardize (Chuẩn hóa)
Lấy giá trị dữ liệu trừ đi trung bình rồi chia cho độ lệch chuẩn.

z-score (Điểm z)
Kết quả của việc chuẩn hóa một giá trị dữ liệu riêng lẻ.

Standard normal (Phân phối chuẩn tắc)
Phân phối chuẩn có trung bình bằng 0 và độ lệch chuẩn bằng 1.

QQ-Plot
Biểu đồ dùng để trực quan hóa mức độ gần đúng giữa phân phối của mẫu và một phân phối cho trước, ví dụ như phân phối chuẩn.

Trong một phân phối chuẩn, 68% dữ liệu nằm trong khoảng một độ lệch chuẩn quanh giá trị trung bình, và 95% dữ liệu nằm trong khoảng hai độ lệch chuẩn quanh giá trị trung bình.

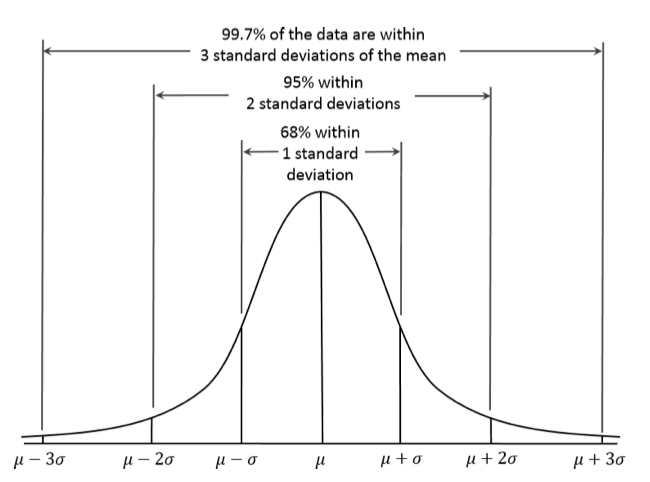
Một quan niệm sai lầm phổ biến là cho rằng phân phối chuẩn được gọi là “chuẩn” vì hầu hết dữ liệu đều tuân theo phân phối này — tức là đó là dạng “bình thường”. Trên thực tế, phần lớn các biến trong một dự án khoa học dữ liệu điển hình — thậm chí hầu hết dữ liệu thô — không tuân theo phân phối chuẩn.

Giá trị của phân phối chuẩn xuất phát từ thực tế rằng nhiều thống kê (statistics) lại tuân theo phân phối chuẩn trong phân phối lấy mẫu của chúng. Tuy vậy, các giả định về tính chuẩn thường chỉ được dùng như giải pháp cuối cùng, khi không có sẵn các phân phối xác suất thực nghiệm hoặc phân phối bootstrap.

Đường cong hình chuông tuy mang tính biểu tượng, nhưng có lẽ đã được đánh giá quá cao. George W. Cobb, một nhà thống kê học tại Mount Holyoke nổi tiếng với các đóng góp trong triết lý giảng dạy thống kê nhập môn, đã lập luận trong một bài xã luận tháng 11 năm 2015 trên tạp chí The American Statistician rằng: “Khóa học thống kê nhập môn tiêu chuẩn, đặt phân phối chuẩn làm trung tâm, đã không còn phù hợp với vai trò trung tâm đó nữa.”

Phân phối chuẩn còn được gọi là phân phối Gauss (Gaussian distribution), theo tên của Carl Friedrich Gauss — một nhà toán học kiệt xuất người Đức vào cuối thế kỷ 18 và đầu thế kỷ 19. Trước đây, phân phối chuẩn cũng từng được gọi là phân phối sai số (error distribution). Trong thống kê, sai số là sự khác biệt giữa giá trị thực tế và một ước lượng thống kê như trung bình mẫu. Ví dụ, độ lệch chuẩn được xây dựng dựa trên các sai số so với trung bình của dữ liệu. Việc Gauss phát triển phân phối chuẩn bắt nguồn từ nghiên cứu của ông về sai số trong các phép đo thiên văn, vốn được phát hiện là tuân theo phân phối chuẩn.

Phân phối chuẩn tắc (Standard Normal) và QQ-Plot

Phân phối chuẩn tắc là một phân phối chuẩn trong đó các đơn vị trên trục hoành (x-axis) được biểu diễn theo số độ lệch chuẩn so với giá trị trung bình. Để so sánh dữ liệu với phân phối chuẩn tắc, ta lấy mỗi giá trị trừ đi trung bình rồi chia cho độ lệch chuẩn; quá trình này còn được gọi là chuẩn hóa (normalization hoặc standardization) (xem “Standardization (Normalization, z-Scores)” ở trang 243). Lưu ý rằng “chuẩn hóa” theo nghĩa này không liên quan đến việc chuẩn hóa bản ghi trong cơ sở dữ liệu (tức chuyển dữ liệu về cùng một định dạng).

Giá trị sau khi biến đổi được gọi là z-score, và phân phối chuẩn đôi khi cũng được gọi là phân phối z (z-distribution).

QQ-Plot được sử dụng để đánh giá trực quan mức độ gần đúng giữa phân phối của một mẫu và một phân phối được chỉ định — trong trường hợp này là phân phối chuẩn. Trong QQ-Plot, các z-score được sắp xếp từ nhỏ đến lớn và mỗi z-score được vẽ trên trục tung (y-axis); trục hoành (x-axis) là phân vị tương ứng của phân phối chuẩn tại thứ hạng đó. Vì dữ liệu đã được chuẩn hóa, nên các đơn vị trên biểu đồ tương ứng với số độ lệch chuẩn so với trung bình.

Nếu các điểm dữ liệu xấp xỉ nằm trên đường chéo, ta có thể coi phân phối của mẫu là gần với phân phối chuẩn. Hình 2-11 minh họa một QQ-Plot cho một mẫu gồm 100 giá trị được sinh ngẫu nhiên từ phân phối chuẩn; đúng như kỳ vọng, các điểm bám rất sát đường chéo.

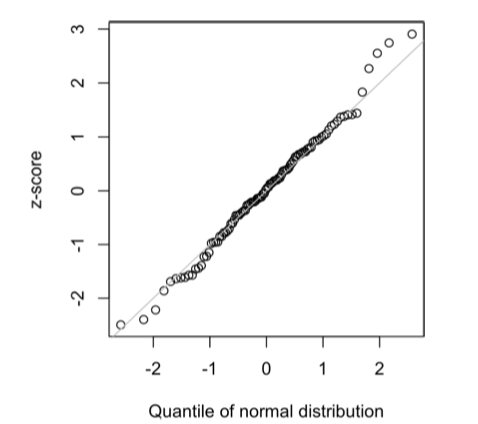
Trong Python, có thể sử dụng phương thức scipy.stats.probplot để tạo QQ-Plot:

fig, ax = plt.subplots(figsize=(4, 4)) norm_sample = stats.norm.rvs(size=100) stats.probplot(norm_sample, plot=ax)

Việc chuyển dữ liệu sang z-score (tức chuẩn hóa dữ liệu) không làm cho dữ liệu trở thành phân phối chuẩn. Nó chỉ đưa dữ liệu về cùng một thang đo với phân phối chuẩn tắc, chủ yếu nhằm mục đích so sánh.

Ví dụ ứng dụng: data drift trong production ML (Đọc thêm M06W3. 5 Grafana Prometheus for Tracking and Logging) Một kịch bản rất quen thuộc trong thực tế triển khai AI/ML là như sau:
mô hình của bạn được huấn luyện cẩn thận, validate ổn, deploy lên production và hoạt động rất tốt trong những tháng đầu. Các chỉ số như accuracy, AUC hay business KPI đều đạt kỳ vọng. Tuy nhiên, sau khoảng 4–6 tháng, hiệu năng bắt đầu suy giảm một cách âm thầm. Không có lỗi hệ thống, không có thay đổi code, nhưng mô hình đoán sai nhiều hơn.

Câu hỏi đầu tiên mà một data scientist cần đặt ra không phải là ""model có overfit không?”_, mà là:

Dữ liệu hiện tại còn giống dữ liệu dùng để huấn luyện mô hình hay không?

Đây chính là bài toán data drift / concept drift trong production ML.

Trong hệ thống thực tế, các feature thường có:

Đơn vị đo khác nhau (VNĐ, lần, phút, số ngày…)
Scale thay đổi theo thời gian (giá cả tăng, hành vi người dùng thay đổi)

Nếu so sánh trực tiếp giá trị thô giữa dữ liệu train và production, ta rất dễ bị đánh lừa bởi:

Lạm phát
Thay đổi sản phẩm
Thay đổi tập người dùng

Giải pháp hiệu quả là đưa mọi feature về cùng một hệ quy chiếu thống kê, và z-score làm rất tốt vai trò này.

Với mỗi feature, quy trình thường được thực hiện như sau:

Tính μ (mean) và σ (standard deviation) trên dữ liệu train
Chuẩn hóa dữ liệu train sang z-score
Chuẩn hóa dữ liệu production sang z-score, nhưng vẫn dùng μ, σ của train
Điều này rất quan trọng, vì ta đang hỏi:

“Dữ liệu mới đang lệch bao nhiêu so với thế giới mà mô hình từng biết?”
So sánh phân phối z-score giữa train và production, thay vì so sánh giá trị gốc.

Cách tính casio PP chuẩn

Phần hướng dẫn sau có thể giúp các bạn sau này đỡ phải đi tra bảng phân phối chuẩn mà chỉ cần bấm Casio

Chiều cao sinh viên có phân phối chuẩn $X \sim N (μ = 165, σ = 6)$ Tính xác suất một sinh viên cao dưới 170 cm. Cách bấm Casio

MENU
Chọn DIST
Chọn Normal CD
Nhập:
- Lower = -1E99
- Upper = 170
- μ = 165
- σ = 6
$P (X < 170) \approx 0.7977$

Bài 2: Tính xác suất sinh viên cao trên 180 cm. Cách bấm Casio

DIST → Normal CD

Lower = 180
Upper = 1E99
μ = 165
σ = 6
EXE

Bài 3: Xác suất sinh viên cao từ 160 cm đến 170 cm? DIST → Normal CD

Lower = 160
Upper = 170
μ = 165
σ = 6

Bài 4: Tìm chiều cao h sao cho 90% sinh viên thấp hơn h.

MENU
DIST
Normal PD
Nhập:
- Area = 0.9
- μ = 165
- σ = 6

Bài 5: Chuẩn hóa z-score Một sinh viên cao 175 cm, hỏi cao hơn bao nhiêu % sinh viên khác?

Chuẩn hóa: $z = \frac{175 - 165}{6} \approx 1.67$ DIST → Normal CD

Lower = -1E99
Upper = 1.67
μ = 0
σ = 1

$P (Z < 1.67) \approx 0.9525$

Ý chính mục 6

Phân phối chuẩn đóng vai trò then chốt trong lịch sử phát triển của thống kê vì nó cho phép xấp xỉ toán học đối với sự không chắc chắn và biến thiên.
Mặc dù dữ liệu thô thường không tuân theo phân phối chuẩn, nhưng sai số, cũng như trung bình và tổng trong các mẫu lớn, thường có dạng gần chuẩn.
Để chuyển dữ liệu sang z-score, ta lấy giá trị trừ trung bình rồi chia cho độ lệch chuẩn; từ đó có thể so sánh dữ liệu với phân phối chuẩn.

7. Phân phối đuôi dài (Long-Tailed Distributions)

Mặc dù phân phối chuẩn có vai trò rất quan trọng trong lịch sử thống kê, nhưng trái với ý nghĩa của cái tên, dữ liệu trong thực tế nói chung không tuân theo phân phối chuẩn.

Các thuật ngữ chính trong phân phối đuôi dài

Tail (đuôi)
Phần hẹp và kéo dài của phân phối tần suất, nơi các giá trị tương đối cực đoan xuất hiện với tần suất thấp.

Skew (độ lệch)
Hiện tượng một bên đuôi của phân phối dài hơn bên còn lại.

Trong khi phân phối chuẩn thường phù hợp và hữu ích khi mô tả phân phối của sai số hoặc phân phối của các thống kê mẫu, thì nó hiếm khi mô tả đúng phân phối của dữ liệu thô. Đôi khi, phân phối dữ liệu bị lệch mạnh (không đối xứng), ví dụ như dữ liệu thu nhập; hoặc phân phối có dạng rời rạc, như dữ liệu nhị phân (binomial). Cả phân phối đối xứng lẫn không đối xứng đều có thể có đuôi dài.

Phần đuôi của một phân phối tương ứng với các giá trị cực đoan (rất nhỏ hoặc rất lớn). Đuôi dài và việc phải cẩn trọng với chúng là điều được thừa nhận rộng rãi trong thực hành. Nassim Taleb đã đề xuất thuyết “Thiên nga đen” (black swan theory), theo đó các sự kiện bất thường — như sụp đổ thị trường chứng khoán — có khả năng xảy ra cao hơn nhiều so với những gì phân phối chuẩn dự đoán.

Lý thuyết Thiên Nga Đen do Nassim Nicholas Taleb đề xuất nhằm mô tả những sự kiện hiếm gặp nhưng có tác động cực lớn, thường không thể dự đoán bằng các mô hình thống kê truyền thống, đặc biệt là các mô hình giả định phân phối chuẩn.

Vì sao gọi là “Thiên Nga Đen”?

Trước thế kỷ 17, người châu Âu tin rằng mọi con thiên nga đều màu trắng.
Việc phát hiện thiên nga đen tại Úc đã phá vỡ một niềm tin tưởng chừng chắc chắn.
Ẩn dụ này cho thấy: chỉ một quan sát mới cũng đủ lật đổ một giả định lâu nay.

Ba đặc trưng cốt lõi của một Thiên Nga Đen

Tính hiếm (Rarity)
- Sự kiện rất ít khi xảy ra theo kinh nghiệm quá khứ.
- Các mô hình dựa trên dữ liệu lịch sử thường không dự báo được.
Tác động lớn (Extreme Impact)
- Khi xảy ra, hậu quả rất nghiêm trọng: tài chính, xã hội, công nghệ.
Hợp lý hóa sau sự kiện (Retrospective Rationalization)
- Sau khi sự kiện xảy ra, con người có xu hướng nói rằng
  “lẽ ra phải thấy trước”, dù trước đó không ai dự đoán được.

Ví dụ điển hình

Khủng hoảng tài chính toàn cầu 2008
Đại dịch COVID-19
Sự sụp đổ đột ngột của các tập đoàn lớn
Một nội dung mạng xã hội bùng nổ viral ngoài mọi dự đoán

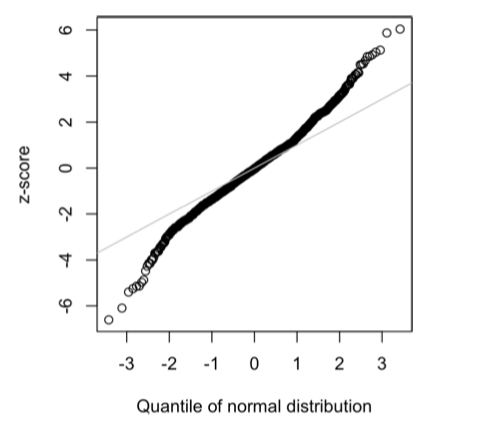
Một ví dụ điển hình để minh họa bản chất đuôi dài của dữ liệu là lợi suất cổ phiếu. Hình 2-12 cho thấy QQ-Plot của lợi suất cổ phiếu Netflix (NFLX) theo ngày.

nflx = sp500_px.NFLX
nflx = np.diff(np.log(nflx[nflx>0]))
 
fig, ax = plt.subplots(figsize=(4, 4))
stats.probplot(nflx, plot=ax)

Trái ngược với Hình ở Mục 6, các điểm trong QQ-Plot này nằm rất thấp so với đường chéo ở phía giá trị nhỏ và rất cao ở phía giá trị lớn, cho thấy dữ liệu không tuân theo phân phối chuẩn. Điều này có nghĩa là chúng ta có nhiều khả năng quan sát các giá trị cực đoan hơn so với trường hợp dữ liệu phân phối chuẩn.

Hình này còn cho thấy một hiện tượng phổ biến khác: các điểm dữ liệu gần với đường chéo trong khoảng một độ lệch chuẩn quanh giá trị trung bình. Tukey gọi hiện tượng này là dữ liệu “chuẩn ở phần giữa” (normal in the middle) nhưng có đuôi dài hơn nhiều (xem [Tukey-1987]).

Thảo luận: Có rất nhiều tài liệu thống kê bàn về việc khớp phân phối xác suất với dữ liệu quan sát được. Cần thận trọng với cách tiếp cận quá “lấy dữ liệu làm trung tâm”, bởi công việc này vừa là khoa học, vừa là nghệ thuật. Dữ liệu vốn biến thiên và thật ra thường có thể phù hợp với nhiều dạng và loại phân phối khác nhau. Do đó, kiến thức miền (domain knowledge) và kiến thức thống kê thường phải được kết hợp để xác định phân phối nào là phù hợp để mô hình hóa một tình huống cụ thể.

Ví dụ, nếu ta có dữ liệu về lưu lượng truy cập Internet trên một máy chủ được đo trong nhiều khoảng thời gian liên tiếp 5 giây, thì việc biết rằng phân phối phù hợp nhất để mô hình hóa “số sự kiện trên mỗi đơn vị thời gian” là phân phối Poisson sẽ rất hữu ích.

Ý chính của mục

Phần lớn dữ liệu không tuân theo phân phối chuẩn.
Việc giả định dữ liệu có phân phối chuẩn có thể dẫn đến đánh giá thấp các sự kiện cực đoan (“thiên nga đen”).

8. Phân phối t của Student (Student’s t-Distribution)

Phân phối t là một phân phối có dạng gần giống phân phối chuẩn, nhưng đuôi dày và dài hơn một chút. Phân phối này được sử dụng rất rộng rãi để mô tả phân phối của các thống kê mẫu. Phân phối của trung bình mẫu thường có dạng giống phân phối t, và thực tế tồn tại một họ các phân phối t khác nhau, phụ thuộc vào kích thước mẫu. Kích thước mẫu càng lớn thì phân phối t càng tiến gần tới phân phối chuẩn.

Các thuật ngữ chính trong phân phối t của Student

n Kích thước mẫu.

Bậc tự do (degrees of freedom) Một tham số cho phép phân phối t điều chỉnh theo kích thước mẫu, loại thống kê và số lượng nhóm.

Phân phối t thường được gọi là Student’s t vì nó được công bố năm 1908 trên tạp chí Biometrika bởi W. S. Gosset dưới bút danh “Student”. Chủ lao động của Gosset — hãng bia Guinness — không muốn đối thủ biết rằng họ đang sử dụng các phương pháp thống kê, nên yêu cầu Gosset không dùng tên thật khi xuất bản bài báo.

Gosset muốn trả lời câu hỏi:
“Phân phối lấy mẫu của trung bình một mẫu, được rút ra từ một tổng thể lớn hơn, là gì?”

Ông bắt đầu bằng một thí nghiệm tái lấy mẫu (resampling) — rút ngẫu nhiên các mẫu gồm 4 quan sát từ một tập dữ liệu gồm 3.000 phép đo chiều cao và chiều dài ngón tay giữa bên trái của tội phạm. (Vào thời điểm đó — kỷ nguyên của thuyết ưu sinh — người ta rất quan tâm đến dữ liệu về tội phạm và việc tìm mối liên hệ giữa xu hướng phạm tội với các đặc điểm thể chất hoặc tâm lý.) Gosset vẽ các kết quả đã được chuẩn hóa (z-score) trên trục hoành và tần suất trên trục tung. Song song đó, ông đã suy ra một hàm — ngày nay được gọi là phân phối t của Student — và khớp hàm này lên các kết quả mẫu để so sánh (xem Hình 2-13).

Nhiều loại thống kê khác nhau, sau khi được chuẩn hóa, có thể được so sánh với phân phối t để ước lượng khoảng tin cậy trong bối cảnh có biến thiên do lấy mẫu. Xét một mẫu kích thước n, với trung bình mẫu là x. Nếu s là độ lệch chuẩn mẫu, thì khoảng tin cậy 90% quanh trung bình mẫu được cho bởi:

$x \pm t_{n - 1, 0.05} \cdot \frac{s}{n}$

trong đó $t_{n - 1, 0.05}$ là giá trị thống kê t với $n - 1$ bậc tự do (xem Bậc tự do), giá trị này “cắt bỏ” 5% diện tích của phân phối t ở mỗi phía. Phân phối t đã được sử dụng như một chuẩn tham chiếu cho phân phối của trung bình mẫu, hiệu giữa hai trung bình mẫu, các tham số hồi quy và nhiều thống kê khác.

Quay lại với bàn luận lúc nãy về Ước lượng bằng Bootstrap Nếu năng lực tính toán đã phổ biến rộng rãi vào năm 1908, thì rất có thể thống kê học đã dựa nhiều hơn vào các phương pháp tái lấy mẫu tốn nhiều tính toán ngay từ đầu. Do thiếu máy tính, các nhà thống kê khi đó buộc phải dựa vào toán học và các hàm như phân phối t để xấp xỉ phân phối lấy mẫu. Đến những năm 1980, khi máy tính trở nên phổ biến, các thí nghiệm tái lấy mẫu mới thực sự khả thi trong thực tế; tuy nhiên, vào thời điểm đó, việc sử dụng phân phối t và các phân phối tương tự đã ăn sâu vào sách giáo khoa và phần mềm thống kê.

Độ chính xác của phân phối t trong việc mô tả hành vi của một thống kê mẫu đòi hỏi rằng phân phối của thống kê đó có dạng gần chuẩn. Thực tế cho thấy các thống kê mẫu thường có phân phối gần chuẩn, ngay cả khi dữ liệu của tổng thể ban đầu không tuân theo phân phối chuẩn — chính điều này đã dẫn đến việc phân phối t được ứng dụng rộng rãi. (Điều này lại đưa ta quay về hiện tượng được gọi là định lý giới hạn trung tâm)

Vậy các nhà khoa học dữ liệu cần biết gì về phân phối t và định lý giới hạn trung tâm? Không cần quá nhiều. Phân phối t đóng vai trò quan trọng trong suy luận thống kê cổ điển, nhưng không phải là trung tâm trong thực hành khoa học dữ liệu hiện đại. Việc hiểu và định lượng sự không chắc chắn và biến thiên vẫn rất quan trọng, nhưng bootstrap thực nghiệm có thể trả lời hầu hết các câu hỏi liên quan đến sai số do lấy mẫu. Tuy nhiên, các nhà khoa học dữ liệu sẽ thường xuyên gặp thống kê t trong đầu ra của phần mềm thống kê và các thủ tục thống kê trong R — chẳng hạn như trong A/B testing và hồi quy — vì vậy việc quen thuộc với mục đích của phân phối này là rất hữu ích.

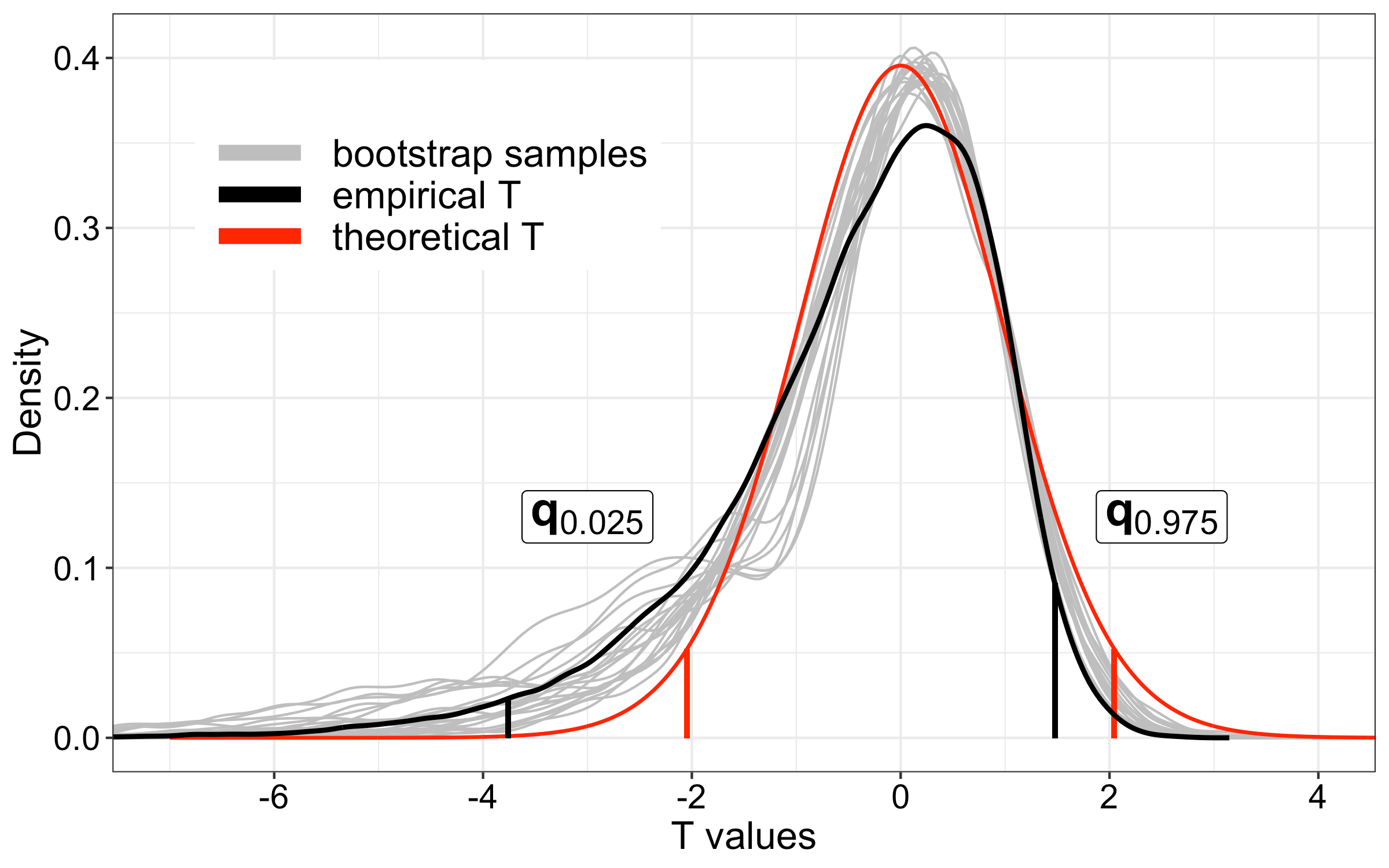
Các đường xám:
→ Phân phối các thống kê t từ từng mẫu bootstrap
(mỗi đường xám là một bootstrap resample)
Đường đen (empirical T):
→ Phân phối lấy mẫu thực nghiệm, được tổng hợp từ các bootstrap samples
→ Có thể hiểu là ước lượng trơn (smoothed estimate) của sampling distribution dựa trên bootstrap
Đường đỏ (theoretical T):
→ Phân phối t lý thuyết (Student’s t), tính bằng công thức

Ý chính của mục

Phân phối t thực chất là một họ các phân phối có hình dạng giống phân phối chuẩn nhưng đuôi dày hơn.
Phân phối t được sử dụng rộng rãi làm cơ sở tham chiếu cho phân phối của trung bình mẫu, chênh lệch giữa hai trung bình mẫu, các tham số hồi quy và nhiều thống kê khác.

9. Phân phối nhị thức (Binomial Distribution)

Các kết quả dạng có/không (yes/no) — hay còn gọi là nhị thức — nằm ở trung tâm của phân tích dữ liệu, vì chúng thường là kết quả cuối cùng của một quyết định hoặc một quá trình nào đó: mua/không mua, click/không click, sống/chết, v.v. Trọng tâm để hiểu phân phối nhị thức là khái niệm về một tập các phép thử, trong đó mỗi phép thử chỉ có hai kết quả có thể xảy ra, với xác suất xác định.

Ví dụ, việc tung đồng xu 10 lần là một thí nghiệm nhị thức với 10 phép thử, mỗi phép thử có hai kết quả khả dĩ (sấp hoặc ngửa); xem Hình 2-14. Những kết quả dạng có/không hoặc 0/1 như vậy được gọi là kết quả nhị phân (binary outcomes), và chúng không nhất thiết phải có xác suất 50/50. Bất kỳ cặp xác suất nào có tổng bằng 1.0 đều có thể xảy ra. Theo quy ước trong thống kê, kết quả “1” thường được gọi là kết quả thành công (success); đồng thời, cũng rất phổ biến khi gán “1” cho kết quả hiếm hơn. Việc dùng từ “thành công” không hàm ý rằng kết quả đó là tốt hay có lợi, mà chỉ nhằm chỉ ra kết quả mà ta quan tâm. Ví dụ, vỡ nợ khoản vay hoặc giao dịch gian lận là những sự kiện tương đối hiếm nhưng lại là đối tượng mà ta muốn dự đoán, nên chúng được gán là “1” hoặc “success”.

Các thuật ngữ chính trong phân phối nhị thức

Trial (phép thử)
Một sự kiện có kết quả rời rạc (ví dụ: tung đồng xu).

Success (thành công)
Kết quả mà ta quan tâm trong một phép thử.
Đồng nghĩa: “1” (đối lập với “0”).

Binomial (nhị thức)
Có hai kết quả.
Đồng nghĩa: yes/no, 0/1, nhị phân.

Binomial trial (phép thử nhị thức)
Một phép thử có hai kết quả.
Đồng nghĩa: phép thử Bernoulli.

Binomial distribution (phân phối nhị thức)
Phân phối của số lần thành công trong x phép thử.
Đồng nghĩa: phân phối Bernoulli.

Phân phối nhị thức là phân phối tần suất của số lần thành công (x) trong n phép thử, với xác suất thành công p cho mỗi phép thử. Tồn tại một họ các phân phối nhị thức, tùy thuộc vào giá trị của n và p. Phân phối nhị thức có thể trả lời những câu hỏi như:

Nếu xác suất một lượt click chuyển đổi thành mua hàng là 0,02, thì xác suất quan sát được 0 đơn hàng trong 200 lượt click là bao nhiêu?

Trong Python, mô-đun scipy. Stats triển khai nhiều phân phối thống kê. Đối với phân phối nhị thức, ta dùng các hàm stats. Binom. Pmf và stats. Binom. Cdf:

stats.binom.pmf(2, n=5, p=0.1) stats.binom.cdf(2, n=5, p=0.1)

Hàm này trả về giá trị 0,0729 — tức là xác suất quan sát đúng x = 2 lần thành công trong 5 phép thử, khi xác suất thành công của mỗi phép thử là p = 0,1. Với ví dụ ở trên, ta dùng x = 0, size = 200, và p = 0,02. Khi đó, dbinom trả về xác suất 0,0176.

Thông thường, ta quan tâm đến xác suất có x hoặc ít hơn x lần thành công trong n phép thử. Trong trường hợp này, ta dùng hàm

Hàm này trả về 0,9914, tức là xác suất quan sát không quá 2 lần thành công trong 5 phép thử, với xác suất thành công mỗi phép thử là 0,1.

Cách tính Casio Tỷ lệ chuyển đổi p = 0.02, số lượt click n = 200. Tính xác suất đúng 0 đơn hàng: $X \sim Bin (200, 0.02), P (X = 0)$

Cách bấm Casio (menu DIST)

MENU
Chọn DIST
Chọn Binomial
Chọn Bpd (Binomial Probability Distribution – PMF)

Nhập lần lượt:

x = 0
n = 200
p = 0.02

Nhấn = Máy trả về $P (X = 0) \approx 0.0176$

Xác suất tích lũy nhị thức — CDF Tính xác suất không quá 2 đơn hàng: $P (X \leq 2)$

MENU
DIST
Binomial
Bcd (Binomial Cumulative Distribution – CDF)

Nhập:

x = 2
n = 200
p = 0.02

Nhấn =

Máy trả về: $P (X \leq 2) \approx 0.991$

Giá trị trung bình của phân phối nhị thức là n × p; bạn cũng có thể hiểu đây là số lần thành công kỳ vọng trong n phép thử, với xác suất thành công p.

Phương sai của phân phối nhị thức là n × p × (1 − p). Khi số phép thử đủ lớn (đặc biệt khi p gần 0,5), phân phối nhị thức gần như không thể phân biệt được với phân phối chuẩn. Trên thực tế, việc tính toán xác suất nhị thức với kích thước mẫu lớn là tốn kém về mặt tính toán, nên hầu hết các thủ tục thống kê sử dụng phân phối chuẩn với cùng trung bình và phương sai để xấp xỉ.

Ý chính của mục

Các kết quả nhị thức rất quan trọng để mô hình hóa, vì chúng đại diện cho những quyết định cơ bản (mua hay không mua, click hay không click, sống hay chết, v.v.).
Một phép thử nhị thức là một thí nghiệm có hai kết quả: một với xác suất p và một với xác suất 1 − p.
Khi n đủ lớn và p không quá gần 0 hoặc 1, phân phối nhị thức có thể được xấp xỉ bằng phân phối chuẩn.

10. Phân phối Chi-bình phương (Chi-Square Distribution)

Một ý tưởng quan trọng trong thống kê là mức độ sai lệch so với kỳ vọng, đặc biệt trong các bài toán liên quan đến số lượng (count) theo từng nhóm/loại. Ở đây, kỳ vọng được hiểu một cách khái quát là “không có điều gì bất thường hay đáng chú ý trong dữ liệu” (ví dụ: không có mối tương quan giữa các biến, không có mô hình hay khuynh hướng có thể dự đoán được). Cách diễn đạt này cũng thường được gọi là giả thuyết không (null hypothesis) hoặc mô hình không (null model) (Sẽ được nhắc đến ở bài Kiểm định giả thuyết sau).

Ví dụ, kiểm tra xem một biến (chẳng hạn biến hàng biểu diễn giới tính) có độc lập với một biến khác (chẳng hạn biến cột biểu diễn việc có được thăng chức hay không) hay không, khi có bảng đếm số lượng quan sát trong từng ô của bảng dữ liệu. Thống kê dùng để đo lường mức độ mà kết quả quan sát được sai lệch so với kỳ vọng độc lập theo giả thuyết không chính là thống kê chi-bình phương (chi-square statistic).

Thống kê chi-bình phương được tính bằng cách lấy chênh lệch giữa giá trị quan sát và giá trị kỳ vọng, chia cho căn bậc hai của giá trị kỳ vọng, rồi bình phương, sau đó cộng lại trên tất cả các nhóm. Quy trình này giúp chuẩn hóa thống kê, để nó có thể được so sánh với một phân phối tham chiếu. Nói một cách tổng quát hơn, thống kê chi-bình phương đo lường mức độ mà một tập giá trị quan sát “phù hợp” với một phân phối đã được giả định trước — đây chính là một dạng kiểm định độ phù hợp (goodness-of-fit test). Nó đặc biệt hữu ích khi cần xác định xem nhiều phương án xử lý (ví dụ một bài toán A/B/C… test) có tạo ra các tác động khác nhau hay không.

Phân phối chi-bình phương là phân phối của thống kê này khi ta **lặp đi lặp lại việc lấy mẫu từ null model.

Giá trị chi-bình phương nhỏ cho thấy các số đếm quan sát được phù hợp khá sát với phân phối kỳ vọng.
Giá trị chi-bình phương lớn cho thấy các số đếm đó khác biệt đáng kể so với những gì ta kỳ vọng.

Tồn tại nhiều phân phối chi-bình phương khác nhau, tương ứng với các bậc tự do (degrees of freedom) khác nhau (sẽ được giới thiệu ở bài sau).

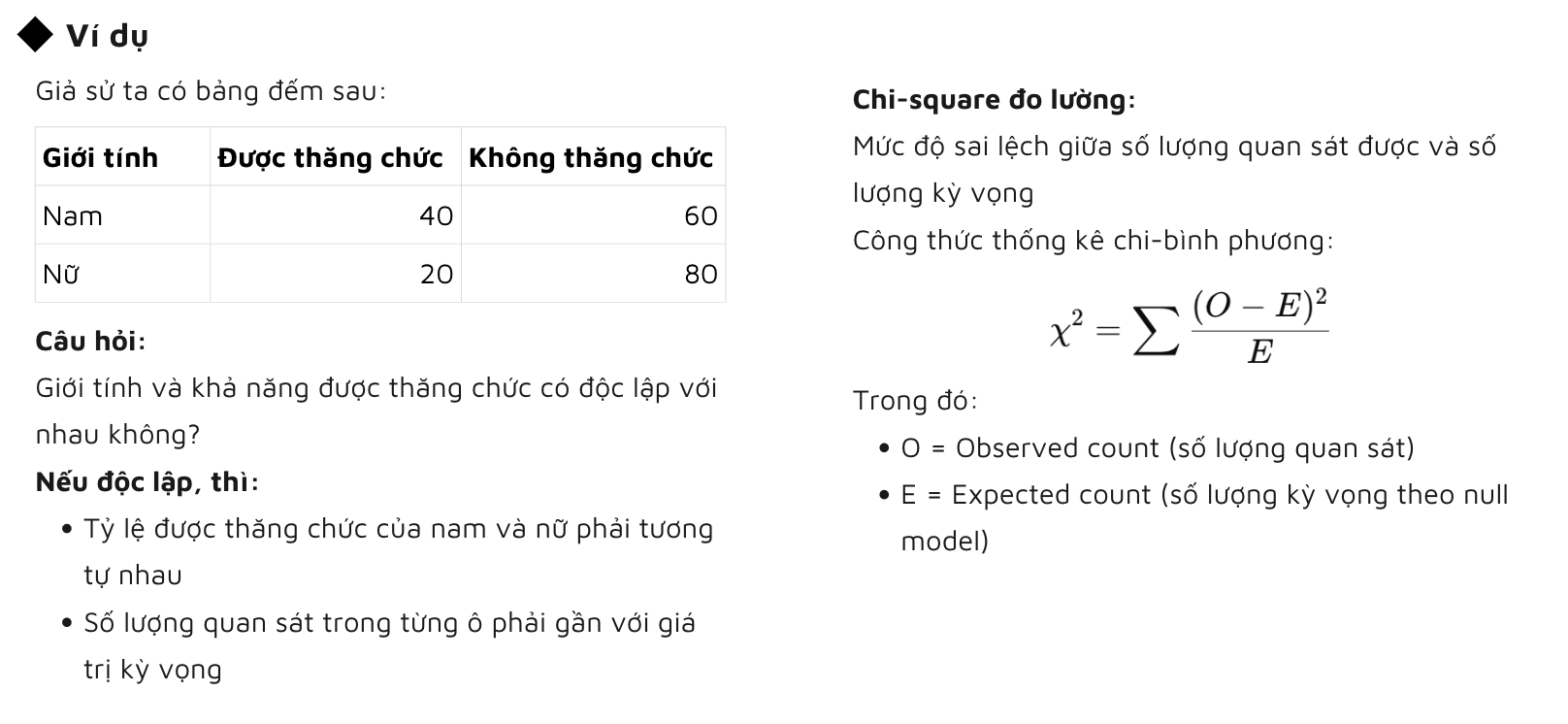Ý nghĩa của công thức

Lấy chênh lệch giữa quan sát và kỳ vọng
Chuẩn hóa bằng cách chia cho

EEE
Bình phương để:
- loại bỏ dấu âm
- phạt mạnh các sai lệch lớn
Cộng trên tất cả các ô

→ Ta thu được một con số duy nhất đo mức độ “không phù hợp” với null model.

Diễn giải giá trị Chi-square

χ2\chi^2χ2

nhỏ
→ Dữ liệu quan sát phù hợp tốt với kỳ vọng
→ Không có bằng chứng rõ ràng chống lại giả thuyết không
χ2\chi^2χ2

lớn
→ Sai lệch giữa quan sát và kỳ vọng rất lớn
→ Có dấu hiệu cho thấy:
- các biến không độc lập
- hoặc mô hình giả định không đúng

6. Phân phối Chi-square là gì?

Phân phối chi-bình phương là:

Phân phối của thống kê

χ2\chi^2χ2

khi ta lặp đi lặp lại việc lấy mẫu từ null model

Nói cách khác:

Nếu thế giới thật sự không có hiệu ứng
Nhưng ta lấy mẫu ngẫu nhiên nhiều lần
Thì các giá trị

χ2\chi^2χ2

thu được sẽ phân bố theo chi-square distribution

Ý chính của mục này

Phân phối chi-bình phương thường được dùng cho các bài toán liên quan đến số lượng đối tượng hoặc phần tử rơi vào các nhóm phân loại.
Thống kê chi-bình phương đo lường **mức độ sai lệch so với những gì ta mong đợi theo Null model.

11. Phân phối F (F-Distribution)

Một quy trình phổ biến trong các thí nghiệm khoa học là kiểm tra nhiều phương án xử lý (treatments) trên các nhóm khác nhau — chẳng hạn như so sánh các loại phân bón khác nhau trên các thửa ruộng khác nhau. Điều này tương tự với các bài toán A/B/C test được đề cập trong phân phối chi-bình phương, ngoại trừ việc ở đây ta làm việc với các giá trị đo liên tục, thay vì số đếm.

Trong bối cảnh này, điều ta quan tâm là mức độ mà sự khác biệt giữa các giá trị trung bình của các nhóm lớn hơn mức ta có thể kỳ vọng do dao động ngẫu nhiên thông thường. Thống kê F (F-statistic) được dùng để đo lường điều đó, và nó được định nghĩa là tỷ số giữa độ biến thiên giữa các trung bình nhóm và độ biến thiên bên trong từng nhóm (còn gọi là độ biến thiên dư, residual variability).

Sự so sánh này được gọi là phân tích phương sai (ANOVA). Phân phối của thống kê F là phân phối tần suất của tất cả các giá trị có thể thu được nếu ta hoán vị ngẫu nhiên dữ liệu trong trường hợp tất cả các trung bình nhóm đều bằng nhau (tức là theo mô hình không, null model). Tồn tại nhiều phân phối F khác nhau, tương ứng với các bậc tự do khác nhau.

Cách tính thống kê F có thể sẽ được minh họa chi tiết vào tuần sau trong phần ANOVA.

Ngoài ra, thống kê F còn được sử dụng trong hồi quy tuyến tính, để so sánh phần biến thiên được mô hình hồi quy giải thích với tổng biến thiên của dữ liệu. Trong thực tế, các giá trị F-statistic thường được tự động tạo ra bởi R và Python như một phần của các quy trình hồi quy và ANOVA.

Ý chính

Phân phối F được sử dụng trong các thí nghiệm và mô hình tuyến tính liên quan đến dữ liệu đo lường liên tục.
Thống kê F so sánh độ biến thiên do các yếu tố quan tâm gây ra với tổng độ biến thiên của dữ liệu.

11. Phân phối Poisson và các phân phối liên quan

Nhiều quá trình trong thực tế tạo ra các sự kiện xảy ra ngẫu nhiên với một tốc độ trung bình xác định — chẳng hạn như khách truy cập vào một website, hay xe cộ đi vào trạm thu phí (các sự kiện phân bố theo thời gian); hoặc các lỗi trên một mét vuông vải, hay số lỗi đánh máy trên mỗi 100 dòng mã (các sự kiện phân bố theo không gian).

Các thuật ngữ chính trong phân phối Poisson và các phân phối liên quan

Lambda (λ)
Tốc độ (trên mỗi đơn vị thời gian hoặc không gian) mà các sự kiện xảy ra.

Phân phối Poisson (Poisson distribution)
Phân phối tần suất của số sự kiện xảy ra trong các đơn vị thời gian hoặc không gian được lấy mẫu.

Phân phối mũ (Exponential distribution)
Phân phối tần suất của thời gian hoặc khoảng cách từ một sự kiện đến sự kiện kế tiếp.

Phân phối Weibull (Weibull distribution)
Một dạng tổng quát của phân phối mũ, trong đó tốc độ xảy ra sự kiện được phép thay đổi theo thời gian.

Phân phối Poisson

Từ dữ liệu tổng hợp trong quá khứ (ví dụ: số ca nhiễm cúm mỗi năm), ta có thể ước lượng số sự kiện trung bình trên mỗi đơn vị thời gian hoặc không gian (chẳng hạn: số ca nhiễm mỗi ngày, hoặc trên mỗi đơn vị điều tra dân số). Ta cũng có thể muốn biết mức độ biến thiên của số sự kiện này giữa các đơn vị thời gian/không gian khác nhau.

Phân phối Poisson cho ta biết phân phối của số sự kiện trên mỗi đơn vị thời gian hoặc không gian khi ta lấy mẫu nhiều đơn vị như vậy. Nó đặc biệt hữu ích trong các bài toán xếp hàng (queuing), chẳng hạn như:

“Cần bao nhiêu năng lực xử lý để có 95% chắc chắn rằng ta xử lý hết lưu lượng Internet đến một máy chủ trong bất kỳ khoảng 5 giây nào?”

Tham số quan trọng nhất của phân phối Poisson là λ (lambda). Đây là số sự kiện trung bình xảy ra trong một khoảng thời gian hoặc không gian xác định. Phương sai của phân phối Poisson cũng bằng λ.

Một kỹ thuật phổ biến là sinh các số ngẫu nhiên theo phân phối Poisson để phục vụ cho các mô phỏng xếp hàng. Trong Python (thư viện scipy) là stats.poisson.rvs:

stats.poisson.rvs(2, size = 100)

Đoạn mã này sẽ sinh ra 100 số ngẫu nhiên từ phân phối Poisson với λ = 2. Ví dụ, nếu số cuộc gọi vào bộ phận chăm sóc khách hàng trung bình là 2 cuộc mỗi phút, thì đoạn mã trên sẽ mô phỏng 100 phút, và trả về số cuộc gọi trong từng phút của 100 phút đó.

Ví dụ tính Casio

Trung bình một tổng đài nhận 1 = 2 cuộc gọi mỗi phút (Poisson). Tính:

P (X = 3): đúng 3 cuộc/phút
P (X ≤ 3): tối đa 3 cuộc/phút
P (X > 4): ít nhất 4 cuộc/phút
Trung bình 2 cuộc/phút, hỏi $P (X \leq 8 cuộc trong 5 ph \overset{u}{ˊ} t)$ .

Câu 1:

Vào: DIST → Poisson → Poisson PD
Nhập:
- x = 3
- λ = 2 Câu 2:
Vào: DIST → Poisson → Poisson CD
Nhập:
- x = 3
- λ = 2

Câu 3: • Tính P (X ≤ 3) như (2) • Sau đó bấm: • 1- Ans → ra P (X ≥ 4)

Câu 4: $λ_{5 ph \overset{u}{ˊ} t} = 2 \times 5 = 10$

Dùng Poisson CD
Nhập:
- x = 8
- λ = 10

Phân phối mũ (Exponential Distribution)

Sử dụng cùng tham số λ như trong phân phối Poisson, ta cũng có thể mô hình hóa phân phối của thời gian giữa các sự kiện: chẳng hạn thời gian giữa các lượt truy cập website, hoặc giữa các xe đến trạm thu phí. Phân phối này cũng được dùng trong kỹ thuật để mô hình hóa thời gian đến khi hỏng hóc, và trong quản lý quy trình để mô hình hóa, ví dụ, thời gian xử lý cho mỗi cuộc gọi dịch vụ.

Hàm stats.expon.rvs của Python (scipy)

stats.expon.rvs(0.2, size=100)

Đoạn mã này sẽ sinh 100 giá trị ngẫu nhiên từ một phân phối mũ trong đó tốc độ trung bình của các sự kiện là 0.2 trên mỗi đơn vị thời gian. Vì vậy, bạn có thể dùng nó để mô phỏng 100 khoảng thời gian (tính bằng phút) giữa các cuộc gọi dịch vụ, khi tốc độ trung bình của các cuộc gọi đến là 0.2 cuộc/phút.

Một giả định then chốt trong mọi nghiên cứu mô phỏng sử dụng phân phối Poisson hoặc phân phối mũ là tốc độ λ phải không đổi trong suốt khoảng thời gian được xét. Trên thực tế, giả định này hiếm khi đúng ở quy mô toàn cục; ví dụ, lưu lượng giao thông trên đường hoặc trên mạng dữ liệu thay đổi theo thời điểm trong ngày và theo ngày trong tuần. Tuy nhiên, ta thường có thể chia thời gian (hoặc không gian) thành các phân đoạn đủ đồng nhất, sao cho việc phân tích hoặc mô phỏng trong từng phân đoạn đó vẫn hợp lý và có giá trị.

Ước lượng tốc độ hỏng hóc (Estimating the Failure Rate)

Trong nhiều ứng dụng, tốc độ xảy ra sự kiện λ đã biết hoặc có thể ước lượng từ dữ liệu quá khứ. Tuy nhiên, đối với các sự kiện hiếm, điều này không hẳn đúng. Ví dụ, hỏng hóc động cơ máy bay là sự kiện đủ hiếm (may mắn là như vậy) đến mức, với một loại động cơ cụ thể, có thể rất ít dữ liệu để làm cơ sở ước lượng thời gian giữa các lần hỏng. Khi không có dữ liệu, gần như không có căn cứ để ước lượng tốc độ xảy ra sự kiện. Dẫu vậy, ta vẫn có thể đưa ra các phỏng đoán: chẳng hạn, nếu không quan sát thấy sự cố nào sau 20 giờ, ta có thể khá chắc rằng tốc độ không phải là 1 lần/giờ. Thông qua mô phỏng hoặc tính toán trực tiếp xác suất, ta có thể đánh giá các tốc độ giả định khác nhau và ước lượng các ngưỡng mà dưới đó tốc độ xảy ra sự kiện là rất khó có khả năng. Nếu có một ít dữ liệu nhưng chưa đủ để cung cấp một ước lượng chính xác và đáng tin cậy, có thể áp dụng kiểm định độ phù hợp (goodness-of-fit) (xem “Chi-Square Test” ở trang 124) cho các giá trị tốc độ khác nhau để xác định giá trị nào phù hợp nhất với dữ liệu quan sát.

Phân phối Weibull (Weibull Distribution)

Trong nhiều trường hợp, tốc độ xảy ra sự kiện không giữ nguyên theo thời gian. Nếu khoảng thời gian mà tốc độ thay đổi dài hơn nhiều so với khoảng cách điển hình giữa các sự kiện, thì không có vấn đề gì lớn; ta chỉ cần chia phân tích thành các đoạn mà trong đó tốc độ tương đối ổn định, như đã đề cập trước đó. Tuy nhiên, nếu tốc độ thay đổi ngay trong khoảng giữa các sự kiện, thì các phân phối mũ (exponential) hoặc Poisson không còn phù hợp. Điều này thường xảy ra trong hỏng hóc cơ khí—nguy cơ hỏng tăng dần theo thời gian.

Phân phối Weibull là phần mở rộng của phân phối mũ, trong đó tốc độ xảy ra sự kiện được phép thay đổi, được đặc tả bởi tham số hình dạng

Nếu β>1, xác suất xảy ra sự kiện tăng theo thời gian.
Nếu β<1, xác suất giảm theo thời gian.

Do Weibull được dùng cho phân tích thời gian đến hỏng hóc (time-to-failure) thay vì tốc độ sự kiện, tham số thứ hai được biểu diễn theo tuổi thọ đặc trưng, ký hiệu là η (chữ Hy Lạp eta), còn gọi là tham số tỷ lệ (scale parameter).

Với Weibull, bài toán ước lượng bao gồm hai tham số:

β và η

. Thông thường, phần mềm được sử dụng để mô hình hóa dữ liệu và ước lượng phân phối Weibull phù hợp nhất.

Trong Python, dùng hàm stats.weibull_min.rvs. Ví dụ, đoạn mã sau sinh 100 giá trị ngẫu nhiên (tuổi thọ) từ phân phối Weibull với shape = 1.5 và tuổi thọ đặc trưng = 5.000:

stats.weibull_min.rvs(1.5, scale=5000, size=100)

Ý chính của mục

Với các sự kiện xảy ra ở tốc độ không đổi, số sự kiện trên mỗi đơn vị thời gian hoặc không gian có thể được mô hình hóa bằng phân phối Poisson.
Thời gian hoặc khoảng cách giữa hai sự kiện liên tiếp có thể được mô hình hóa bằng phân phối mũ.
Khi tốc độ xảy ra sự kiện thay đổi theo thời gian (ví dụ, xác suất hỏng thiết bị tăng dần), có thể mô hình hóa bằng phân phối Weibull.

An Hoai Thai's Notes

Trong bài này

Buổi 3 Thống kê ứng dụng

Mở đầu: Dữ liệu và Phân phối mẫu

1. Lấy mẫu ngẫu nhiên và Sai lệch mẫu

Sai lệch (Bias)

Lựa chọn ngẫu nhiên (Random Selection)

Quy mô so với Chất lượng: Khi nào quy mô thực sự quan trọng?

Sample Mean Versus Population Mean (Trung bình mẫu và trung bình tổng thể)

Tổng hợp ý chỉnh của mục đầu tiên

2. Selection Bias (Sai lệch chọn mẫu / sai lệch lựa chọn)

Thuật ngữ chính về Selection Bias

Regression to the Mean (Hiện tượng hồi quy về trung bình)

Ý chính của mục hai

3. Phân phối lấy mẫu của một thống kê (Sampling Distribution of a Statistic)

Các thuật ngữ chính về phân phối lấy mẫu

Định lý Giới hạn Trung tâm

Sai số chuẩn(Standard Error)

**Ý chính của mục 3

4. Bootstrap

Lấy mẫu lại (Resampling) so với Bootstrap

Ý chính của mục số 4

5. Khoảng tin cậy (Confidence Intervals)

Ý chính của mục 5 (Key Ideas)

6. Phân phối chuẩn (Normal Distribution)

Phân phối chuẩn tắc (Standard Normal) và QQ-Plot

Cách tính casio PP chuẩn

Ý chính mục 6

7. Phân phối đuôi dài (Long-Tailed Distributions)

Vì sao gọi là “Thiên Nga Đen”?

Ba đặc trưng cốt lõi của một Thiên Nga Đen

Ví dụ điển hình

Ý chính của mục

8. Phân phối t của Student (Student’s t-Distribution)

Ý chính của mục

9. Phân phối nhị thức (Binomial Distribution)

Cách bấm Casio (menu DIST)

Ý chính của mục

10. Phân phối Chi-bình phương (Chi-Square Distribution)

6. Phân phối Chi-square là gì?

Ý chính của mục này

11. Phân phối F (F-Distribution)

Ý chính

11. Phân phối Poisson và các phân phối liên quan

Phân phối Poisson

Phân phối mũ (Exponential Distribution)

Ước lượng tốc độ hỏng hóc (Estimating the Failure Rate)

Phân phối Weibull (Weibull Distribution)

Ý chính của mục

Biểu Đồ

Bảng Nội Dung